Single Number & Single Number II

Single Number

题目链接：https://oj.leetcode.com/problems/single-number/

题意：给定一个整形数组，除一个元素外所有的元素都出现了两次，求该出现一次的元素。（能否不使用额外的内存）

思路：我们知道异或运算有以下特点：（1）满足交换律和结合率；（2）一个数异或自己结果为0，一个数异或0结果为自己

所以，将数组中的所有数异或后结果就是只出现一次的数。

代码：

class Solution {
public:
    int singleNumber(int A[], int n) {
        while(n-->1){
            A[0]^=A[n];
        }
        return A[0];
    }
};

Single Number II

题目链接：https://oj.leetcode.com/problems/single-number-ii/

题意：给定一个整形数组，除一个元素外所有的元素都出现了三次，求该出现一次的元素。（能否不使用额外的内存）

思路：从异或运算入手，一个int型的数有32位，我们暂时只考虑其中的一位（如下图所示），在整个数组中，该位含有的1和0的个数肯定都是3的倍数，最后多出一个0或者一个1。我们需要将这些0和1进行特定的异或运算后使其结果为多余的那个0或者1

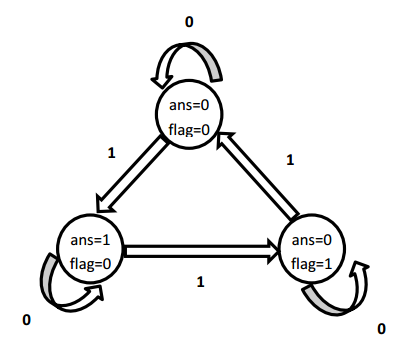
初步想法是初始值为0，然后一次处理每一位，如果该位为0，则结果不变，如果该位为1，则根据当前的结果进行变化，要达到的目的是接受3个1后，结果应该还原，接受一个1后结果为1，设置标志位进行标记。状态转移如下：

状态转移方程为：ans=(ans^A[i])&~flag      flag=(flag^A[i])&ans

每一位的处理方式都是一样的，所以将ans和flag转换为int型进行处理就可以得到结果了

代码如下：

class Solution {
public:
    int singleNumber(int A[], int n) {
        A[0]^=A[1];
        A[1]=(A[1]^A[0])&~A[0];
        while(n-->2){
            A[0]=(A[0]^A[n])&~A[1];
            A[1]=(A[1]^A[n])&~A[0];
        }
        return A[0];
    }
};

注意这一句：A[1]=(A[1]^A[n])&~A[0]; 和状态转移方程有点区别，程序中使用的是当前的ans（即A[0]），而方程中使用的是上一次的ans，所以在程序中对A[0]有一个取反的操作。