后缀数组 S A \tt SA SA 可以用于各方面字符串问题,其目的是求出这个字符串的所有后缀的按照字典序的排名。
前置知识
倍增 / DC3
算法用途
可以用来求最长公共子串,最长回文串等
算法复杂度
字符串长度为 n \tt n n
时间
O ( n log n ) \tt O(n\log n) O(nlogn)
空间
O ( n ) \tt O(n) O(n)
算法实现
要知道,最暴力算法就是把所有后缀找出来,然后用 s o r t \tt sort sort 排序
虽然时间复杂度和这个算法的优化版本一样 O ( n log n ) \tt O(n\log n) O(nlogn),但是这个算法的空间却是 O ( n 2 ) \tt O(n^2) O(n2) 的。很容易炸。
后缀数组需要求两个数组:后缀数组 S A \tt SA SA 和排名数组 r a n k \tt rank rank
S A i \tt SA_i SAi 代表从第 i \tt i i 个字符开始的后缀的排名。
r a n k i \tt rank_i ranki 代表排名为 i \tt i i 的后缀的开始字符的下标。
所以,其实 S A i = j \tt SA_i = j SAi=j 时, r a n k j = i \tt rank_j = i rankj=i。

对于后缀数组的实现,主要有两种算法:
-
倍增算法
-
DC3算法
我在这只讲倍增(主要是DC3我不会)。
倍增算法的思路主要是递推,
我们先求出每个后缀按照第一个字符的排序的 r a n k \tt rank rank(若第一个字符相同,则 r a n k \tt rank rank 相等),
即每个 i 对应的
S
[
i
,
i
]
S_{[i, i]}
S[i,i] 在所有
S
[
i
,
i
]
S_{[i, i]}
S[i,i] 中的排名。
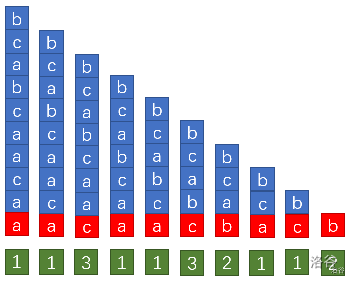
然后用所得出的 r a n k rank rank 来计算出所有后缀按照前两个字符排序的 r a n k \tt rank rank(每个 i \tt i i 对应的 S [ i , i + 2 0 ] \tt S_{[i, i+2^0]} S[i,i+20] 在所有 S [ i , i + 2 0 ] \tt S_{[i, i +2^0]} S[i,i+20] 中的排名。)
接着是四个,八个…,直到全部字符。(每个 i \tt i i 对应的 S [ i , i + 2 k ] \tt S_{[i, i+2^k]} S[i,i+2k] 在所有 S [ i , i + 2 k ] \tt S_{[i, i +2^k]} S[i,i+2k] 中的排名。)
过程如下:
假设我们要计算后缀按照前 2 k \tt 2^k 2k 个字符排序的 r a n k \tt rank rank。而我们已经求出了按前 2 k − 1 \tt 2^{k-1} 2k−1 个字符排序的 r a n k \tt rank rank。
那么对于每个 p \tt p p,我们要求的就是 S [ p , p + 2 k ] \tt S_{[p, p+2^{k}]} S[p,p+2k] 在所有 S [ i , i + 2 k ] \tt S_{[i, i+2^{k}]} S[i,i+2k] 的排名。
于是我们要考虑如何用 S [ i , i + 2 k − 1 ] \tt S_{[i, i + 2^{k-1}]} S[i,i+2k−1] 来表示 S [ p , p + 2 k ] \tt S_{[p, p+2^{k}]} S[p,p+2k]。
发现 S [ p , p + 2 k ] = S [ p , p + 2 k − 1 ] + S [ p + 2 k − 1 + 1 , p + 2 k ] \tt S_{[p, p+2^{k}]} = S_{[p, p+2^{k-1}]} + S_{[p+2^{k-1}+1, p+2^{k}]} S[p,p+2k]=S[p,p+2k−1]+S[p+2k−1+1,p+2k]。
而 S [ p , p + 2 k − 1 ] \tt S_{[p, p+2^{k-1}]} S[p,p+2k−1] 和 S [ p + 2 k − 1 + 1 , p + 2 k ] \tt S_{[p+2^{k-1}+1, p+2^{k}]} S[p+2k−1+1,p+2k] 的排名我们都已经求过了。
即 r a n k p \tt rank_p rankp, r a n k p + 2 k − 1 + 1 \tt rank_{p + 2^{k-1} +1} rankp+2k−1+1。
我们把所有
r
a
n
k
i
\tt rank_{i}
ranki 和
r
a
n
k
i
+
2
k
−
1
+
1
\tt rank_{i + 2^{k-1} +1}
ranki+2k−1+1 合并形成
n
\tt n
n 个二元组。

然后对于这个二元组排序,于是就可以得出新的 r a n k i \tt rank_i ranki。
重复这个步骤,直到所有 r a n k i \tt rank_i ranki 都不相同为止。然后求出来的 r a n k \tt rank rank 就是我们要求的排名数组的。

这时候,我们最多需要 log n \tt\log n logn 次求 r a n k \tt rank rank,每次求需要 O ( n log n ) \tt O(n\log n) O(nlogn) 的快速排序时间,所以总时间复杂度是 O ( n log 2 n ) \tt O(n\log^2n) O(nlog2n)。
算法应用
最长公共前缀(LCP)
S A \tt SA SA 数组还有一种基本操作,给两个后缀的开始字符串,求他们最长公共前缀长度。
我们可以快速求出排序后相邻两个字符串的最长公共前缀的长度。
我们让 h e i g h t i \tt height_i heighti 代表 S A i − 1 \tt SA_{i - 1} SAi−1 和 S A i \tt SA_i SAi 代表的两个后缀字符串的最长前缀的长度。
然后,我们可以得到两个后缀的排名 r a n k i , r a n k j \tt rank_i, rank_j ranki,rankj,然后我们只需要求出 min i + 1 ≤ x ≤ j ( h e i g h t i ) \tt \min_{i+1\leq x\leq j}(height_i) mini+1≤x≤j(heighti)
怎么求?只需要预处理然后使用 R M Q RMQ RMQ 就行了。
最长公共子串(LCS)
求 N \tt N N 个串的最长公共子串
我们发现这个问题可以转化为求一些后缀的最长公共前缀的最大值,这些后缀应分属于 N \tt N N 个串。
具体方法如下:
设 N \tt N N 个串分别为 S 1 , … , S N \tt S_1,…, S_N S1,…,SN,首先建立一个串 S \tt S S,把这 N \tt N N个串用不同的分隔符连接起来。 S = S 1 [ P 1 ] S 2 [ P 2 ] S 3 … S N − 1 [ P N − 1 ] S N \tt S = S_1[P_1]S_2[P_2]S_3…S_{N-1}[P_{N-1}]S_N S=S1[P1]S2[P2]S3…SN−1[PN−1]SN。
这些分隔符应为 N − 1 \tt N-1 N−1 个不在字符集中的字符。
接下来,求出字符串 S \tt S S 的后缀数组和 h e i g h t \tt height height 数组。
二分枚举答案 A \tt A A,于是问题就转化成 N \tt N N 个串是否可以有度为 A \tt A A 的公共字串,而代价是,我们多出来了一个 O ( log L ) \tt O(\log L) O(logL) 的时间复杂度。
如果能找出 h e i g h t height height 数组中连续的一段 [ i , j ] \tt [i,j] [i,j],满足排完序的后缀中第 [ i , j ] \tt [i, j] [i,j] 个后缀的起始字符分别属于 { S 1 , … , S n } \tt \{S_1,…,S_n\} {S1,…,Sn} 中的每个字符串,使得
min k ∈ [ i + 1 , j ] ( h e i g h t [ k ] ) > = A \tt \min_{k \in [i +1, j]}(height[k])>=A k∈[i+1,j]min(height[k])>=A
那么 A \tt A A 就是可行解,否则不是。
具体查找 [ i , j ] \tt [i, j] [i,j] 时,可以先从前到后枚举 i \tt i i 的位置,如果发现 h e i g h t i > = A \tt height_i>=A heighti>=A,则开始从 i \tt i i 向后枚举 j \tt j j 的位置,直到找到了 h e i g h t j + 1 < A \tt height_{j+1}<A heightj+1<A,判断是否满足上述情况。
如果满足,则 A \tt A A 为可行解,然后直接返回,否则令 i = j + 1 \tt i=j+1 i=j+1 继续向后枚举。
S \tt S S 中每个字符被访问了 O ( 1 ) \tt O(1) O(1) 次, S \tt S S 的长度为 N L + N − 1 \tt NL+N-1 NL+N−1,所以时间复杂度为 O ( N L ) \tt O(NL) O(NL)。
到这里,我们就可以理解为什么分隔符 P 1 . . P N − 1 \tt P_1..P_{N-1} P1..PN−1 必须是不同的 N − 1 \tt N-1 N−1 个不在字符集中的字符了,这样才能保证 S \tt S S 的后缀的公共前缀不会跨出一个原有串的范围。(当然你也可以用其他方法来避免)
算法优化
- 基数排序优化
我们知道,因为 r a n k \tt rank rank 数组里的数一定在 [ 1 , n ] \tt [1, n] [1,n] 的范围内,所以我们可以使用基数排序来代替快速排序。
二元组基数排序,我们需要先把第二关键字放进桶中,然后从小到大枚举每个桶,把桶里的数按照放进去的顺序挨个取出来,
再把第一关键字放进去,同样取出来,然后得到的数组就是排好序的了。
所以这个排序算法复杂度是 O ( n ) \tt O(n) O(n) 的,这样优化后的时间复杂度就是 O ( n log n ) \tt O(n\log n) O(nlogn) 了
代码
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char str[100010];
int cnt[100010];
int rk[100010];
int y[100010];
int SA[100010];
int height[100010];
int n, m;
int get_SA()
{
for(int i = 1; i <= n; i++)
{
rk[i] = str[i];
cnt[rk[i]]++;
}
for(int i = 2; i <= m; i++)
{
cnt[i] += cnt[i - 1];
}
for(int i = n; i >= 1; i--)
{
SA[cnt[rk[i]]--] = i;
}
for(int k = 1; k <= n; k <<= 1)
{
int num = 0;
for(int i = n - k + 1; i <= n; i++)
{
y[++num] = i;
}
for(int i = 1; i <= n; i++)
{
if(SA[i] > k)
{
y[++num] = SA[i] - k;
}
}
for(int i = 1; i <= m; i++)
{
cnt[i] = 0;
}
for(int i = 1; i <= n; i++)
{
cnt[rk[i]]++;
}
for(int i = 2; i <= m; i++)
{
cnt[i] += cnt[i - 1];
}
for(int i = n; i >= 1; i--)
{
SA[cnt[rk[y[i]]]--] = y[i];
y[i] = 0;
}
swap(rk, y);
rk[SA[1]] = 1;
num = 1;
for(int i = 2; i <= n; i++)
{
if(y[SA[i]] == y[SA[i - 1]] && y[SA[i] + k] == y[SA[i - 1] + k])
{
rk[SA[i]] = num;
}
else
{
rk[SA[i]] = ++num;
}
}
if (num == n)
{
break;
}
m = num;
}
for(int i = 1; i <= n; i++)
{
printf("%d ", rk[i]);
}
printf("\n");
}
void get_height()
{
for(int i = 1; i <= n; i++)
{
rk[SA[i]] = i;
}
int k = 0;
for(int i = 1; i <= n; i++)
{
if(k)
{
k--;
}
int j = SA[rk[i] - 1];
while(str[i + k] == str[j + k])
{
k++;
}
height[rk[i]] = k;
}
for(int i = 1; i <= n; i++)
{
printf("%d ", height[i]);
}
printf("\n");
}
int main()
{
scanf("%s", str + 1);
n = strlen(str + 1);
m = 256;
get_SA();
get_height();
return 0;
}





















 749
749











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








