最小二乘算法 Least Squares Algorithm

最新推荐文章于 2024-04-27 09:28:08 发布

Fally J 幻灵

最新推荐文章于 2024-04-27 09:28:08 发布

阅读量2.1k

点赞数 1

分类专栏：控制工程

本文链接：https://blog.csdn.net/FallyJ/article/details/115915819

版权

控制工程专栏收录该内容

3 篇文章 9 订阅

订阅专栏

引入

情景：假设我们想要用一个指标criterion 来衡量一个班学生的身高水平，现在想要选择这样一个具有代表性的指标，如何选取

学生测身高的图像结果

方法一：假设指标 c (criterion)可代表班级身高水平，那么指标与实际的误差可表示为

$f(x)=(x_{1}-c)+(x_{2}-c)+...(x_{n}-c)$

为了保证所选择的指标具有代表性，误差需要尽可能小，我们可以对 f(x) 进行求导判断，但是会发现，求导后的数据与 c 无关，误差完全取决于样本数据，这不是我们想要的。

方法二：在方法一的基础上，改变误差的表达式如下，它仍然表示指标与实际值的差距，只不过平方运算将原有差距进一步放大

$f(x)=(x_{1}-c)^{2}+(x_{2}-c)^{2}+...(x_{n}-c)^{2}$

我们用之前同样的方法，对 f(x) 进行求导，为了找到使误差最小时，指标 c 的表达式，我们令导数为零，可得结果如下

$c=\frac{x_{1}+x_{2}+...+x_{n}}{n}$

这眼熟的公式便是我们处理数据时常用的 平均值average，也称为期望expectation。经过上述的推理过程，我们之所以常用它来代表一个数据集的属性，也是因为它与实际数据的误差最小，而这个误差表达式 f(x) 也是我们常用的方差variance

一维递推最小二乘 one dimension RLS

有了上述的原理之后，我们将它的求取衍生出算法，提高它的实时处理能力。用求均值的方式，写出 t 时刻和 t+1 时刻的估计值

$\begin{align*} \left. \begin{align*} \hat{x}(t)&=\frac{1}{t}\sum_{i=1}^{t}{x(i)}\\ \hat{x}(t+1)&=\frac{1}{t+1}\sum_{i=1}^{t+1}{x(i)} \end{align*} \right \} \Rightarrow \hat{x}(t+1)&=\frac{t}{t+1}\hat{x}(t)+\frac{1}{t+1}x(t+1)\\ &=\hat{x}(t)+\frac{1}{t+1}[x(t+1)-\hat{x}(t)] \end{align*}$

这样，对于实时收集的数据，不用保存所有数据进行计算，只需要根据上一次计算的估计值estimation 和收集到的当前数据，便可以计算出新的估计值，可以有效的节省内存，提高运算效率。这种根据上次计算结果进行实时更新迭代的算法，称为 递推最小二乘Recursive Least Squares algorithm。中括号内的表达式称为新息innovation

二维最小二乘

现在，假设我们有一堆数据，是 n 个点的坐标数据(x和y)，我们希望通过这些数据，拟合出一条直线，能够尽可能的代表这些点的分布 (即散点图求拟合直线)。用最开始的方法，我们先假定一条最具代表性的直线 y=kx+b，那么现在我们需要做的，就是用最小二乘的方式，求得这条直线 (即两个参数 k 和 b)。

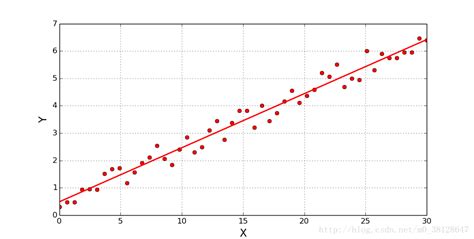
拟合直线的图像结果

类似于方差的定义，我们自定义函数 J 评判误差 (点到拟合线的距离)，并希望它能达到最小 (同样通过求导找极值点)

$\begin{align*} &if \ J(k,b)=\sum_{i=1}^{n}{(kx_{i}+b-y_{i})^{2}}\\ &let \left \{ \begin{align*} \frac{\partial J}{\partial k}&=2\sum_{i=1}^{n}{x_{i}(kx_{i}+b-y_{i})}&=0\\ \frac{\partial J}{\partial b}&=2\sum_{i=1}^{n}{kx_{i}+b-y_{i}}&=0 \end{align*} \right. &&\Rightarrow \sum_{i=1}^{n}{\left[ \begin{array} {cc} x_{i}^{2} & x_{i}\\ x_{i} & 1 \end{array} \right ] \left[ \begin{array} {cc} k\\b \end{array} \right ]}= \sum_{i=1}^{n}{ \left[ \begin{array} {cc} x_{i}\\ 1 \end{array} \right ]y_{i}} \end{align*}$

我们将表达式用矩阵表示，并取掉复杂的求和运算

$\begin{align*} &let \ \varphi_{i}=\left[ \begin{array}{cc} x_{i}\\1 \end{array} \right ],\theta=\left[ \begin{array}{cc} k\\b \end{array} \right ],then&&\Rightarrow (\sum_{i=1}^{n}{\varphi_{i}\varphi_{i}^{T}})\theta=\sum_{i=1}^{n}{\varphi_{i}y_{i}} \\ &let \ Y_{n}=\left[ \begin{array}{cccc} y_{1}\\y_{2}\\...\\y_{n} \end{array} \right ]\in \mathbb{R}^{n}, H_{n}=\left[ \begin{array}{cccc} \varphi_{1}^{T}\\\varphi_{2}^{T}\\...\\\varphi_{n}^{T} \end{array} \right ]\in \mathbb{R}^{n \times m} &&\Rightarrow \hat{\theta}=(H_{n}^{T}H_{n})^{-1}H_{n}^{T}Y_{n} \end{align*}$

很显然，H代表横坐标矩阵，Y代表纵坐标矩阵，所以，θ的估计值仅和坐标有关。所以，我们可以通过已有的坐标数据，求出相应的 k 和 b 值

最小二乘估计

针对上述 H 与 Y 的关系，将 H 看作输入，Y 看作输出，则系数矩阵 θ 表示了输入输出之间的关系。我们将这种关系的估算拓展到更高的维度，考虑多输入多输出(BIBO) 系统，且考虑系统在测得输入输出值时的误差 v (白噪声)

$\left \{ \begin{align*} y_{1}&=\theta_{11}x_{1}+\theta_{12}x_{2}+...+\theta_{1n}x_{n}+v_i(1)\\ y_{2}&=\theta_{21}x_{1}+\theta_{22}x_{2}+...+\theta_{2n}x_{n}+v_i(2)\\ &...\\ y_{m}&=\theta_{m1}x_{1}+\theta_{m2}x_{2}+...+\theta_{mn}x_{n}+v_i(n) \end{} \right.$

为了计算方便，将上述表达式简化为矩阵形式

$\begin{align*} \varphi(t)&=[x_{1}(t) \quad x_{2}(t) \quad ... \quad x_{n}(t)]\\ \Theta &= \left[ \begin{array} {cccc} \theta_{11} & \theta_{21} & ... & \theta_{m1} \\ \theta_{12} & \theta_{22} & ... & \theta_{m2} \\ ... & ... & &... \\ \theta_{1n} & \theta_{2n} & ... & \theta_{mn} \\ \end{} \right]\\ Y_{t} &= \left[ \begin{array} {cccc} y^{T}(1)\\ y^{T}(2) \\ ... \\ y^{T}(t)\\ \end{} \right], H_{t} = \left[ \begin{array} {cccc} \varphi^{T}(1)\\ \varphi^{T}(2) \\ ... \\ \varphi^{T}(t)\\ \end{} \right], V_{t} = \left[ \begin{array} {cccc} v^{T}(1)\\ v^{T}(2) \\ ... \\ v^{T}(t)\\ \end{} \right]\end{}$

接下来，用之前同样的方式写出误差标准函数(error criterion function)如下

$\begin{align*} J(\Theta)&=\sum_{k=1}^{n}\sum_{i=1}^{t}(y_{k}(i)-\varphi^{T}(i)\theta_{k})^{2}\\ &=(Y_t-H_t\Theta)^{T}(Y_t-H_t\Theta) \end{}$

由于此处是矩阵运算，所以，在求导找极值点之前，先引入两个矩阵导数公式： $\frac{\partial (x^{T}Ax)}{\partial x}=A^Tx+Ax,\quad \frac{\partial (Ax)}{\partial x}=A^T$

利用这两个求导公式，上述标准函数 J 对 Θ 求导可得

$\begin{align*} \frac{\partial J(\Theta)}{\partial \Theta}&=2(\frac{\partial (Y_t-H_t\Theta)}{\partial \Theta})(Y_t-H_t\Theta)\\ &=-2H_t(Y_t-H_t\Theta) \end{}$

为了找到最合适的 Θ，需要误差最小，此时 Θ 取极值点

$\begin{align*} \frac{\partial J(\Theta)}{\partial \Theta}&=0\\ H_tY_t&=H_t^{T}H_t\Theta\\ \hat{\Theta}_{LS}&=(H_t^TH_t)^{-1}H_t^TY_t \end{}$

可以发现，此处的结论，与二维算法非常相似，但是此处公式更为通用，阐释了 n 维输入与 m 维输出时，对系统参数的 最小二乘估计(Least Squares Estimation)

LSE的统计特性

期望

根据白噪声的特点，我们设白噪声的统计特性如下

$E[v(t)]=0,\quad E[v^2(t)]=\sigma ^2,\quad cov[V_t]=R_v=\sigma ^2 I_t$

那么，LSE满足如下关系

$\begin{align*} \hat{\theta}&=(H^T_tH_t)^{-1}H_t^TY_t\\ &=(H^T_tH_t)^{-1}H_t^T(H_t\theta+V_t)\\ &=\theta+(H^T_tH_t)^{-1}H_t^TV_t \end{}$

由于白噪声的期望为零，因此LSE的期望为

$\begin{align*} E\hat{\theta}&=E\theta+(H^T_tH_t)^{-1}H^T_t \cdot EV_t\\ &=\theta \end{}$

可见，LSE属于无偏估计

方差

令 $\tilde{\theta}=\hat{\theta}-\theta$ ,不难得其期望为零，其方差为

$\begin{align*} var \ \tilde{\theta}&=E(\tilde{\theta}\tilde{\theta}^T)\\ &=E[(H^T_tH_t)^{-1}H^T_tV_tV^T_tH_t(H^T_tH_t)^{-1}]\\ &=E[(H^T_tH_t)^{-1}H^T_t\cdot E(V_tV^T_t)\cdot H_t(H^T_tH_t)^{-1}]\\ &=\sigma^2E[(H^T_tH_t)^{-1}] \end{}$

误差标准函数

对于误差标准函数 J 满足

$\begin{align*} EJ&=E[(Y_t-H_t\hat{\theta})^T(Y_t-H_t\hat{\theta})]\\ &=E[tr(Y_t-H_t\hat{\theta})^T(Y_t-H_t\hat{\theta})]\\ &=tr[E(Y_t-H_t\hat{\theta})^T(Y_t-H_t\hat{\theta})]\\ \end{}$

上述利用矩阵迹(trace) 的规则进行变换，又

$\begin{align*} &\because H_t\hat{\theta}=H_t\theta+H_t(H^T_tH_t)^{-1}H^T_tV_t\xrightarrow[]{let\ H_t(H_t^TH_t)^{-1}H_t^T=Q}H_t\hat{\theta}=H_t\theta+QV_t\\ &\therefore \begin{align*} Y_t-H_t\hat{\theta}&=(H_t\theta+V_t)-(H_t\theta+QV_t)\\ &=(I_t-Q)V_t \end{} \end{}$

在这里引入 投影矩阵(idempotent matrix) 的概念，即一个矩阵转置后仍然是它本身，则该矩阵称为投影矩阵。不难得，此处的 Q 就是一个投影矩阵，则

$\dpi{100} \begin{align*} EJ&=tr\{E[(I_t-Q)V_tV_t^T(I_t-Q)^T]\}\\ &=tr[(I_t-Q)\sigma^2]\\ &=\sigma^2(t-dim(\theta)) \end{}$

Fally J 幻灵

关注

1
点赞
踩
11

收藏

觉得还不错? 一键收藏
0
评论
最小二乘算法 Least Squares Algorithm

引入情景：假设我们想要用一个指标criterion 来衡量一个班学生的身高水平，现在想要选择这样一个具有代表性的指标，如何选取方法一：假设指标 c (criterion)可代表班级身高水平，那么指标与实际的误差可表示为为了保证所选择的指标具有代表性，误差需要尽可能小，我们可以对 f(x) 进行求导判断，但是会发现，求导后的数据与 c 无关，误差完全取决于样本数据，这不是我们想要的。方法二：在方法一的基础上，改变误差的表达式如下，它仍然表示指标与实际值的差距，只不过平方运算将原有差距进一
复制链接

扫一扫