数据结构 三元组、矩阵、广义表 学习心得代码

0.前言：      

        用三元组储存稀疏矩阵，由于矩阵可表示为二维数组，下面的代码我将用二维数组表示矩阵，然后将矩阵储存到三元组。此处广义表主要是一些考虑深度和广度、表头表尾，其他内容在课上也是一笔带过（HEBUT），所以下面只会简单讲讲广义表。   

---

1.快速转置算法：

        矩阵转置中一个重要的算法就是基于三元组的快速转置算法，这个算法当时上课在讲的时候，博主一时有点摸不清脑瓜，下面我打算一步一步的来分析一下这个算法。

        这里是创建了两个一维数组，一个用来存放转置前三元组中每列（转置后三元组每行）的非零元的个数，另一个用来存放转置前三元组此列（转置后三元组行）第一个非零元的位置（类似于“首地址”的概念）。

for (col = 1;col<=M->nu;col++)    //置空一维数组num（每列/行的非零元）
    num[col] = 0;
for (int i = 1;i<=M->tu;i++)      //计算每列非零行数
    num[M->data[i].j]++;
cpot[1] = 1;                      //计算“首地址”
for(col = 2;col<=M->nu;col++)        
    cpot[col] = cpot[col - 1] + num[col - 1];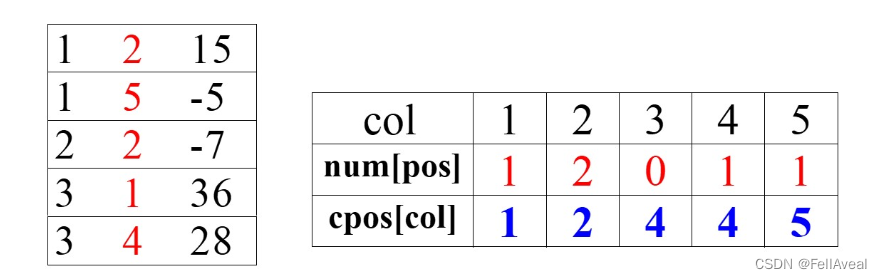

         下面就是转置的操作，遍历M的data，一个一个的转置入T三元组。cpot存的是某列第一个非零元应存到的位置，当存入一个之后，进行加一操作，方便该列第二个非零元进入。其余就是存入行和列、元素的内容。

for(int p = 1;p<=M->tu;p++){
    col = M->data[p].j;
    q = cpot[col];
    T->data[q].i = M->data[p].j;
    T->data[q].j = M->data[p].i;
    T->data[q].e = M->data[p].e;
    cpot[col]++;

---

 2.三元组与矩阵代码综合展示（不含矩阵乘法）：

//
// Created by DDD on 2023/11/6.
//
#include <stdio.h>

#define MAXSIZE 80
#define ARRSIZE 6

typedef struct {
    int i,j;
    int e;
}Tuple;

typedef struct {
    Tuple data[MAXSIZE];
    int mu,nu,tu;
    int DataNum;
}TSMatrix;

void CreateTS(TSMatrix *TS){    //创建三元组
    TS->DataNum = 1;
    TS->mu = ARRSIZE;
    TS->nu = ARRSIZE;
    TS->tu = 0;
}

void transferTS(int array[ARRSIZE][ARRSIZE], TSMatrix *ts){ //矩阵转成三元组
    for(int i = 0;i<ARRSIZE;i++) {
        for (int j = 0; j < ARRSIZE; j++) {
            if(array[i][j] != 0){
                ts->data[ts->DataNum].i = i + 1;
                ts->data[ts->DataNum].j = j + 1;
                ts->data[ts->DataNum].e = array[i][j];
                ts->DataNum++;
                ts->tu++;
            }
        }
    }
}

void PrintTS(TSMatrix *ts){     //打印三元组矩阵
    for (int i = 1; i < ts->DataNum; ++i) {
        printf("%d %d %d\n",ts->data[i].i,ts->data[i].j,ts->data[i].e);
    }
}

void FastTranSMatrix(TSMatrix *M,TSMatrix *T){  //快速转置,M is origin
    T->tu = M->tu;
    T->DataNum = M->DataNum;
    int num[ARRSIZE+1];
    int cpot[ARRSIZE+1];
    int col;
    int q;
    if(T->tu){
        for (col = 1;col<=M->nu;col++)
            num[col] = 0;
        for (int i = 1;i<=M->tu;i++)
            num[M->data[i].j]++;
        cpot[1] = 1;
        for(col = 2;col<=M->nu;col++)
            cpot[col] = cpot[col - 1] + num[col - 1];
        for(int p = 1;p<=M->tu;p++){
            col = M->data[p].j;
            q = cpot[col];
            T->data[q].i = M->data[p].j;
            T->data[q].j = M->data[p].i;
            T->data[q].e = M->data[p].e;
            cpot[col]++;
        }
    }
}

void tranferArrPrint(TSMatrix *ts){         //将三元组转换成矩阵，然后直接输出
    int arr[ARRSIZE][ARRSIZE];
    for(int i = 0;i<ARRSIZE;i++)
        for (int j = 0; j < ARRSIZE; ++j) {
            arr[i][j] = 0;
        }
    for(int i = 1; i<ts->DataNum;i++){
        arr[ts->data[i].i-1][ts->data[i].j-1] = ts->data[i].e;
    }
    for(int i = 0;i<ARRSIZE;i++) {
        for (int j = 0; j < ARRSIZE; ++j) {
            printf("%d ", arr[i][j]);
        }
        printf("\n");
    }
}

int main(){
    TSMatrix TS;
    TSMatrix SM;
    int a[ARRSIZE][ARRSIZE] = {0};
    CreateTS(&TS);
    CreateTS(&SM);

    for(int i = 0;i<ARRSIZE;i++) {
        for (int j = 0; j < ARRSIZE; j++) {
            scanf("%d", &a[i][j]);
        }
    }

    transferTS(a,&TS);
    FastTranSMatrix(&TS, &SM);
    PrintTS(&TS);
    printf("\n");
    PrintTS(&SM);
    printf("\n");
    tranferArrPrint(&SM);
}

---

3.广义表（个人理解）：

        因为课程未要求代码实现等内容，故阐述几个概念，以做复习只用。

        深度：括弧重数，例如：()深度是1、(())深度是2；

        长度：在深度为1的时候，逗号所隔开的子表数，例如：( , , , )长度是4；

        表头：第一个元素，例如：(b,k,p,h)为b，((a,b),(c,d))为(a,b)；

        表尾：除第一个元素之外的元素（但是要注意表示方法），例如：(b,k,p,h)为(k,p,h)，((a,b),(c,d))为((c,d))。

---

4.后记：

        这里似乎除了那个算法，好多都是一笔带过，没有多提，PTA上的课后习题也只是对于三元组和矩阵转置的应用，因此应当对其他内容的代码要求不大，但是有一些概念还是很重要的。

---

return 0;                 //朔风如解意