LSTM结构理解与python实现
上篇博客中提到,简单的RNN结构求解过程中易发生梯度消失或梯度爆炸问题,从而使得较长时间的序列依赖问题无法得到解决,其中一种越来越广泛使用的解决方法就是 Long Short Term Memory network (LSTM)。本文对LSTM做一个简单的介绍,并用python实现单隐藏层LSTM。
参考资料:
- 理解LSTM: http://colah.github.io/posts/2015-08-Understanding-LSTMs/ (一个非常棒的博客,对LSTM基本结构的讲解浅显易懂)
- LSTM前向和后向传播:http://arunmallya.github.io/writeups/nn/lstm/index.html#/ (公式简单明了)
- Alex Graves的博士论文:Supervised Sequence Labelling with Recurrent Neural Networks (详细的公式推导)
1. 理解 LSTM
(1) 前向计算
LSTM是一类可以处理长期依赖问题的特殊的RNN,由Hochreiter 和 Schmidhuber于1977年提出,目前已有多种改进,且广泛用于各种各样的问题中。LSTM主要用来处理长期依赖问题,与传统RNN相比,长时间的信息记忆能力是与生俱来的。
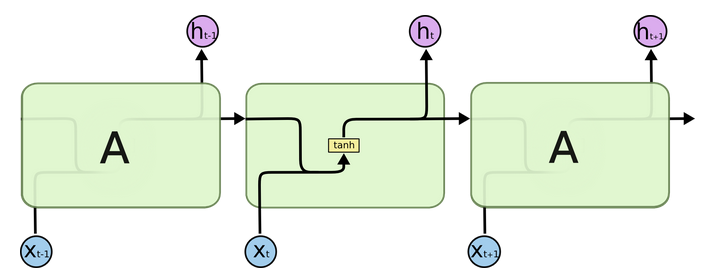
所有的RNN链式结构中都有不断重复的模块,用来随时间传递信息。传统的RNN使用十分简单的结构,比如 tanh 层 (如下图所示)。
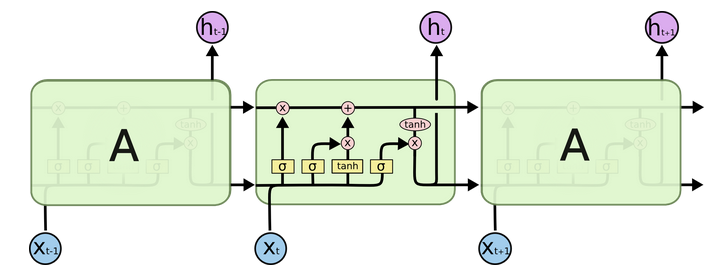
LSTM链式结构中重复模块的结构更加复杂,有四个互相交互的层 (如下图所示)。
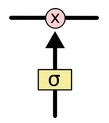
图中各种符号含义如下图所示,黄色的方框表示神经网络层,圆圈表示两个向量间逐点操作,直线箭头表示向量流向,汇聚箭头表示向量串接,分裂箭头表示向量复制流向不同的方向。

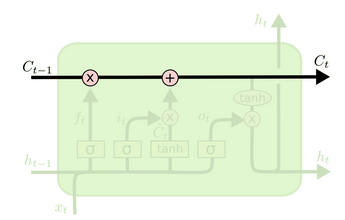
与传统RNN相比,除了拥有隐藏状态外,LSTM还增加了一个细胞状态(cell state,即下图中最上边的水平线),记录随时间传递的信息。在传递过程中,通过当前输入、上一时刻隐藏层状态、上一时刻细胞状态以及门结构来增加或删除细胞状态中的信息。门结构用来控制增加或删除信息的程度,一般由 sigmoid 函数(值域 (0,1) )和向量点乘来实现。
LSTM共包含3个门结构,来控制细胞状态和隐藏状态,下边分别进行介绍。
遗忘门 (output gate)
从名字易知,遗忘门决定上一时刻细胞状态 Ct−1 中的多少信息(由 ft 控制,值域为 (0,1) ) 可以传递到当前时刻 Ct 中。
输入门 (input gate)
顾名思义,输入门用来控制当前输入新生成的信息 C¯t 中有多少信息(由 it 控制,值域为 (0,1) )可以加入到细胞状态 Ct 中。 tanh 层用来产生当前时刻新的信息, sigmoid 层用来控制有多少新信息可以传递给细胞状态。
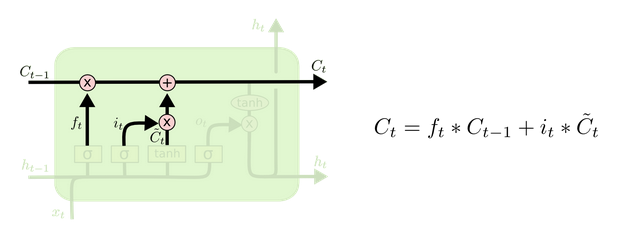
更新细胞状态
基于遗忘门和输入门的输出,来更新细胞状态。更新后的细胞状态有两部分构成,一,来自上一时刻旧的细胞状态信息 Ct−1 ;二,当前输入新生成的信息 C¯t 。前面提到,旧信息有遗忘门 ( ft ) 控制,值为遗忘门的输出点乘旧细胞状态 ( ft∗Ct−1 );新信息由输入门 ( it ) 控制,值为输入门的输出点乘新信息 it∗C¯t 。
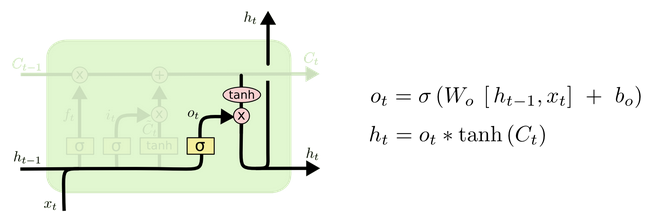
输出门 (output gate)
最后,基于更新的细胞状态,输出隐藏状态 ht 。这里依然用 sigmoid 层 (输出门, ot ) 来控制有多少细胞状态信息 ( tanh(Ct) ,将细胞状态缩放至 (−1,1) ) 可以作为隐藏状态的输出 ht 。
以上是LSTM的前向计算过程,下面介绍求解梯度的反向传播算法。
(2) 梯度求解:BPTT 随时间反向传播
(1) 前向计算各时刻遗忘门状态 ft 、输入门状态 it 、当前输入新信息 C¯t 、细胞状态 Ct 、输出门状态 ot 、隐藏层状态 ht 、模型输出 yt ;
(2) 反向传播计算误差 δ ,即模型目标函数 E 对加权输入
(3) 求解模型目标函数
δ 沿时间 t 的反向传播
定义
由于 ht=ot∗tan








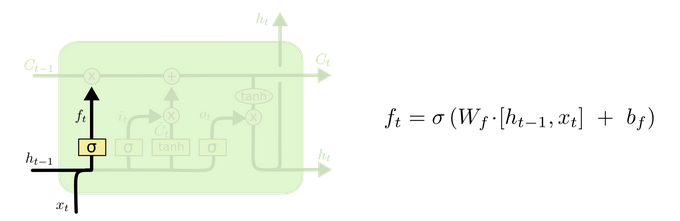
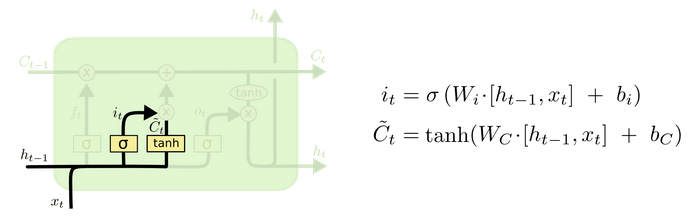
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 2万+
2万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








