可持久化线段树

可持久化线段树，俗称主席树
我其实也不是很懂就来瞎口胡一通看看能不能自己卡死自己而已。。

所谓可持久化，即支持询问之前的状态
比如经过了k次操作后，我们仍然能知道第i次（1<=i<=k） 次操作后的线段树是什么样子的
”然而这只是主席树很小的一部分作用“——szb
蒟蒻瑟瑟发抖
那这要怎么做到呢？k次操作难道建k棵线段树么？显然空间爆炸啊
浪费的信息越少，一个算法越优
我们可以发现，线段树的一次更新，只会对一条链上的信息改变，所以对于除了这一条链上的信息以外，我们可以继承之前的树
比如这样
第一棵树：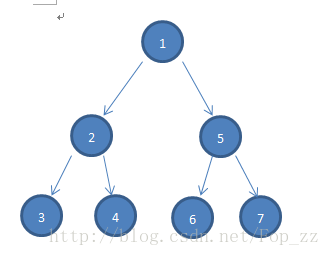
操作一次后

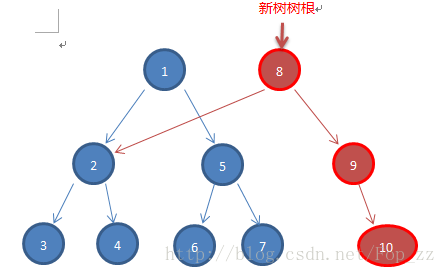
这样从8开始访问，得到的就是一次操作后的树，从1开始，则是初始的树

那么这样做的用处在于什么呢
poj2104
题意大概就是，求l-r之间的k小值

这题很多做法。。这里就只是说一下主席树的做法

我们记录一个数x在整个数列中的排名a[i]
然后建树
一个节点的权值为当前状态（放入前1~i个数）下，在这个节点的l~r区间（排名）内的数有多少个

inline void build(int l,int r,int &x)
{
    x=++tot;
    val[x]=0;
    if(l==r)    return;
    int mid=(l+r)>>1;
    build(l,mid,L[x]);
    build(mid+1,r,R[x]);
}
inline void update(int aci,int &x,int l,int r,int v)
{
    x=++tot;
    val[x]=val[aci]+1;
    L[x]=L[aci];
    R[x]=R[aci];
    if(l==r)    return;
    int mid=(l+r)>>1;
    if(v<=mid)  update(L[aci],L[x],l,mid,v);else update(R[aci],R[x],mid+1,r,v);
}

然后根据观察可以发现，其实build是不需要的。。
因为update后，有用的节点自然会被开出来

分析一下update的代码实现
首先我们把一个新的节点的左右子树全部继承前一棵子树中，与他等价的节点的左右子树。然后找到要更新的那个节点（二选一），把之前的继承覆盖掉即可。
这样我们就只要更新一条链就能构造出一棵新的线段树

然后查询怎么办？
。。这个我只能说，针对此题
比如我们要查询的区间为[X,Y]
然后我们枚举到一个节点p
那么X~Y之间，在p.l~p.r之间的数字数量就是：p(X-1次操作时).v-p(Y次操作时).v
如果这个值大于k，则说明我们要查询的第k小值，在p这个节点中找不到。。

inline int query(int x,int y,int l,int r,int v)
{
    if(l==r)    return l;
    int now=val[L[y]]-val[L[x]];
    int mid=(l+r)>>1;
    if(now>=v)  return query(L[x],L[y],l,mid,v);else return query(R[x],R[y],mid+1,r,v-now);
}

就是说当左区间不足以得到k小值的时候，在右区间找到第k-左区间拥有的数

代码：

#include<bits/stdc++.h>
#define For(i,j,k) for(int i=j;i<=k;i++)
using namespace std;
int L[2000001],R[2000001],val[2000001],root[100001],a[100001],t[100001];
int n,m,tot,len;
inline void update(int aci,int &x,int l,int r,int v){
    x=++tot;
    val[x]=val[aci]+1;
    L[x]=L[aci];
    R[x]=R[aci];
    if(l==r)    return;
    int mid=(l+r)>>1;
    if(v<=mid)  update(L[aci],L[x],l,mid,v);else update(R[aci],R[x],mid+1,r,v);
}
inline int query(int x,int y,int l,int r,int v){
    if(l==r)    return l;
    int now=val[L[y]]-val[L[x]];
    int mid=(l+r)>>1;
    if(now>=v)  return query(L[x],L[y],l,mid,v);else return query(R[x],R[y],mid+1,r,v-now);
}
int main(){
    scanf("%d%d",&n,&m);
    For(i,1,n)  scanf("%d",&a[i]);
    For(i,1,n)  t[i]=a[i];
    sort(t+1,t+n+1);
    len=unique(t+1,t+n+1)-t-1;
    For(i,1,n)  a[i]=lower_bound(t+1,t+len+1,a[i])-t,update(root[i-1],root[i],1,len,a[i]);
    For(i,1,m){
        int t1,t2,k;
        scanf("%d%d%d",&t1,&t2,&k);
        printf("%d\n",t[query(root[t1-1],root[t2],1,len,k)]);
    }
}