SAGAN

最新推荐文章于 2024-06-22 09:36:30 发布

Forlogen

最新推荐文章于 2024-06-22 09:36:30 发布

阅读量3.2k

点赞数 5

分类专栏： GAN

本文链接：https://blog.csdn.net/Forlogen/article/details/90814274

版权

GAN 专栏收录该内容

46 篇文章

订阅专栏

《Self-Attention Generative Adversarial Networks》

github

从本文的题目中可以看出，作者将Attention model中的Self-Attention和生成对抗网络（Generative Adversarial Networks,GAN）结合到了一起，这样做解决了GAN中的什么问题呢，或是使用注意力机制有什么优势呢？下面我们就来看一下文章的主要内容。

虽然GAN经过不断的发展，在图像生成等领域已经取得了很不错的效果，各式各样的变体也是非常的多。即使不同的GAN所解决的任务不完全相同，生成图像的效果也有一定的差异，但是绝大数的模型都是基于卷积神经网络（Convolutional Neural Network，CNN）的架构。由于CNN中局部感受野机制的存在，它只能从提取到的低分辨率特征中提取相关的信息，缺乏对高分辨率特征的理解和各类特征的长期记忆。而且在目前使用的很多模型中，我们常用的往往都是比较小的卷积核，例如 $\times 1$ 或是 $\times 3$ ，使得这样的问题难以解决。

为了捕获更多的图像，更好的提取关于输入的特征，单纯的增加感受野的大小可行吗？原理上它应该可以达到目的，但是它会降低较小的卷积核的计算效率，而且会使得卷积操作变慢。另一方面，我们使用较小的卷积核，但是网络的深度很深，能否达到想要的效果？理论上同样是可行的，但是越深的网络模型通常会导致更多的参数，从而为之后的训练增加了难度。那么如何双管齐下，既可以保证计算的效率，又可以拥有更大的感受野呢，一个极好的解决方案便是自注意力（self-Attention）机制。

如何理解注意力机制，可参阅下面的这篇博文

张俊林博士《深度学习中的注意力机制》

因此作者针对于图像生成任务提出了一个由注意力驱动、具有长程依赖性的GAN的变体，相比于传统的基于卷积网络的模型，它可以从低分辨率图像中所有位置的细节线索来生成高分辨率细节特征，而且判别器可以检查图像的远端部分中的高度详细的特征是否彼此一致，同时为了提升生成器的效果，作者这里还引入了谱归一化（spectral normalization）。

SAGAN通过利用图像远端部分的互补特征而不是局部固定形状的区域来生成图像，从而生成一致的对象/场景，如何理解呢？下面我们先通过文中给出的实例直观上看一下，熟悉注意力机制的同学应该不难看懂它做了什么。在下图的在每一行中，第一个图像显示了5个我们想要查询的具有代表性位置，分别用5个彩色的点进行标记。同一行中的另外五幅图像是这些查询位置的注意力图，用相应的彩色编码箭头概括了最受关注的区域。从中我们可以看出，在GAN中引入注意力机制后，当生成图像中的每一个点时，我们可以考虑全局中与它可能相关的点，而不只是局限于附近固定形状的点。

那SAGAN具体是如何将Self-Attention和GAN结合起来的呢？下面我们通过文中提供的示意图来看一下，如下所示

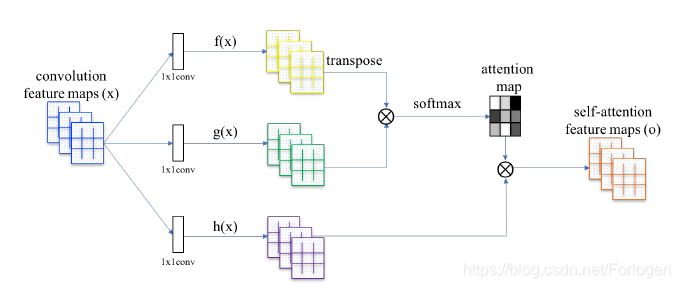
首先同样是通过卷积网络的隐藏层得到卷积的特征图（convolution feature maps） $x$ ，然后通过 $\times 1$ 的卷积核得到两个特征空间（feature space） $f=W_{f}x$ 和 $g=W_{g}x$ ，然后使用 $f$ 和 $g$ 来计算注意力，公式如下所示 $\beta_{j, i}=\frac{\exp \left(s_{i j}\right)}{\sum_{i=1}^{N} \exp \left(s_{i j}\right)}, \text { where } s_{i j}=f\left(x_{i}\right)^{T} g\left(x_{j}\right)$
其中 $\beta_{j,i}$ 表示在生成第 $j$ 个位置时对于第 $i$ 个局部的注意力，然后将结果经过softmax归一化得到注意力图（attention map）。接着使用得到的注意力图和通过另一个 $\times 1$ 卷积核得到的特征空间计算得到注意力层的输出，如下所示 $o_{j}=\sum_{i=1}^{N} \beta_{j, i} h\left(x_{i}\right), \text { where } h\left(x_{i}\right)=W_{h} x_{i}$

上述的三个权重矩阵 $W_{f}、W_{g}、W_{h}$ 需通过训练学习。最后将注意力层的输出和 $x$ 进行结合，得到最终的输出 $y_{i}=\gamma \boldsymbol{o}_{\boldsymbol{i}}+\boldsymbol{x}_{\boldsymbol{i}}$ ，其中 $\gamma$ 初始设置为0，使得模型可以从简单的局部特征学起，逐渐学习到全局。

最终需要优化的损失函数为 $\begin{array}{l}{L_{D}=-\mathbb{E}_{(x, y) \sim p_{d a t a}}[\min (0,-1+D(x, y))]-\mathbb{E}_{z \sim p_{z}, y \sim p_{d a t a}}[\min (0,-1-D(G(z), y))]} \\ {L_{G}=-\mathbb{E}_{z \sim p_{z}, y \sim p_{d a t a}} D(G(z), y)}\end{array}$

此外作者为了稳定模型的训练，使用了如下的两个技巧：

Spectral normalization：有效地降低了训练的计算量，使得训练更加稳定
two-timescale update rule(TTUR)：训练过程中，给予G和D不同的学习速率，以平衡两者的训练速度

从后续的实验中我们可以看出它们确实很好的稳定了模型的训练，随着迭代次数的增加，FID值在平稳的下降，而Inception score值在逐步的增加

而且在生成器和判别器中使用注意力机制后，我们可以在较前的几层中就可以得到比之前的模型好的效果

最后从生成的结果中可以看出，在保证生成图像逼真度的前提下，对于图像中的细节部分也刻画的相对比较好

参考

https://www.sohu.com/a/238960575_100177858

https://www.jqr.com/article/000240

https://blog.csdn.net/HaoTheAnswer/article/details/82733234

https://yq.aliyun.com/articles/572992