从0开始的数据分析-SPASS篇基础篇

Fracures

于 2025-03-09 21:04:02 发布

阅读量1.5k

点赞数 18

分类专栏：从0开始的数据分析文章标签：数据分析数据挖掘

本文链接：https://blog.csdn.net/Fracures/article/details/146134711

版权

从0开始的数据分析专栏收录该内容

3 篇文章

订阅专栏

SPASS的简单基础操作

参考视频
两小时速通SPASS：社科数据分析
面试的岗位需要SPASS软件，所以抽空看了一下，我对于这个软件的理解就是丰富的ui版本的SQL，降低了一些门槛，更考究的是数据的分析策略，指标等。
视频中主要提及了

描述统计
独立样本t检验
单因素独立样本方差分析
卡方独立性检验
相关分析
线性回归
简单调节效应
简单中介效应
我从这几个出发来谈一些我的理解

一、描述统计

这里主要涉及的有分类变量跟连续变量
分类变量

定义：表示类别或组别的变量，取值是离散的、有限的。

类型：

名义变量（Nominal）：无顺序的类别（如性别：男/女；城市：北京/上海）。

有序变量（Ordinal）：有顺序但无明确数值意义的类别（如教育水平：小学/中学/大学）。

示例：学校（0 vs 1）、性别（男/女）、产品类型（A/B/C）。

连续变量

定义：表示数值型数据，取值是无限的、可测量的，通常具有实际意义的大小关系。

类型：

区间变量（Interval）：数值有顺序和固定间隔，但无绝对零点（如温度：30℃ vs 20℃）。

比例变量（Ratio）：有绝对零点的数值（如身高、体重、成绩）

二、独立样本t检验两两（分类–连续）

利用来自两个总体的样本，推测两个总体的均值是否存在差异,也就是比较不同组样本之间的关系。
在视频中使用了谈恋爱跟成绩之间的关系

进行独立样本t检验前，需满足以下假设：

独立性：两组数据来自独立的样本，无重叠或配对。
正态性：每组数据近似服从正态分布（可通过Shapiro-Wilk检验或直方图验证）。
方差齐性：两组的方差相等（通过莱文方差等同性检验判断）。

独立样本检验中的sig（双尾）也就是我们数学一里面概率经常做到的显著性水平p，当分析出来
p值 < 显著性水平（α，通常为0.05）：拒绝原假设，认为两组均值差异具有统计学意义。
p值 ≥ α：不拒绝原假设，认为差异可能由随机误差导致，无统计学意义。

双尾 vs 单尾检验
双尾检验：关注“是否有差异”（无论方向），适用于无明确方向预期的研究。
（如：比较男女身高是否有差异）
单尾检验：关注“差异方向”（如A组是否显著大于B组），需在分析前明确方向假设。
（如：验证新药效果是否显著优于旧药）

在独立样本t检验中，莱文方差等同性检验（Levene’s Test for Equality of Variances）和平均值等同性t检验（即独立样本t检验）是两个关键步骤。它们的显著性水平（如莱文检验的 p值和 t检验的双尾sig）在分析中具有明确的逻辑关系。
你可以注意到视频给出的统计表格是
在这里插入图片描述
在图中先进行了莱文检验
目的：检验两组独立样本的方差是否相等（即方差齐性假设是否成立）。
原假设（H₀）：两总体方差相等（σ₁² = σ₂²）。
显著性水平（p值）解读：
p < α（如0.05） → 拒绝H₀，认为方差不等（方差不齐）。
p ≥ α → 不拒绝H₀，认为方差相等（方差齐）。
也就是这里的第二列显著性水平分析两组的方差是否有差异，当这里的方差小于0.05时，认为这两个方差不等，用不假设方差相等的校正t检验（如Welch’s t-test）也就是看独立样本t检验每组的第二行。
莱文检验解决的是方差齐性问题，而t检验解决的是均值差异问题。
常见误区
❌ 忽略莱文检验直接看t检验：
可能导致错误选择方差齐性或非齐性的t检验结果，增加统计误判风险。
❌ 仅依赖p值判断实际意义：
即使均值差异显著（双尾sig < 0.05），也需结合效应量（如Cohen’s d）判断差异的实际重要性。
❌ 混淆单尾与双尾检验：
双尾sig默认探索无方向差异，若研究有明确方向假设（如A组 > B组），需提前说明使用单尾检验。
总结
莱文方差等同性检验的显著性水平（p值）决定了后续t检验方法的选择：

若方差齐性成立（p ≥ α）→ 使用标准t检验（假设方差相等）。
若方差不齐（p < α）→ 使用校正t检验（如Welch方法）。

双尾 vs 单尾检验
双尾检验：关注“是否有差异”（无论方向），适用于无明确方向预期的研究。
（如：比较男女身高是否有差异）
单尾检验：关注“差异方向”（如A组是否显著大于B组），需在分析前明确方向假设。
（如：验证新药效果是否显著优于旧药）

效应量
显著性（p值）说明的是“有没有”问题
效应量说明的是“有多大”的问题
显著性（p值）与样本量有关，效应量与样本量无关
核心作用：
补充p值，避免仅依赖统计显著性（如大样本可能得到显著但微小的差异）。
允许跨研究比较结果（如Meta分析中合并不同研究的效应）。
帮助确定研究所需的样本量（功效分析）。
解释标准（Cohen准则）

效应量	d值	实际意义示例
小效应	0.2	差异存在，但实际影响微弱（如成绩提高2分）
中等效应	0.5	差异明显（如成绩提高5分）
大效应	0.8	差异巨大（如成绩提高10分）

效应量的具体计算方式自行查阅

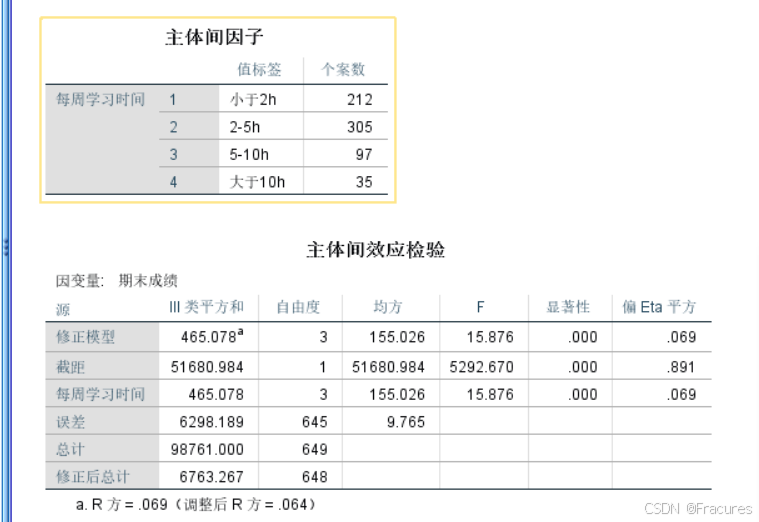
三、样本方差分析多组（分类–连续）

F分布
多项先进行方差分析，判断是否存在方差较大差异；

事后比较
具体各组之间的两两比较
方差齐性：Scheffe（雪费）、Tukey（图基）
方差不齐：Games-Howell（盖姆斯—豪厄尔）
用于细化存在方差差异的组间差异是什么。

效应量同上
在这里插入图片描述

四、卡方独立性检验（分类–分类）

用于判断两个分类变量是否独立

学校户籍关系
![在这里插入图片描述](https://i-blog.csdnimg.cn/direct/9a264c63e890477d92a9e4b2a3f148b0.png
1.独立性：个案之间彼此独立
2.互斥且完整:任意被试一定且只能归属与其中一类
3.期望值大小：
单元格期望值大于等于5，如果存在20%单元格的期望值小于5，则需要Fisher校正
克莱姆V是卡方检验的效应量，用于衡量两个分类变量之间的关联强度，范围在 0到1 之间。
作用：
补充卡方检验，避免仅依赖p值（大样本可能p值显著但实际关联微弱）。
标准化指标，便于跨研究比较关联程度。

克莱姆V值	关联强度	实际意义
0.0	无关联	变量完全独立
0.1	弱关联	关联存在但实际影响微弱
0.3	中等关联	关联明显（需结合领域背景）
0.5+	强关联	变量间高度相关