SPASS-回归分析

回归分析概述

确定性关系与非确定性关系

        变量与变量之间的关系分为确定性关系和非确定性关系，函数表达确定性关系。研究变量间的非确定性关系，构造变量间经验公式的数理统计方法称为回归分析。

回归分析基本概念

        回归分析是指通过提供变量之间的数学表达式来定量描述变量间相关关系的数学过程，这一数学表达式通常称为经验公式。我们不仅可以利用概率统计知识，对这个经验公式的有效性进行判定，同时还可以利用这个经验公式，根据自变量的取值预测因变量的取值。如果是多个因素作为自变量的时候，还可以通过因素分析，找出哪些自变量对因变量的影响是显著的，哪些是不显著的。

回归分析的一般步骤

第1步 确定回归方程中的因变量和自变量。

第2步 确定回归模型。

第3步 建立回归方程。

第4步 对回归方程进行各种检验。

         拟合优度检验

        回归方程的显著性检验

        回归系数的显著性检验

第5步 利用回归方程进行预测。

线性回归分析

基本概念

         线性回归假设因变量与自变量之间为线性关系，用一定的线性回归模型来拟合因变量和自变量的数据，并通过确定模型参数来得到回归方程。根据自变量的多少，线性回归可有不同的划分。当自变量只有一个时，称为一元线性回归，当自变量有多个时，称为多元线性回归。

统计原理

一元回归方程和多元回归方程

一元线性和多元线性回归分析的核心任务就是估计其中的参数。

一元线性回归

第1步 分析：这是一个因变量和一个自变量之间的问题，故应该考虑用一元线性回归解决。

第2步 数据组织：定义三个变量，分别为“year”（年份）、“x”（国内生产总值）、“y”（财政收入）。

第3步 作散点图，观察两个变量的相关性：依次选择菜单“图形→旧对话框→散点/点状→简单分布”，并将“国内生产总值”作为x轴，“财政收入”作为y轴，得到如下所示图形。 

可以看出两变量具有较强的线性关系，可以用一元线性回归来拟合两变量。

主要结果及分析：

        表中显示回归模型编号、进入模型的变量、移出模型的变量和变量的筛选方法。可以看出，进入模型的自变量为“国内生产总值” 。 

        R=0.989，说明自变量与因变量之间的相关性很强。R方(R2) =0.979，说明自变量“国内生产总值”可以解释因变量“财政收入”的97.9%的差异性。

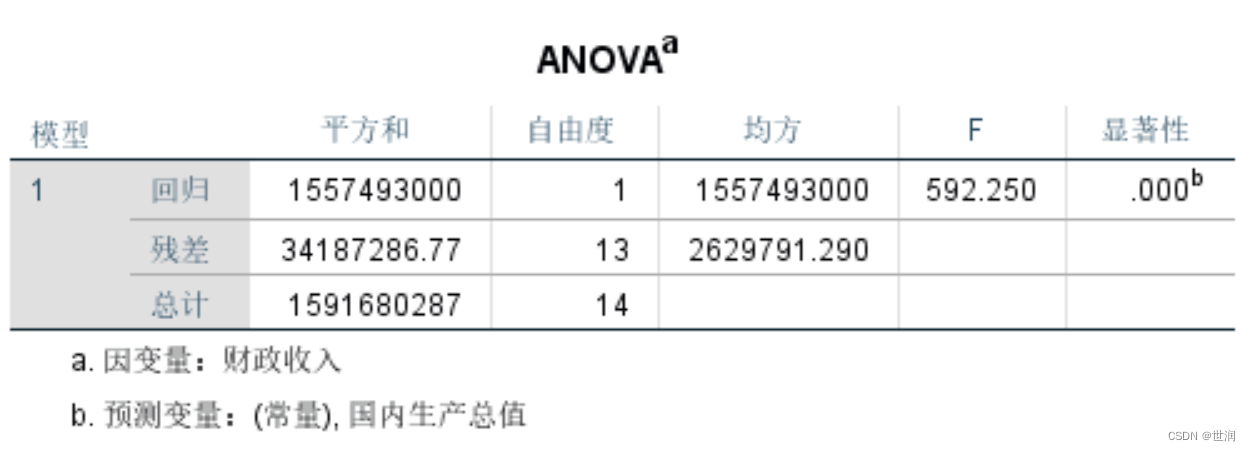
        表中显示因变量的方差来源、方差平方和、自由度、均方、F检验统计量的观测值和显著性水平。方差来源有回归、残差。从表中可以看出，F统计量的观测值为592.25，显著性概率为0.000，即检验假设“H0：回归系数B = 0”成立的概率为0.000，从而应拒绝原假设，说明因变量和自变量的线性关系是非常显著的，可建立线性模型。

        表中显示回归模型的常数项、非标准化的回归系数B值及其标准误差、标准化的回归系数值、统计量t值以及显著性水平（Sig.）。从表中可看出，回归模型的常数项为-4993.281，自变量“国内生产总值”的回归系数为0.197。因此，可以得出回归方程：财政收入=-4993.281 + 0.197 × 国内生产总值。

        回归系数的显著性水平为0.000，明显小于0.05，故应拒绝T检验的原假设，这也说明了回归系数的显著性，说明建立线性模型是恰当的。