使用Macondo软件仿真设计阵列波导光栅（AWG）

使用Macondo软件仿真设计阵列波导光栅（AWG）

   随着信息技术的飞速发展，光通信网络在高速数据传输中的作用日益重要。为了利用现有光通信网络的宽带资源，发展波分复用(Wavelength Division Multiplexing, WDM)，尤其是密集波分复用(Dense Wavelength Division Multiplexing, DWDM)技术，对于光通信网络的升级和超高速通信的支持具有重要意义。在WDM和DWDM系统中，AWG(Arrayed Waveguide Grating)是最具代表性的复用/解复用器件，其性能直接决定了系统的传输质量${}^{[1]}$。本文主要讲解了AWG的原理和参数设计，并在Macondo软件中对AWG的输入部分进行设计和仿真。

一、AWG设计原理

图 1：AWG结构图

   AWG是基于干涉原理的波分复用/解复用器件，它是由输入/输出波导阵列(transmitter waveguide)、自由传输区(FPR)、平板波导(plane waveguide)和弯曲阵列波导(curved array waveguide)5个部分组成，如图1所示。自由空间耦合区具有傅里叶转换透镜的作用，通过阵列波导光栅区引入相位差，实现不同波长信号的复用与解复用。信号从输入波导其中的一个输入，在输入平板波导区模式场发散，由阵列波导的输入孔阑捕捉。阵列波导相邻波导间的长度差 $\Delta L$ 为一常数，不同波长的输入信号引入不同的相位差。随后，光场在输出平板波导区衍射汇聚，不同波长的信号聚焦在像平面的不同位置，通过合理的设计输出波导端口的位置实现信号的输出。

   相邻两弯曲阵列波导具有恒定的长度差$\Delta L$，起衍射光栅的作用，相邻波导的长度满足解耦合条件。阵列波导光栅应该满足光栅方程：

$$n_{s}d\sin {\theta }_i+n_{s}d\sin {\theta }_o+n_c\Delta L=m{\lambda }_0\text{\hspace{1em}(1)}$$
式中，${\theta }_i、{\theta }_o$ 分别为阵列波导对中心输入/输出波导的夹角；$n_s、n_c$ 分别为平板波导、阵列波导的有效折射率；$d$ 为阵列波导的间距；$m$ 为衍射级数；$\lambda$ 为入射波长；$\Delta L$ 为相邻两个阵列波导的长度差。对于中心输入、输出的波导，应该满足下列关系：

$$n_c\Delta L=m{\lambda }_0\text{\hspace{1em}(2)}$$
   可以看出，当衍射角为零时仍可得到高的衍射级数，这一点不同于普通的平面衍射光栅。在光栅中高的衍射级数可提高光栅的分辨率。

   当阵列波导相对于中心输出波导的夹角${\theta }_o$很小时，$\sin {\theta }_o\approx {\theta }_o$，由式(1)可得出 AWG 的角色散关系，即衍射角同波长的关系为：

$$\frac{d\theta }{d\lambda }=\frac{m}{n_{s}d}\cdot \frac{n_g}{n_c}\text{\hspace{1em}(3)}$$
式中，$n_g=n_c-{\lambda }_0\cdot \frac{d{n}_c}{d\lambda }$ 为群折射率。

   在普通的平面衍射光栅中，角色散关系为：

$$\frac{d\theta }{d\lambda }=\frac{m}{n_{s}d}\cdot \frac{1}{\cos \theta }\text{\hspace{1em}(4)}$$

   将式(3)同式(4)进行比较可以看出，在高衍射级数情况下，AWG 中不同波长的衍射影响光峰更易分开。事实上，AWG 是通过阵列波导将平面衍射光栅的相位差增大的改进型光栅，从而命名为阵列波导光栅，其核心在于引入了0角度下的相位差，其发明人 Mr. Smit 将这种器件称为相位器(phaser)。

在设计器件时，可以根据 AWG 的角色散关系来确定通道间隔 $\Delta \lambda$：

$$\Delta \lambda =\Delta \theta \cdot {\left(\frac{d\theta }{d\lambda }\right)}^{-1}=\frac{\Delta x_0}{R}\cdot \frac{n_{s}d}{m}\cdot \frac{n_c}{n_g}\text{\hspace{1em}(5)}$$
   可以看出， $\Delta \lambda$ 反比于 $R\cdot m$ 的乘积，与输出波导间距$\Delta x_o$、阵列波导间距 $d$ 成正比。

二、AWG基本参数

   通过设计AWG的物理参数：衍射级数$m$、罗兰圆聚焦长度$R$、相邻阵列波导的长度差$\Delta L$、波导的折射率差$\Delta n$、单模波导宽度$w$和高度$h$、平板波导和阵列波导的有效折射率$n_s$和$n_c$、输入/输出波导的解耦合距离$\Delta x_i$和$\Delta x_o$、阵列波导的间距$d$、阵列波导数$2j+1$、波导的最小弯曲半径，我们可以得到一个性能良好的AWG。

   设计 AWG 时，先确定基本的参数，包括通道数 $N$，中心波长 ${\lambda }_0$ 或频率 $f_c$，信道间隔 $\Delta \lambda$ 或 $\Delta f_{\text{ch}}$，自由波段区 FSR 等。进一步优化参数时则要考虑插入损耗、通道非均匀性 Lu、串扰 CT (crosstalk)、偏振相关波长 PDW (polarization depended wavelength)、偏振相关损耗 PDL (polarization depended loss)。基本参数的设置规则如下：

1. 波导的宽度 $w$，高度 $h$，平板波导和阵列波导的有效折射率$n_s$ 和 $n_c$。
   

   如果确定了波导包层及芯层材料，在单模条件下，就确定了波导的宽度 w，高度 h，平板波导和阵列波导的有效折射率$n_s$ 和 $n_c$。如果波导的折射率差越小，单模波导尺寸就越大，相应的波导单位长度损耗较小。对于弯曲波导来说，弯曲半径大时的损耗就较小，但会增加器件的整体尺寸。为实现小尺寸紧凑型 AWG，可采用折射率差较大的波导，但小尺寸会增加损耗。
   

2. 输入/输出波导解耦合距离$\Delta x_i$ 和$\Delta x_o$ 和阵列波导的间距$d$
   

   $\Delta x_i$ 和$\Delta x_o$ 是 AWG 的输入和输出波导的解耦合距离，$d$ 是阵列波导的间距，在可能降低相邻波导串扰的前提下，设计出最小$\Delta x_i$ 和$\Delta x_o$ 和 $d$。对称称 AWG 中，这三者相等。串扰 CT 与波导间距离的关系为：
   
   $$C_T=10\cdot \log P_{over}\text{\hspace{1em}(6)}$$
   式中，$P_{over}$ 为串扰功率，表示因波导间耦合、相互干扰或旁路信号等因素，导致的干扰信号的功率，表达式如下：
   
   $$P_{\text{over}}(\Delta x_i,\Delta x_o,d)=\frac{{\left\{0.5\int \left(E_1^{\ast }\times H_2^d+E_2\times H_1^{\ast }\right)dA\right\}}^2}{\int \left(E_1\times H_1^p\right)dA\int \left(E_2\times H_2^{\ast }\right)dA}\text{\hspace{1em}(7)}$$

   $$E_2(x,d)=E_1(x+\Delta x_i,\Delta x_o,d),H_2(x,d)=H_1(x+\Delta x_i,\Delta x_o,d)\text{\hspace{1em}(8)}$$

   式中，波导中场$E_1,H_1,E_2,H_2$ 分别为两相邻波导的电场和磁场强度，可以近似取高斯分布。相关波导间串扰随波导间间距增大呈指数衰减，低折射率差的二氧化硅波导间解耦合的距离为$20\mu m$，SOI 波导中解耦的距离可小到 $1.5\mu m$，大的波导间距可减小串扰，且会使器件的整体尺寸增加，需要在串扰和器件尺寸间进行折中考虑。
   

3. 罗兰圆直径$R$，衍射级数 $m$和阵列波导长度差 $\Delta L$
   

   $R$, $m$ 和 ${\lambda }_0$ 是相互关联的三个量,由通道数$N$、通道间隔 $\Delta \lambda$、中心波长${\lambda }_0$, $n_s$, $n_c$, $\Delta x_o$ 和$d$ 这q七个参数共同决定，在设计时一般先确定 $R$ 或 $m$ 中的一个，然后确定另两个量。由式（5）知，$R$ 和 $m$ 值不是唯一的，只要二者的乘积满足（5）即可。对不同的设计其值 R 和 m 的标准和先后不同。
   

4. 阵列波导数 $N_a (N_a=2j+1) $
   

阵列波导数 $N_a$ 的确定考虑两方面因素：一方面，在阵列波导的输入端能够收集从输入平板波导衍射出的足够能量；另一方面，阵列波导输出端的阵列数目足够大，以致输出谱的旁瓣得到有效抑制，降低串扰。 一般选取阵列波导收集功率为输出率的$1/e$，阵列波导条数满足：

$$N_a\ge \frac{2{\theta }_{\text{max}}R}{d_a}+1=\frac{{\lambda }_0\cdot R}{\pi n_s{\omega }_{0}d}\text{\hspace{1em}(9)}$$
式中，${\theta }_{\text{max}}$ 是阵列波导相对于中心输入波导的最大张角。

上述原则确定了AWG的基本参数后，就可以进行AWG的版图布局${}^{[1]}$。

三、Macondo软件中的布局与仿真

   根据参考文献[3]，模型的基本参数确定如下：

表 1：模型基本参数

   AWG输入部分包含24个阵列波导，两个相切在一起的圆，一个多边形和一个输入波导，在Macondo中用脚本建立几何模型，并添加求解器，在每一个输出波导位置添加监控器，输入波导位置添加光源，得到的模型如图2所示，

图 2：Macondo中AWG输入波导阵列、自由传播区和平板波导结构 完整的AWG模型如图3所示，
 图 3：Macondo中AWG完整结构

   光源从左侧输入，经过自由传播区传播到阵列波导中，在输出端输出时，不同波导的光发生了相位的变化，在输出部分的自由传播区发生干涉，不同波长的光聚焦到不同的波导中，从波导中输出。

   对输入部分进行仿真，得到波长为1.6μm时，波导中的场分布如图4所示，

图 4：输入部分的场分布

   在每一个波导上添加T监控器，将得到的Transmission数据和相应的波长、波导绘图，得到图5所示的结果，

图 5：每个波导中不同波长的光对应的强度    正如预期的那样，在中心波导处获得了最大传输强度，但函数并不平滑。可以通过优化输入耦合器设计来改善这一点。
 图 6：总传输强度    图6给出了通过对所有Narray波导的波长依赖性求和得到的总传输强度，该图反映了阵列波导光栅对不同波长的整体透过率和传输效果。

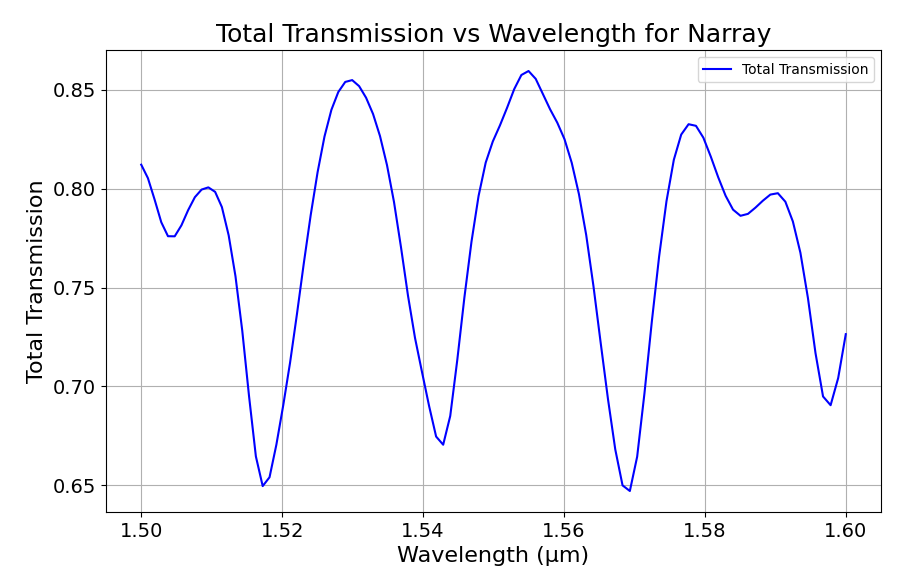
   图5可以直观的观察到各个波导中不同波长的传输强度。图6有助于分析AWG的波长选择性和其在1.5μm~1.6μm波长范围内的性能。

四、总结与展望

   本文通过 Macondo 软件对阵列波导光栅(AWG)进行了建模与仿真，介绍了其工作原理、设计参数及仿真结果。在当前的仿真中，我们主要关注了 AWG 的核心部分和阵列波导的传输特性。接下来，计划将焦点转向 AWG 的输出部分，进一步探讨输出波导与外部设备之间的连接及其对传输效率的影响。之后，我们将提取器件仿真参数，串联链路仿真软件，评估AWG在链路的整体性能。

五、参考文献

[1] 余金中.《硅光子学》.北京：科学出版社，2011.

[2] Meint K. Smit et al., “PHASAR-Based WDM-Devices: Principles, Design and Applications,” IEEE Journal of Selected Topics in Quantum Electronics, 2, 1996.

[3] Hongqiang Li et al., “Investigation of Ultrasmall 1×N AWG for SOI-Based AWG Demodulation Integration Microsystem”, IEEE Photonics Journal, 7, 2015.

[4] A. Abrardo and G. Cincotti, “Design of AWG Devices for All-Optical Time-Frequency Packing,” in Journal of Lightwave Technology, vol. 32, no. 10, pp. 1951-1959, May15, 2014.