K-近邻算法原理介绍以及kd树实现K-近邻算法
K近邻算法是一种常用的有监督的机器学习方法,k-近邻算法也被称为KNN算法,它可以解决分类问题,也可以解决回归问题。本文的主要内容如下:
l KNN算法的原理以及优缺点
l KNN算法的三个基本要素
l KNN算法的基本实现步骤
l kd树以及kd树实现k-近邻算法
1. KNN算法的原理
KNN算法的工作原理非常简单:给定一个训练数据集,对新的输入实例,在训练集中找到与该实例最邻近的K个实例(也就是k个邻居),这k个实例的多数属于某个类,就把该输入实例分类到这个类中。
举例说明:
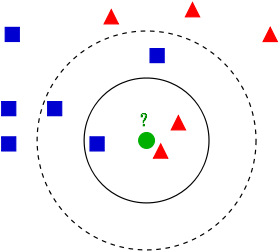
如上图所示,有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所标示的数据则是待分类的数据。
问题:给这个绿色的圆分类?
如果k=3,绿色圆点的最近的3个邻居是2个红色小三角形和1个蓝色小正方形,少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。
如果k=5,绿色圆点的最近的5个邻居是2个红色三角形和3个蓝色的正方形,还是少数从属于多数,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
1.1 KNN算法的优缺点
l 优点:
-
简单,易于理解,无需建模与训练,易于实现;
-
适合对稀有事件进行分类;
-
适合与多分类问题,例如根据基因特征来判断其功能分类,KNN比SVM的表现要好。
l 缺点:
-
惰性算法,内存开销大,对测试样本分类时计算量大,性能较低;
-
可解释性差,无法给出决策树那样的规则。
2.KNN算法的三个基本要素
2.1 k值的选择
k 值的选择会对算法的结果产生重大影响。k值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用,但容易发生过拟合;如果 k 值较大,优点是可以减少学习的估计误差,但缺点是学习的近似误差增大,这时与输入实例较远的训练实例也会对预测起作用,使预测发生错误。具体应用中k值的选择需要通过大量的实验来选择。
2.2 距离度量
K近邻算法的核心在于找k个最近的邻居,为什么要找距离最近的k个邻居,那是因为在特征空间中两个实例点的距离可以反应出两个实例点的相似程度,而K近邻模型的特征空间一般是n维实数向量空间,可以使用欧式距离测量两个实例间的距离,也课使用其它距离公式测量,如曼哈顿距离、切比雪夫距离、闵可夫斯基距离(Minkowski Distance)。
2.2.1 欧式距离
最常见的两点之间或多点之间的距离表示法,又称之为欧几里得度量,它定义于欧几里得空间中,如点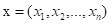 和
和 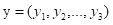 之间的距离为:
之间的距离为:

2.2.2 曼哈顿距离
我们可以定义曼哈顿距离的正式意义为L1-距离或城市区块距离,也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上,坐标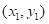 的点P1与坐标
的点P1与坐标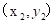 的点P2的曼哈顿距离为:,要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。
的点P2的曼哈顿距离为:,要注意的是,曼哈顿距离依赖座标系统的转度,而非系统在座标轴上的平移或映射。
通俗来讲,想象你在曼哈顿要从一个十字路口开车到另外一个十字路口,驾驶距离是两点间的直线距离吗?显然不是,除非你能穿越大楼。而实际驾驶距离就是这个“曼哈顿距离”,此即曼哈顿距离名称的来源, 同时,曼哈顿距离也称为城市街区距离(City Block distance)。
2.2.3 切比雪夫距离
切比雪夫距离(Chebyshev distance),二个点之间的距离定义为其各坐标数值差的最大值。点P1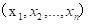 和P2
和P2 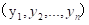 的距离如下:
的距离如下:
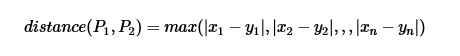
2.2.4 闵可夫斯基距离(Minkowski Distance)
闵尔科夫斯基距离(闵式距离),以俄国科学家闵尔科夫斯基命名,是欧氏距离的推广,是一组距离的的定义。点P1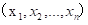 和P2
和P2 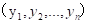 的距离如下:
的距离如下:
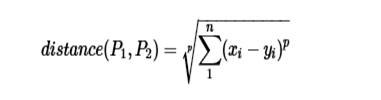
当p=1时,就是曼哈顿距离;
当p=2时,就是欧式距离;
当p→∞时,就是切比雪夫距离;
根据参数的不同,闵氏距离可以表示一类的距离。
2.3 分类决策规则
往往是多数表决,即由输入实例的 K 个最临近的训练实例中的多数类决定输入实例的类别。
3. KNN算法的基本实现步骤
算法基本步骤:
1)计算待分类点与已知类别的点之间的距离
2)按照距离递增次序排序
3)选取与待分类点距离最小的k个点
4)确定前k个点所在类别的出现次数
5)返回前k个点出现次数最高的类别作为待分类点的预测分类
下面是一个按照算法基本步骤用matlab实现的简单例子,根据已分类的9个样本点来预测未知点(如图蓝色x点(1.6,0.3))的分类:

%实现KNN算法
%%算法描述
%1、初始化训练集和类别;
%2、计算测试集样本与训练集样本的欧氏距离;
%3、根据欧氏距离大小对训练集样本进行升序排序;
%4、选取欧式距离最小的前K个训练样本,统计其在各类别中的频率;
%5、返回频率最大的类别,即测试集样本属于该类别。
clear all
clc
%%算法实现
%step1、初始化训练集、测试集、K值
%创建一个三维矩阵,二维表示同一类下的二维坐标点,第三维表示类别
trainData1=[0 0;0.1 0.3;0.2 0.1;0.2 0.2]; %第一类训练集
trainData2=[1 0;1.1 0.3;1.2 0.1;1.2 0.2];%第二类训练集
trainData3=[0 1;0.1 1.3;0.2 1.1;0.2 1.2]; %第三类训练集
trainData(:,:,1)=trainData1;%设置第一类测试数据
trainData(:,:,2)=trainData2;%设置第二类测试数据
trainData(:,:,3)=trainData1;%设置第三类测试数据
trainDim=size(trainData);%获取训练集的维数
testData=[1.6 0.3];%设置1个测试点
k=7;
%%分别计算测试集中各个点与每个训练集中的点的欧氏距离
%把测试点扩展成矩阵
testData_rep=repmat(testData,4,1);
%设置三个二维矩阵存放测试集与测试点的扩展矩阵的差值平方
%diff1=zero(trainDim(1),trianDim(2));
%diff2=zero(trainDim(1),trianDim(2));
%diff3=zero(trainDim(1),trianDim(2));
for i=1:trainDim(3)
diff1=(trainData(:,:,1)-testData_rep).^2;
diff2=(trainData(:,:,2)-testData_rep).^2;
diff3=(trainData(:,:,3)-testData_rep).^2;
end
%设置三个一维数组存放欧式距离
distance1=(diff1(:,1)+diff1(:,2)).^2;
distance2=(diff2(:,1)+diff2(:,2)).^2;
distance3=(diff3(:,1)+diff3(:,2)).^2;
%将三个一维数组合成一个二维矩阵
temp=[distance1 distance2 distance3];
%将这个二维矩阵转换为一维数组
distance=reshape(temp,1,3*4);
%对距离进行排序
distance_sort=sort(distance);
%用一个循环寻找最小的K个距离里面那个类里出现的频率最高,并返回该类
num1=0;%第一类出现的次数
num2=0;%第二类出现的次数
num3=0;%第三类出现的次数
sum=0;%sum1,sum2,sum3的和
for i=1:k
for j=1:4
if distance1(j)==distance_sort(i)
num1=num1+1;
end
if distance2(j)==distance_sort(i)
num2=num2+1;
end
if distance3(j)==distance_sort(i)
num3=num3+1;
end
end
sum=num1+num2+num3;
if sum>=k
break;
end
end
class=[num1 num2 num3];
classname=find(class(1,:)==max(class));
fprintf(‘测试点(%f %f)属于第%d类’,testData(1),testData(2),classname);
%%使用绘图将训练集点和测试集点绘画出来
figure(1);
hold on;
for i=1:4
plot(trainData1(i,1),trainData1(i,2),'*');
plot(trainData2(i,1),trainData2(i,2),'o');
plot(trainData3(i,1),trainData3(i,2),'>');
end
plot(testData(1),testData(2),‘x’);
text(0.1,0.1,‘第一类’);
text(1.1,0.1,‘第二类’);
text(0.1,1,‘第三类’);
结果如下:

4. kd树以及kd树实现k-近邻算法
4.1 kd树
实现k近邻算法时,主要考虑的问题是如何对训练数据进行快速k近邻搜索。这在特征空间的维数大及训练数据容量大时尤其必要。k近邻算法最简单的实现是线性扫描(穷举搜索),即要计算输入实例与每一个训练实例的距离。计算并存储好以后,再查找K近邻。当训练集很大时,计算非常耗时。为了提高kNN搜索的效率,可以考虑使用特殊的结构存储训练数据,以减小计算距离的次数。
kd树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是一种二叉树,表示对k维空间的一个划分,构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分,构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据点的搜索,从而减少搜索的计算量。
4.2 构造kd树
输入:k维空间数据集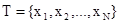 ,其中
,其中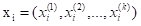 ,
,








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 4532
4532











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








