【数学建模】常用基本模型总结

沐兮Krystal

已于 2022-08-06 19:39:15 修改

阅读量2.2k

点赞数

文章标签： matlab 算法动态规划

于 2022-07-25 16:57:55 首次发布

本文链接：https://blog.csdn.net/GW_Krystal/article/details/125978054

版权

1. 线性规划（Linear Programming)

运筹学的一个重要分支——数学规划。线性规划是在一组线性约束条件的限制下，求一线性目标函数最大或最小的问题。
概念：可行解、最优解、可行域。
Matlab中求解线性规划的命令为如下，x返回决策向量的取值；fval返回目标函数的最优值；f为价值向量。

[x,fval] = linprog(f,A,b,Aeq,beq,lb,ub)

很多看起来不是线性规划的问题，也可以通过变换转化为线性规划的问题来解决。
比如对于以下数学规划问题：
$\begin{array}{c} \min \left|x_{1}\right|+\left|x_{2}\right|+\cdots+\left|x_{n}\right| \\ \text { s.t. } \boldsymbol{A} \boldsymbol{x} \leqslant \boldsymbol{b}_{\circ} \end{array}$
只要注意到事实：
对任意的 $x_i$ ，存在 $u_i,v_i \ge 0$ 满足 $x_{i}=u_{i}-v_{i},\left|x_{i}\right|=u_{i}+v_{i }$
所以取 $u_{i}=\frac{x_{i}+\left|x_{i}\right|}{2}, v_{i}=\frac{\left|x_{i}\right|-x_{i}}{2}$ ，记 $\boldsymbol{u}=\left[u_{1}, \cdots, u_{n}\right]^{\mathrm{T}}, \boldsymbol{v}=\left[v_{1}, \cdots, v_{n}\right]^{\mathrm{T}}$ ，
从而把模型改写成：
$\begin{array}{ll} \min & \sum_{i=1}^{n}\left(u_{i}+v_{i}\right), \\ \text { s.t. } \quad & \left\{\begin{array}{l} {[\boldsymbol{A},-\boldsymbol{A}]\left[\begin{array}{l} \boldsymbol{u} \\ \boldsymbol{v} \end{array}\right] \leqslant \boldsymbol{b},} \\ \boldsymbol{u}, \boldsymbol{v} \geqslant 0 。 \end{array}\right. \end{array}$

投资的收益和风险（多目标规划模型）：

模型一：给定风险一个界限a，把多目标规划变成一个目标的线性规划；
模型二：投资者希望总盈利至少达到水平k以上，固定盈利水平，极小化风险；
模型三：投资者在权衡资产风险和预期收益两方面，希望选择一个令自己满意的投资组合。因此对风险、收益分别赋予权重 $s\le 1)$ 和 $1 - s$ ，称为投资偏好系数。

2. 整数规划

数学规划中的变量（部分或全部）限制为整数时，称为整数规划。
整数线性规划模型大致可分为两类：
（1）变量全限制为整数时，称为纯（完全）整数规划；
（2）变量部分限制为整数时，称为混合整数规划。
求解方法分类：
（1）分枝定界法
（2）割平面法
（3）隐枚举法——求解”0-1“整数规划（包括过滤和分枝）
（4）匈牙利法——解决指派问题
（5）蒙特卡洛法——求解各种类型规划

0-1 型整数规划

变量 $x_j$ 仅取值0或1。
相互排斥的约束条件：如果有 $m$ 个互相排斥的约束条件，为了保证这 $m$ 个约束条件只有一个起作用，引入 $m$ 个 0-1 变量 $y_i$ 和一个充分大的常数M。
关于固定费用的问题（Fixed Cost Problem）
指派问题的数学模型：分配n人去做n项工作，每人做且仅做一项工作。（可用匈牙利算法。拍卖算法等求解）

蒙特卡洛法（随机取样法）

也称为计算机随机模拟方法。使用蒙特卡洛方法必须使用计算机生成相关分布的随机数。
设计随机实验求解图形面积的近似值：在矩形区域产生服从均匀分布的随机点，统计随机点落在曲边三角形的频数。计算的Matlab程序如下：

x = unifrnd(0,12,[1,10000000]);
y = unifrnd(0,9,[1,10000000]);
pinshu = sum(y<x.^2&x<=3)+sum(y<12-x&x>=3);
area_appr=12*9*pinshu/10^7

尽管整数规划由于限制变量为整数而增加了难度；然而由于整数解是有限个，为枚举法提供了方便。
应用概率理论可以证明，在一定计算量的情况下，用蒙特卡洛法可以得出一个满意解。

非线性整数规划

应用蒙特卡洛法去随机计算 $10^6$ 个点便可以找到满意解。
$\begin{array}{ll} \max z=x_{1}^{2}+x_{2}^{2}+3 x_{3}^{2}+4 x_{4}^{2}+2 x_{5}^{2}-8 x_{1}-2 x_{2}-3 x_{3}-x_{4}-2 x_{5}, \\ \text { s.t. }\left\{\begin{array}{l} 0 \leqslant x_{i} \leqslant 99, i=1, \cdots, 5 \\ x_{1}+x_{2}+x_{3}+x_{4}+x_{5} \leqslant 400 \\ x_{1}+2 x_{2}+2 x_{3}+x_{4}+6 x_{5} \leqslant 800 \\ 2 x_{1}+x_{2}+6 x_{3} \leqslant 200 \\ x_{3}+x_{4}+5 x_{5} \leqslant 200 \end{array}\right. \end{array}$
首先编写M文件mente.m定义目标函数f和约束向量函数g，程序如下：

function [f,g]=mengte(x);
f = x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)-3*x(3)-x(4)-2*x(5);
g = [sum(x)-400
    x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800
    2*x(1)+x(2)+6*x(3)-200
    x(3)+x(4)+5*x(5)-200];

编写如下Matlab程序求问题的解。

clc,clear
rand('state',sum(clock)); %初始化随机数发生器
p0=0;
tic %计时开始
for i=1:10^6
       x=randi([0, 99],1,5); %产生一行五列的区间[0.99]上的随机整数
       [f,g]=mengte(x);
       if all(g<=0)
          if p0<f
             x0=x;p0=f; %记录下当前较好的解
          end
       end
   end
x0,p0
toc %计时结束

整数线性规划的计算机求解

整数规划问题的求解使用Lingo比较方便，使用Matlab求解时需把所有的决策变量化为一维决策向量。
Matlab求解混合整数线性规划的命令为：

[x,fval]=intlinprog(f,intcon,A,b,Aeq,beq,lb,ub)

对应于如下数学模型：
$\begin{array}{ll} \min _{x} f^{\top} \boldsymbol{x},\\ \text { s.t. }\left\{\begin{array}{l} x(\text { intcon) 为整数, } \\ A \cdot x \leqslant b, \\ \text { Aeq } \cdot x=\mathrm{beq} \\ \mathrm{lb} \leqslant x \leqslant \mathrm{ub}_{\circ} \end{array}\right. \end{array}$

3. 博弈模型

当存在多个决策者，每个决策者有自己的决策变量和目标函数，并且一个决策者的决策变量以某种形式出现在另一个决策者的目标函数中时，决策者之间的决策行为相互影响。
这种决策主体的决策行为发生直接相互作用的多人决策问题一般称为博弈或对策（Game）。
基本假定时所有决策主体是完全理性的，每个决策主体都希望最优化自己的个人目标。
分为合作博弈和非合作博弈；
根据所有决策者的决策是同时做出的，还是按一定先后顺序做出的，非合作博弈可以分为静态博弈和动态博弈；
根据决策者在决策时掌握的信息的多少，非合作博弈可以是完全信息博弈和不完全信息博弈。

进攻与撤退的抉择

博弈参与者为两方（盟军和德军）
博弈中盟军有3种使用其预备队的决策行动：强化缺口、原地待命、东进；德军有2种决策行动：向西进攻或向东撤退。
博弈双方的目的都是要获得最后的胜利，不妨简单假定目的都是使战斗中己方获得的净胜场次（指胜利场次减去失败场次）尽可能多。
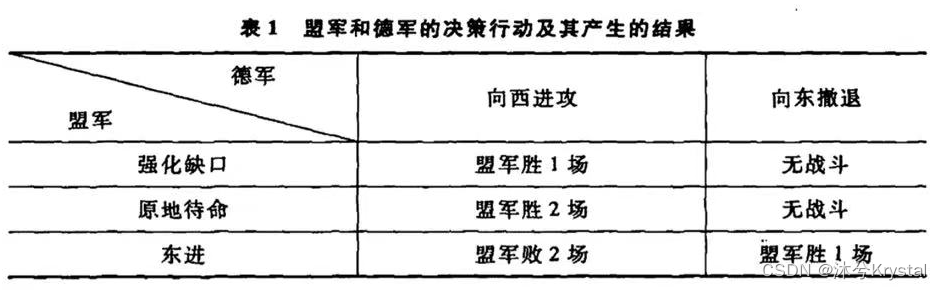
假设双方在决策时都知道以上信息，并且同时做出抉择，这种博弈称为完全信息静态博弈。
效用函数、赢得矩阵或支付矩阵
这种具有完全竞争性质，即一方所得正式对手所失的博弈，一般称为零和博弈。
在博弈中双方都力求通过决策行动使己方的效用函数最大化。

模型建立

参与博弈的双方用 $\left \{ 1,2\right \}$ 表示，1为盟军，2为德军。盟军可能的决策行动记作 $a_1\in A_1 = {1,2,3}$ ，德军的决策行动记作 $a_2\in A_2 = {1,2}$ 。

对于不存在纯纳什均衡的博弈问题，可以考虑双方随机地采取行动。
记盟军和德军的（混合）策略集分别为
$\begin{array}{c} S_{1}=\left\{p=\left(p_{1}, p_{2}, p_{3}\right) \mid 0 \leqslant p_{i} \leqslant 1, \sum_{i=1}^{3} p_{i}=1\right\}, \\ S_{2}=\left\{q=\left(q_{1}, q_{2}\right) \mid 0 \leqslant q_{i} \leqslant 1, \sum_{i=1}^{2} q_{i}=1\right\} \end{array}$
在混合策略下双方的效用函数用期望效用定义，记作
$U_{1}(\boldsymbol{p}, \boldsymbol{q})=\boldsymbol{p} M \boldsymbol{q}^{\mathrm{T}}=\sum_{i=1}^{3} \sum_{j=1}^{2} p_{i} m_{i j} q_{j}, U_{2}(\boldsymbol{p}, \boldsymbol{q})=-U_{1}(\boldsymbol{p}, \boldsymbol{q})$
双方的纯策略是有限的，其纯策略下的效用可以用矩阵描述，且双方的效用之和为0，这样的博弈称为二人零和矩阵博弈
通过占优性分析，可以降低问题的规模。

让报童订购更多的报纸

将报童和报社的利益放到一起考虑，研究怎样通过双方的博弈，让报童订购更多的报纸。
设报纸每份的订购价为 $w$ ，零售价为 $p$ ，未卖出的处理价为 $v$ ，期望销售量为：
$\begin{aligned} S(Q) &=\int_{0}^{Q} x f(x) \mathrm{d} x+\int_{Q}^{\infty} Q f(x) \mathrm{d} x \\ &=\left.x F(x)\right|_{0} ^{Q}-\int_{0}^{Q} F(x) \mathrm{d} x+Q(1-F(Q))=Q-\int_{0}^{Q} F(x) \mathrm{d} x \end{aligned}$
最优订货量如下式子：
$F\left(Q_{r}\right)=\frac{p-w}{p-v}$
报社和报童的决策可以通过如下的两阶段动态博弈模型来描述：第一阶段，由报社决定批发价 $w$ ，第二阶段，由报童决定订货量 $Q$ .
动态博弈一般通过反向归纳法求解。首先考虑第二个阶段的问题，得到报童的最优反应，再考虑阶段一，得到战略组合以达到子博弈完美均衡。
如果将报童和报社的利益放到一起考虑，得到 $Q^*$ 作为报童的最优订购量，寻求使报社和报童双方利益达到协调的途径。最常用的办法之一是通过谈判达成对双方具有约束力的协议。

价格折扣协议模型

4. 概率模型

如果随机因素对研究对象的影响必须考虑，就应该建立随机性的数学模型。

传送系统的效率

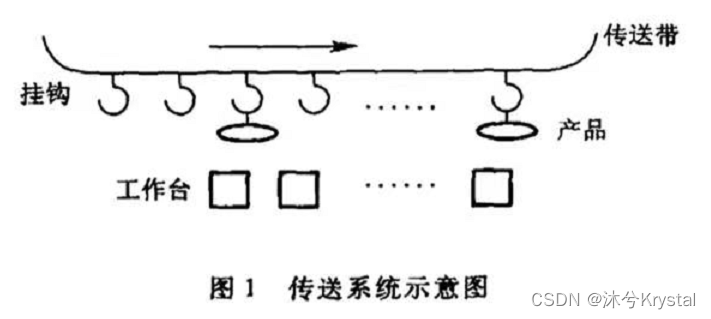
在这里插入图片描述

构造一个衡量传送系统效率的指标。

模型假设

有n个工人，他们的生产是相互独立的，生产周期是常数，n个工作台均匀排列；
生产已进入稳态，即每个工人生产出一件产品的时刻在一周期内是等可能的；
在一周期内有m个钩子通过每一工作台上方，钩子均匀排列，到达第一个工作台上方的钩子都是空的；

模型建立

将传送系统效率定义为一周期内带走的产品数与生产的全部产品数之比，记作 $D$ .
从钩子的角度考虑，若能对一周期内 m 只钩子求出每只钩子非空（即挂上产品）的概率 p，则带走的产品数 $s = m p$ 。
得到 p 的步骤如下：
任一钩子被一名工人触到的概率是 $\frac{1}{m}$
由工人生产的独立性，任一钩子为空钩的概率是 ${\left ( 1-\frac{1}{m} \right ) }^n$
所以 $p=1-\left(1-\frac{1}{m}\right)^{n}$
故传送系统效率指标为
$D=\frac{m p}{n}=\frac{m}{n}\left[1-\left(1-\frac{1}{m}\right)^{n}\right]$
此模型是在理想情况下得到的，模型的意义在于利用基本合理的假设将问题简化到能够建模的程度，并用很简单的方法得到结果。

报童的诀窍

报纸每份的购进价为 b，零售价为 a，退回价为 c，为报童筹划一下，应如何确定每天购进报纸的数量，以获得最大的收入。
每天报纸的需求量为 r 份的概率是 $p (r) (r = 0, 1, 2...)$ ，以此建立关于购进量的优化模型
优化模型的目标函数，不能是报童每天的收入，而应是报童每天收入的期望值，简称平均收入。记报童每天购进 n 份报纸的平均收入为 $G (n)$ ，问题归结为在 $f (r), a, b, c$ 已知时，求n使 $G (n)$ 最大
$G(n)=\int_{0}^{n}[(a-b) r-(b-c)(n-r)] p(r) \mathrm{d} r+\int_{n}^{\infty}(a-b) n p(r) \mathrm{d} r$
求导得到：
$\begin{aligned} \frac{\mathrm{d} G}{\mathrm{~d} n} &=(a-b) n p(n)-\int_{0}^{n}(b-c) p(r) \mathrm{d} r-(a-b) n p(n)+\int_{n}^{\infty}(a-b) p(r) \mathrm{d} r \\ &=-(b-c) \int_{0}^{n} p(r) \mathrm{d} r+(a-b) \int_{n}^{\infty} p(r) \mathrm{d} r \end{aligned}$
令 $\frac{\mathrm{d} G}{\mathrm{d} n}=0$ ，得到
$\frac{\int_{0}^{n} p(r) d r}{\int_{n}^{\infty} p(r) d r}=\frac{a-b}{b-c}$
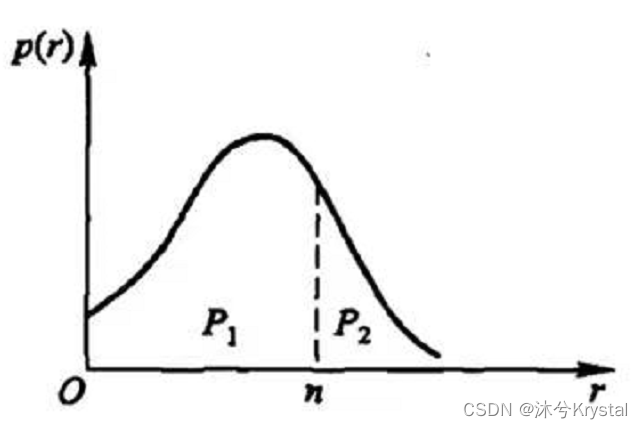
$P_1$ 是卖不完的概率（需求量小于购进量）， $P_2$ 是卖完的概率，故：
$\frac{P_{1}}{P_{2}}=\frac{a-b}{b-c}$
表明，购进的份数 $n$ 应该使得卖不完与卖完的概率之比，恰好等于卖出一份赚的钱与退回一份赔的钱之比。