机器学习系列05：支持向量机

支持向量机简称为 SVM（Support Vector Machine）。

基础名词解释

首先了解几个名词，决策边界（Decision boundary）就是划分分属不同类别样本的超平面，非常靠近决策边界的训练样本称为支持向量（Support vector），每个类别中的支持向量又形成了不同的超平面（Hyperplane），这些超平面之间的又形成了天然的间距（Margin）。

下面的三条虚线都将红蓝样本分割开了，可是哪种分割最好？

SVM 不仅要将红蓝样本分割开，而且还会形成一条使得 margin 尽可能大的决策边界。margin 越大，表示模型的泛化性能（指模型在测试集上的表现）越好，margin 越小，则可能引发过拟合问题。

SVM 中也有一个参数 C，C 越大，则表示对错误分类的惩罚越大，C 越小，则表示对错误分类的惩罚越小。

Iris 数据集进行分类

还是同样的使用 scikit-learn 实现的 SVM 对 Iris 数据集进行分类。

在实际的分类任务中，《机器学习系列04：逻辑回归》中提到的线性逻辑回归和线性 SVM 通常会产生相似的结果，但是逻辑回归模型比 SVM 要简单，其背后的数学原理易于解释和理解。

那么为什么还要有 SVM 呢？

因为我们可以通过 SVM 的核方法解决线性不可分问题。我们无法用一条直线（或者曲线）将红蓝样本分割开：

所谓的核方法就是通过一个函数将当前空间上线性不可分的数据集映射到一个高维空间上，在这个高维空间上，数据集是线性可分的：

我们可以通过 kernel 参数指定这个映射函数，目前默认的映射函数就是 rbf（也称为高斯核）：

再用 rbf 核来处理 Iris 数据集

这里我们又见到了一个 gamma 参数，它控制着决策边界的圆滑程度，让我们增大 gamma 看看：

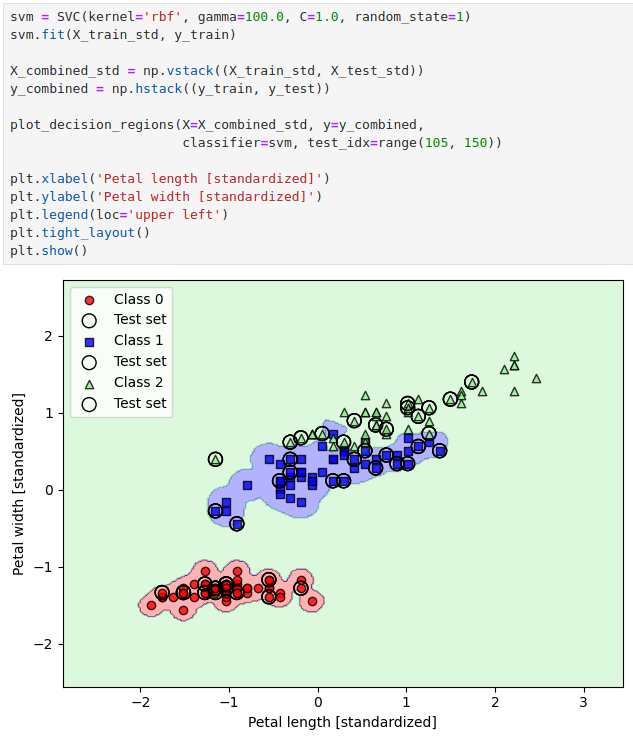
虽然看到训练集中的样本被近乎完美地切分开了，但是这样的模型无疑会过拟合。

这也说明了 gamma 参数在控制模型过拟合和欠拟合方面也有重要作用。