Machine Learning week1

**

监督学习Supervised Learning

**
定义A：给出一个算法，需要部分数据集已经有正确答案，比如给定房价数据集，对于里面的每个数据，算法都知道对应的正确房价，算法的结果就是算出更多的正确价格。
定义B：监督学习又称回归问题Regression Problem，意指要预测一个连续值的输出。
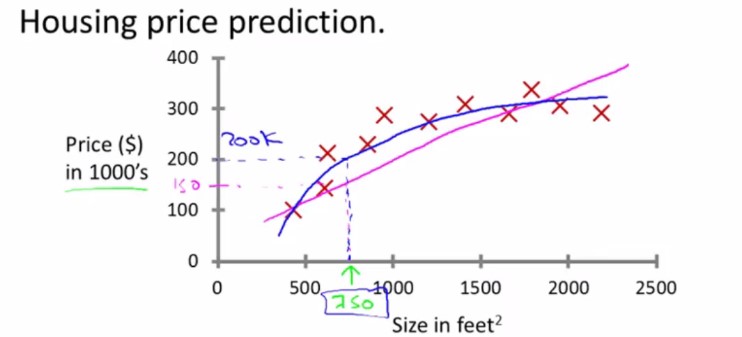
监督学习（回归问题）：房价预测

监督学习（分类问题）：肿瘤预测

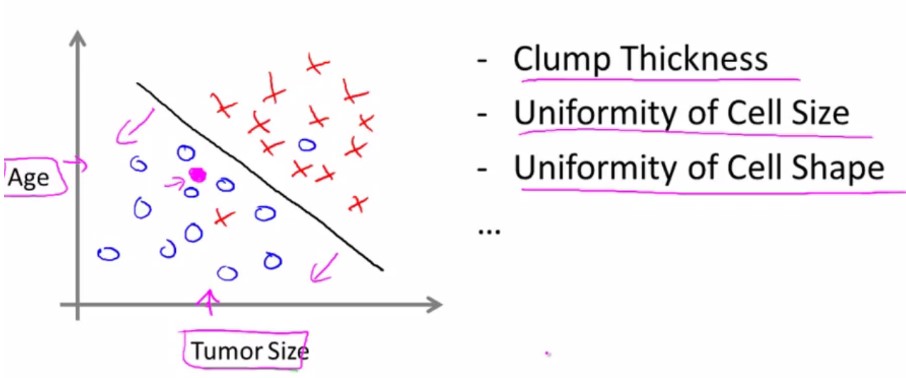
监督学习中，对于数据集中的每个数据，都有相应的正确答案，算法就是基于这些来作出预测。
监督学习：A、回归问题，B、分类问题
回归问题(Regression)：通过回归来根据之前的数据预测一个连续型输出（预测房价，房价精确到美分，所以是连续型数值）
分类问题(Classification)：预测离散型输出（预测肿瘤：无、A肿瘤、B肿瘤、C肿瘤）

无监督学习Unsupervised Learning

在无监督学习中，没有属性或标签这一概念，所有的数据都是一样的没有区别，在无监督学习中，我们只有一个数据集，没人告诉我们该怎么做。
现在的问题是：现在有一个数据集，你能在其中找到某种结构吗？
对于给定的数据集，无监督学习算法可能判定该数据集包含两个不同的聚类，无监督学习算法会把这些数据分成两个不同的聚类，这就是“聚类算法”。

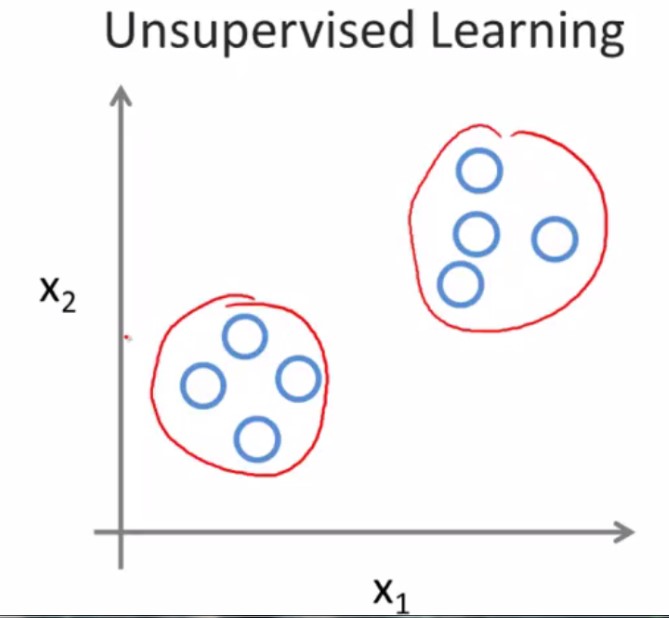
举个栗子：谷歌新闻搜索成千上万的新闻然后自动的将他们聚合在一起，所以有关同一主题的新闻被显示在一起。
无监督学习：这里有一堆数据，我不知道这些数据是什么，里面有哪些类型，叫什么名字，但是请你自动找到这些数据中的类型，然后按照得到的类型把这些个体分类。让算法自己从数据中发现一切。
无监督学习：1、聚类算法 2、鸡尾酒会算法
无监督学习（聚类算法）的适用场景：管理计算机集群、社交网络分析、市场细分、天文数据分析
无监督学习（鸡尾酒会算法）： 用于将混杂在一起的来自不同声源的声音分类出来。
监督学习–>线性回归算法
Linear Regression with one variable（单变量线性回归）

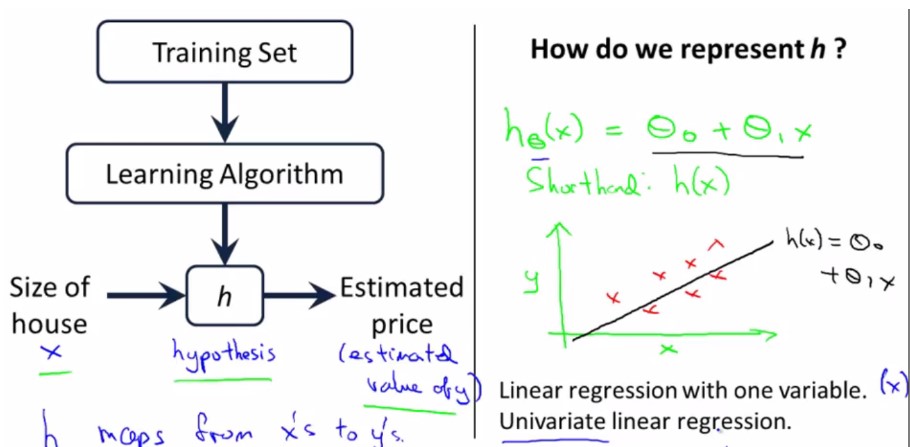
theta0和theta称为parameter（模型参数）
Cost Function(代价函数)（平方误差代价函数）
正规写法如下：


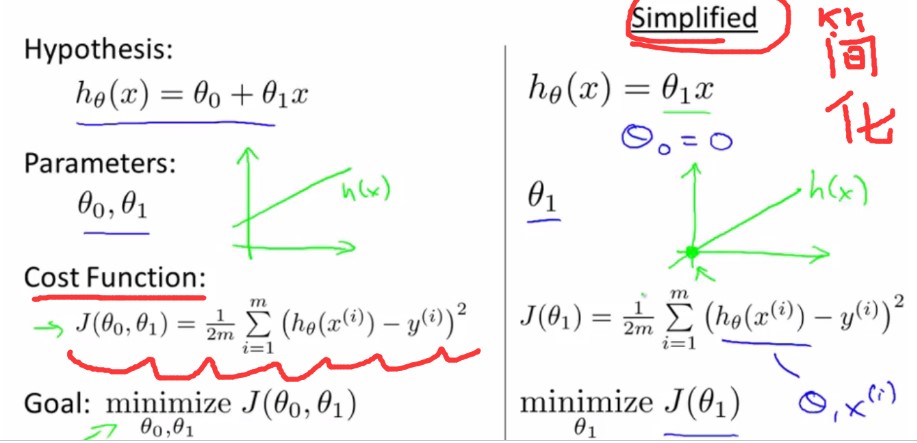
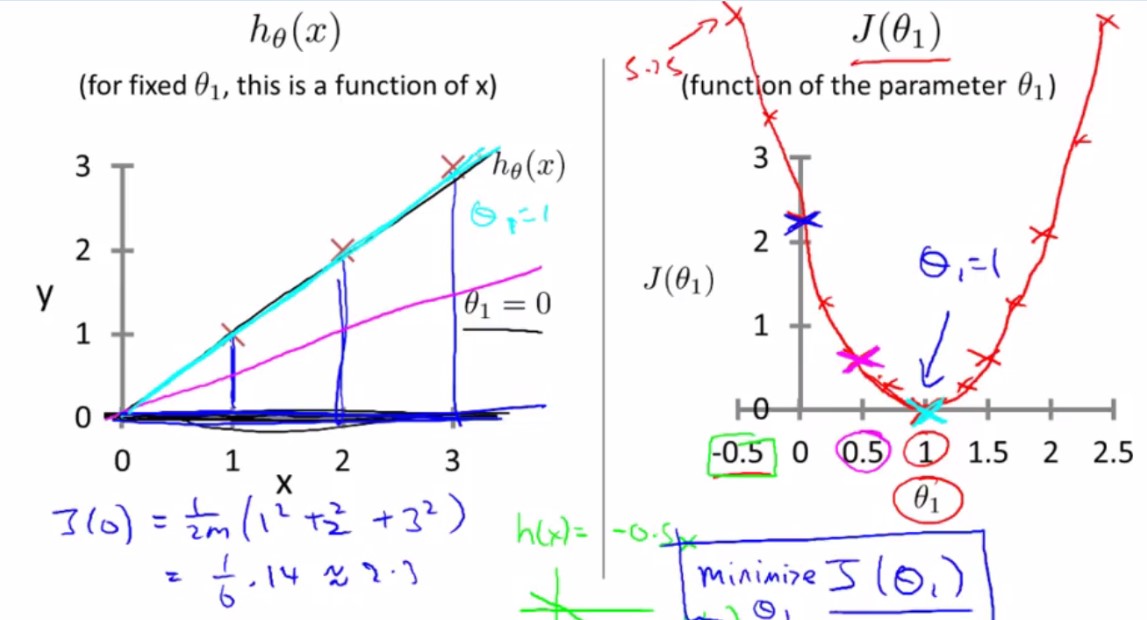
将theta0=0，h(x)=theta1X来简化问题，方便理解CostFunction与（hypothesis）h(x)的关系，为什么求出CostFunction的minimize对应着最佳的h(x)拟合曲线？
h(x)=theta0+theta1X当theta0==0的时候，CostFunction J(theta)的图像是一个二维图：

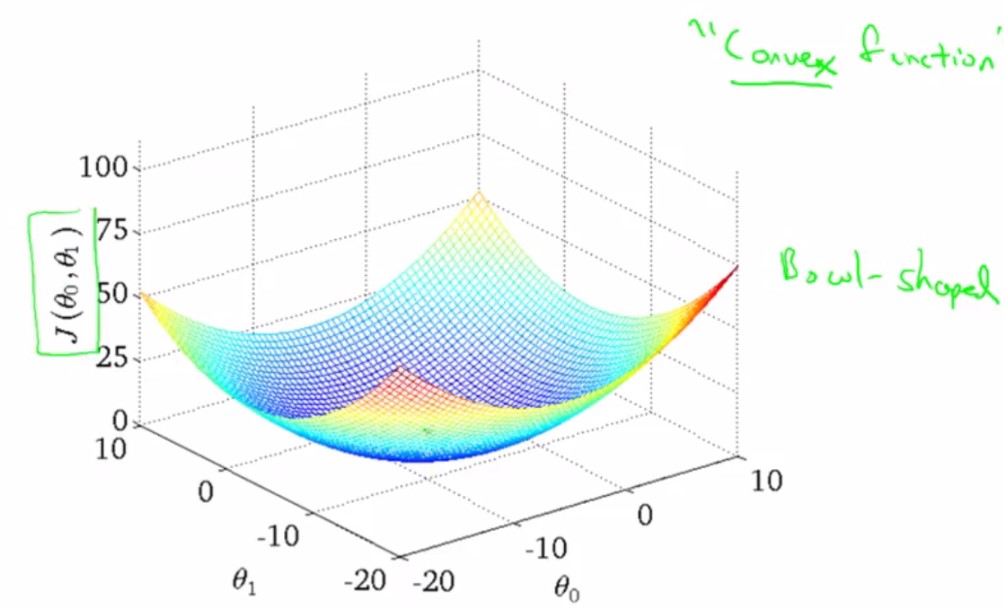
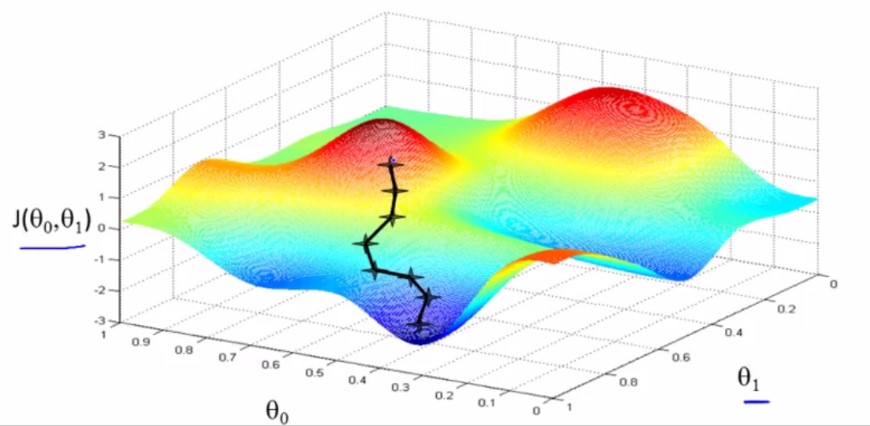
h(x)=theta0+theta1X当theta0!=0的时候，CostFunction J(theta)的图像是一个三维图：

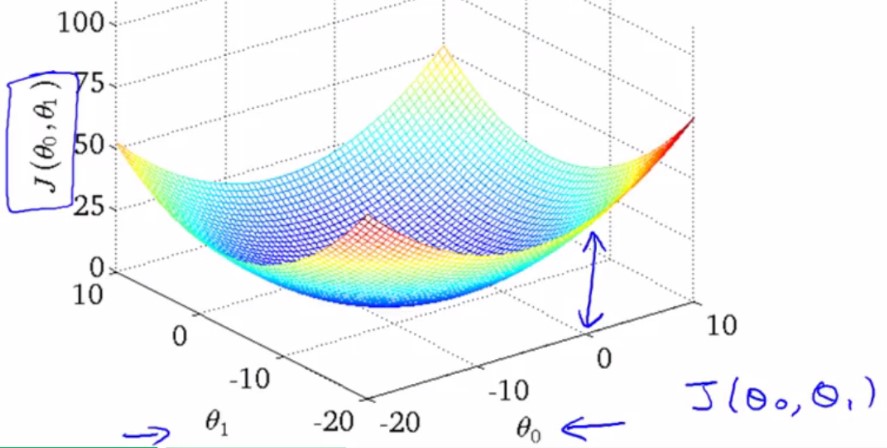
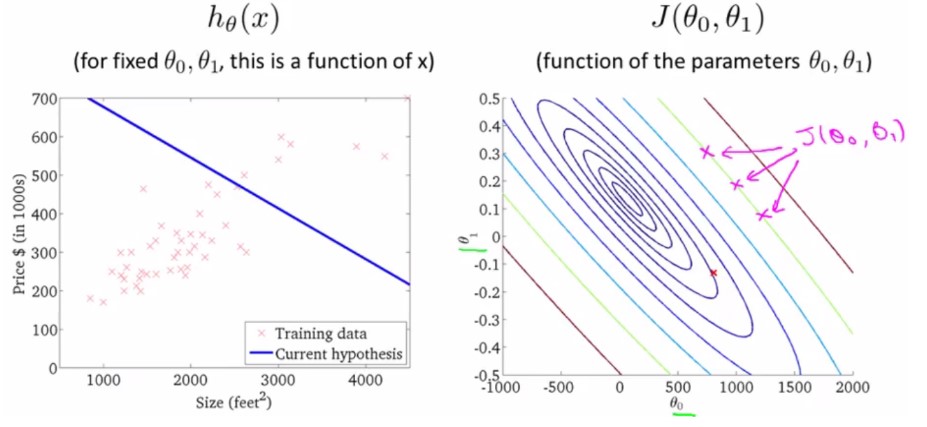
将该三维图转换为二维的轮廓图（轮廓图上面的红X对应着左边的h(x)直线，轮廓图最中央的椭圆中心代表min(J(x))，即最小的代价函数）：

梯度下降法（Gradient descent）
梯度下降法可以使代价函数J最小化

令theta0=0，则h(theta)=theta1*x，代价函数为J(theta1)为关于theta1的二维函数，画出的图像也是二维的，将问题简单化来更直观的理解梯度下降法：

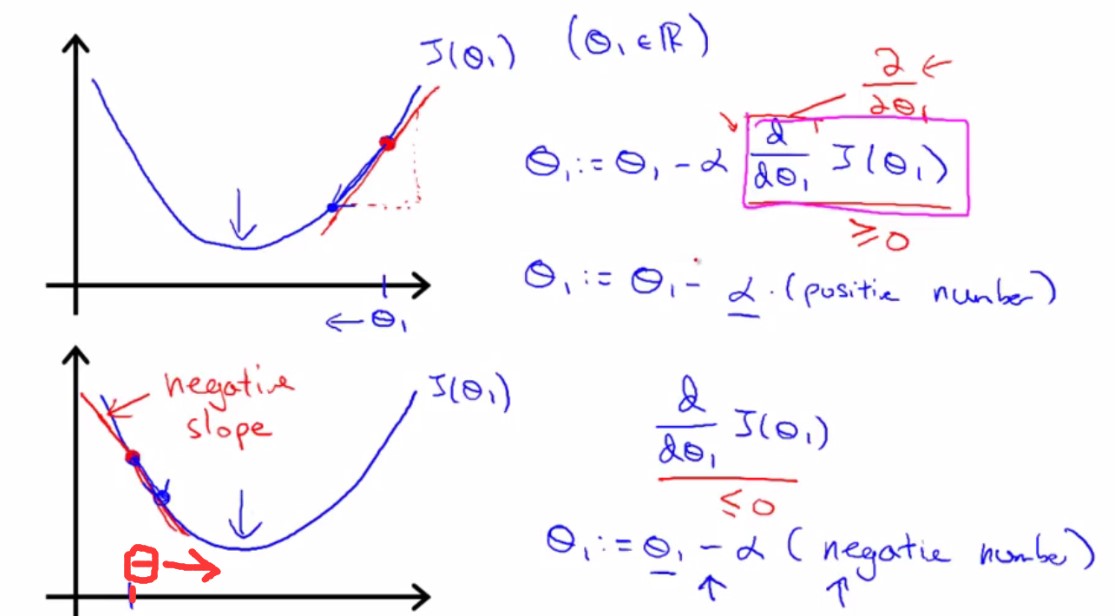
如图所示，学习速率阿尔法>0，当选取的初始点在min点的右边时，初始点的切线斜率>0，阿尔法切线斜率>0，所以theta1=theta1-正数，theta1变小，向min点靠近。反之，当选取的初始点在min点的左边时，初始点的切线斜率<0，阿尔法切线斜率<0，所以theta1=theta1-负数，theta1变大，向min点靠近。
如此一步步的更新，theta1将慢慢靠近以至于到达min点。

学习速率阿尔法的大小对梯度下降的影响：

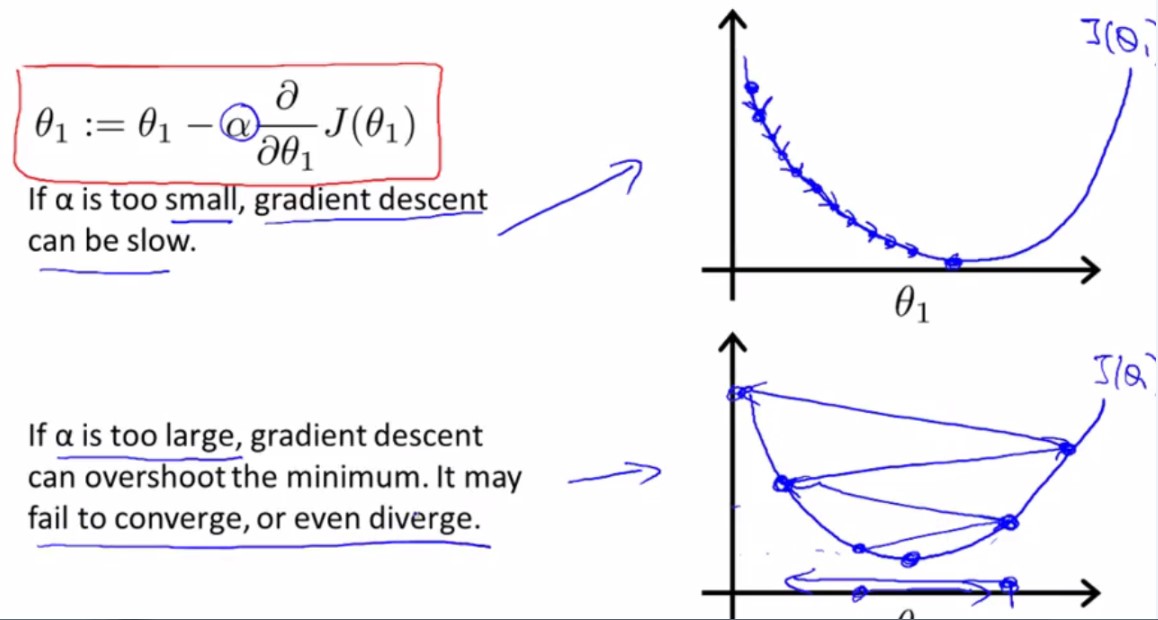
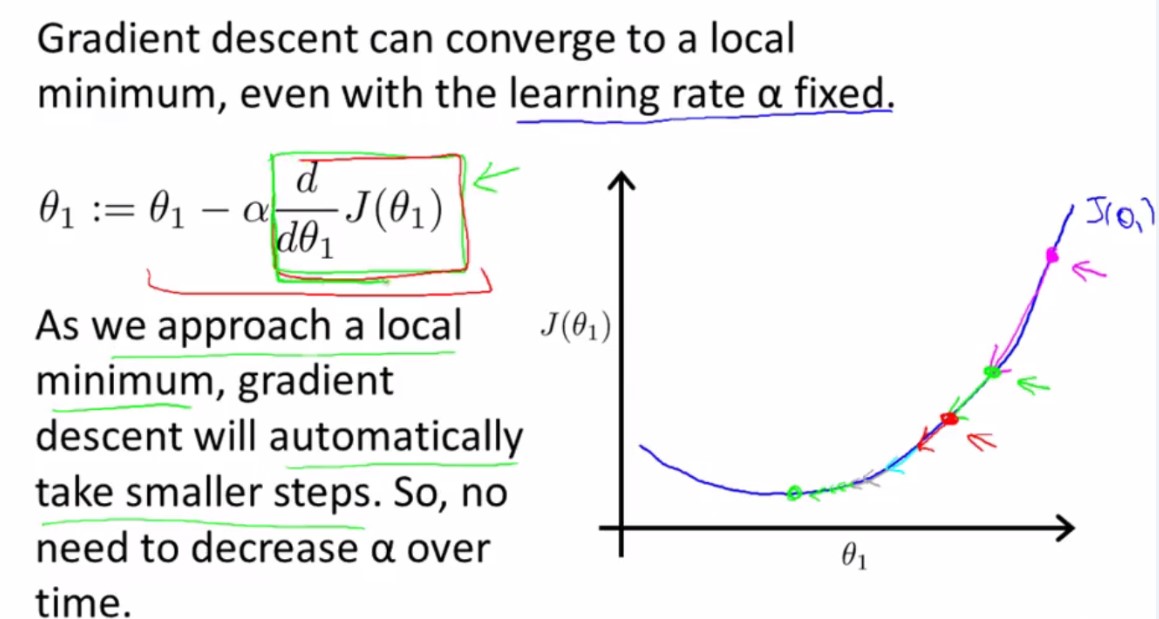
假设将theta1初始化在局部最低点，那么使用梯度下降法theta1不会移动。因为切线斜率为0，所以d/(d*theta1)*J(theta1)=0，theta1 := theta1 - 0，原地维持不变。

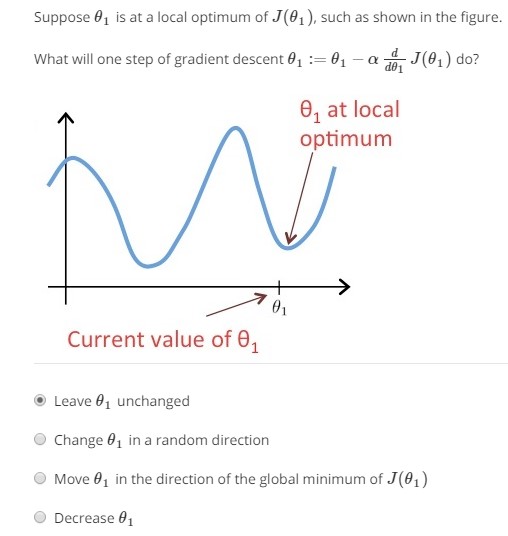
随着梯度下降法的进行，theta1越来越接近最小值，在图形上表现为越来越接近最低点，其斜率也越来越小，所以在后续的每次梯度下降中，越接近最低点，梯度下降法自动采取较小的幅度（步伐）。所以保持学习速率阿尔法不变的情况下，梯度下降法可以聚合到局部最小值。

将梯度下降法与线性回归方程结合在一起（使用梯度下降法来计算出线性回归方程的最优解）
公式推导：

因为线性回归方程的代价函数是一个凸函数（convex function），所以这个函数没有局部最优解，只有一个全局最优解。所以对这种代价函数使用线性回归的梯度下降法得到的结果总是收敛到全局最优值，因为除了全局最优以外没有其他的局部最优点。

这里写图片描述
批量梯度下降（batch gradient descent）：在梯度下降的每一步，我们都用到了所有的训练样本。