豆瓣9.5，陶哲轩最经典专业数学著作，徒手搭建起数学大厦！读者盛赞“连附录A都写得这么精彩”...

说到数学领域的经典图书，你可能会在脑海中列出很多。比如图灵就出版过《普林斯顿微积分读本》《具体数学》《线性代数应该这样学》等等。今天我们要说的这本，也是一本数学领域的超级经典，它就是“数学界的莫扎特”、智商超过220、UCLA数学系终身教授，最年轻菲尔兹奖得主——陶哲轩的作品《陶哲轩实分析》。

豆瓣读者评价”为什么读？1.第一章就告诉你了，分析是算的基础，不明白分析原理又盲目的算，可能导致灾难性的的后果；2.分析是一种思维方式，严格性很美；3.知道数学大厦是如何一砖一瓦建立的；4.当然是为了更深入学习概率“

这本书新版和老版都在豆瓣有着9.5的高分，是一本不可多得的经典之作！

《陶哲轩实分析（第3版）》

作者：[澳]陶哲轩（Terence Tao）

译者：李馨

文 | 引言

什么是分析

本书将介绍高等实分析，这是关于实数、实数序列、实数级数以及实值函数的分析。虽然实分析与复分析、调和分析以及泛函分析是相关的，但与它们又是不同的。复分析是关于复数和复函数的分析；调和分析是关于调和函数（振动）的分析，比如正弦振动，并研究这些函数如何通过傅里叶变换构造其他函数；泛函分析研究的内容主要集中在函数上（以及这些函数如何构造出如向量空间这样的东西）。分析学是对这些对象进行严格研究的学科，并且着力于对这些对象做出准确的定性和定量分析。实分析是微积分学的理论基础，而微积分是我们在处理函数时所用到的计算规则的集合。

在本书中，我们将对很多概念进行研究，而这些概念在学习初等微积分时会学到，比如：数、序列、级数、极限、函数、定积分、导数等。虽然你曾经基于这些概念进行过大量的运算，但是现在我们主要研究这些概念的基本理论。我们关心如下几个问题。

（1）什么是实数？是否存在最大的实数？“0”之后的“下一个”实数是多少？（即：最小的正实数是几？）是否能够对一个实数进行无限次分割？为什么有些数（比如 2）有平方根，而有些数（比如-2）没有平方根？如果有无穷多个实数和无穷多个有理数，那么为什么会说实数比有理数的个数“多”？

（2）如何确定实数序列的极限值？什么样的序列存在极限，什么样的序列不存在极限？如果你能够阻止一个序列趋向无穷，这是否意味着该序列最终会停止变化并且收敛？把无穷多个实数相加后得到一个有限实数的情况是否存在？把无穷多个有理数相加后得到一个非有理数的情况是否存在？如果有无穷多个数相加，那么改变这些数的排列次序，所得到的和是否保持不变？

（3）什么是函数？函数是连续的、可微的、可积的、有界的分别是什么意思？能否将无限多个函数相加？对函数序列取极限会怎样？能否对无穷函数级数求微分？什么是求积分？如果一个函数 f(X) 满足：当 x=0 时，f(X) 的值为3 ；当 x=1 时，f(X) 的值为 5（即f(0)=3 且f(1)=5），那么 x 若取遍 0 到 1 之间的所有值，f(X)是否也取遍了3 到 5 之间的所有值? 为什么?

如果你上过微积分课程，也许能够回答出上述问题中的几个。但是对于微积分这类课程来说，上述这类问题并不是最重要的。这类课程的重点在于教会学生如何计算，比如计算函数 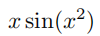从 x=0 到 x=1上的积分。既然现在你对这些概念已经非常熟悉了，而且知道如何进行运算，那么我们将回归到理论知识并且尝试真正去理解这些内容是如何展开的。

为什么要做分析

当人们谈论分析理论的时候，自然会想到“为什么要做分析”这个问题。从哲学角度来说，认识到事物为什么起作用，能够带给人们一定的满足感。但是，讲究实际的人会认为，只需要了解事物在解决实际问题时是如何起作用的就足够了。在学习入门课程时，你曾经接受过的微积分训练，足以让你可以开始着手解决存在于物理、化学、生物、经济、计算机科学、金融、工程学或者其他学科中的问题。而且，对于链式法则、洛必达法则或者分部积分法等，即使你并不了解它们为什么会起作用，或者不知道这些法则是否有例外的情况存在，也不影响你应用它们来解决问题。然而，如果一个人在应用某些法则时并不了解它们是如何得出的，也不知道使用这些法则有哪些限制条件，那么他将陷入困境之中。我来举一些例子。这些例子将告诉我们，对于那些我们熟知的法则，如果不了解其背后潜在的分析原理而盲目地应用它们，将会导致灾难性的后果。

例 1.2.1（用零做除数） 这是大家都非常熟悉的一个例子。当 c=0 时，消去律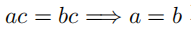不成立。例如，等式 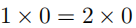是恒成立的，但是如果有人盲目地消去 0，那么将会得到1=2，这显然是错误的。在这个例子中，能够明显看出错误在于用零做了除数；但是在其他情况下，错误可能更加隐蔽。

例 1.2.2（发散级数） 你也许见过如下无穷和形式的几何级数：

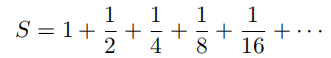
你大概也见过按照下面的技巧求该级数和的方法：令该级数和为S，那么将等号两端同时乘以 2 得

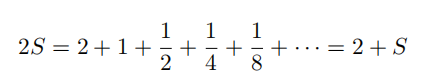
于是 S=2，因此上述级数和为2。但是，如果按照同样的方法来计算级数：

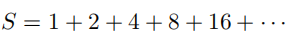
将得到一个荒谬的结果：

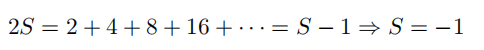
那么，按照同样的计算方法，我们得到了 

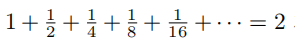
 和 1 + 2 + 4 +8 + · · · = −1两个结果。为什么我们认为前一个等式是成立的，而第二个等式是不成立的？另外一个类似的例子是关于下面这个级数的：

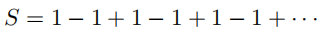
该级数可以写成如下形式：

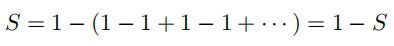
于是 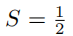 ；另外，我们也可以这样写：

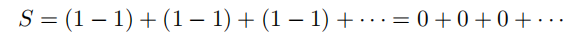
于是 S=0 ；或者，我们也可以这样写：

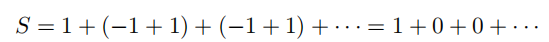
于是S=1。那么上述三个结果，究竟哪一个才是正确答案呢？（答案见习题 7.2.1。）

例 1.2.3（发散序列） 在这里，我们对之前的例子做出一些小的变动。x 表示一个实数，L 表示极限：

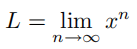
做变量替换 n=m+1，我们可以得到：

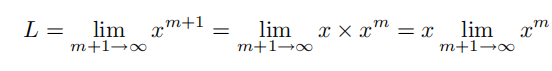
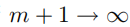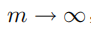若 ，则有 ，因此：

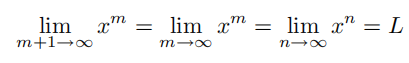
于是：

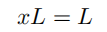
此时，消去 L可得，对任意实数 x，均有x=1。这显然是非常荒谬的。但是，由于我们已经意识到之前“用零做除数”的错误，此时可以更聪明些，并推导出要么x=1，要么 L=0。特别地，我们似乎已经证明了这样一个结论:对任意的实数 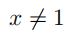，均有：

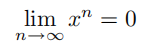
但是，当 x 取某些特定值时，上述结论是荒谬的。比如，当 x=2时，我们能够推导出序列 1, 2, 4, 8, · · · 是收敛于 0 的；当x=-1 时，序列 1, −1, 1, −1, · · ·也是收敛于 0的。这些结论看起来非常荒谬。上述论证出现了什么样的问题呢？（答案见习题 6.3.4。）

例 1.2.4（函数的极限值） 对于极限表达式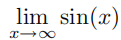，我们做变量替换x =y + π，并且根据等式 

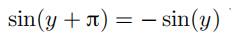
可以得到：

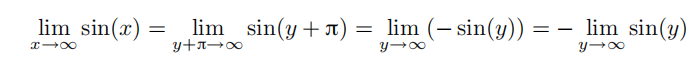
又因为

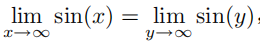，所以得出：

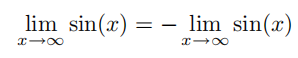
因此：

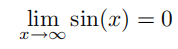
如果我们对上式做变量替换 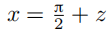，那么根据

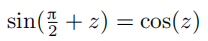
 可得：

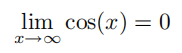
分别对上述两个极限求平方，然后将它们相加可得：

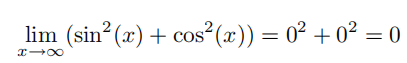
另外，我们知道对任意的实数 x，

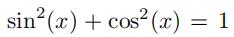
 恒成立。于是，我们得到 1=0! 这里究竟存在什么样的难点呢？

例 1.2.5（交换求和次序） 我们考虑有关运算的如下事实。对任意的数值矩阵，例如：

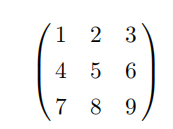
计算该矩阵的每一行元素之和以及每一列元素之和，然后分别把所有行的和相加、所有列的和相加。最后，你会发现上述两种运算的结果是相等的——都等于矩阵中所有元素相加的和：

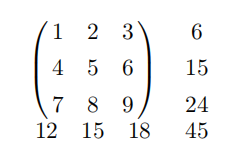
换言之，如果你想要将一个 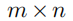矩阵中的所有元素相加，那么不管你是先把每一行的元素加起来，还是先把每一列的元素加起来，最后得到的结果都是一样的。（在计算机被发明出来之前，会计师和簿记员在结算账目的时候，都会采用这种方法来避免错误。）用级数的概念来描述以上事实即为：

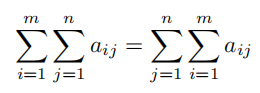
其中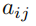， 表示矩阵的第 i 行第 j 列元素。

现在，有人可能会认为上述结论应该很容易推广到无穷级数：

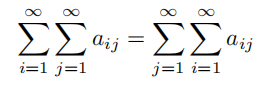
实际上，如果你在工作中很多地方都会用到无穷级数，那么你会发现自己经常像这样通过变换次序来求和。也就是说，在一个无穷矩阵中，行和相加的结果与列和相加的结果是一样的。然而，尽管这种说法听起来合理，但它实际上是错误的！这里给出一个反例：

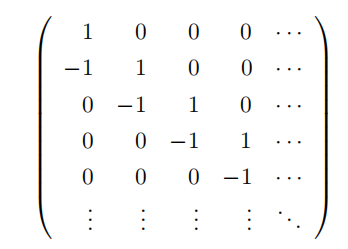
如果你对该矩阵每一行元素求和，然后将得到的所有行和相加，那么你会得到1。但是，如果你对该矩阵每一列元素求和，然后将得到的所有列和相加，那么你会得到0 !因此，这是否意味着对无穷级数求和不能采用交换次序的方法，而且任何采用交换次序方法所得到的结论都是不可信的？（答案见定理 8.2.2。）

例 1.2.6（交换积分次序） 交换积分次序与交换求和次序一样，都是数学中很常见的运算技巧。假设我们想要计算某个曲面 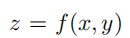之下的体积（此处我们暂时不考虑积分上下限）。一种方法是平行于 x 轴进行切割：对任意给定的 y，我们能够计算出与之对应的一部分面积为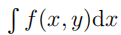， 然后我们把这部分以 y 为变量的面积进行积分就得到了要求的体积：

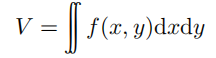
或者，对于任意给定的 x，我们也可以平行于 y 轴进行切割，并且计算出与 x 对应的一部分面积为 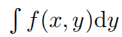， 然后沿 x轴对上述面积进行积分，从而得到体积为：

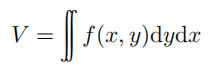
这似乎表明我们可以通过交换积分号来运算：

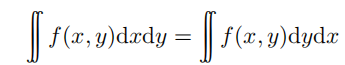
事实上，因为有时先对某个变量进行积分要比先对其他变量进行积分更加容易，所以人们往往采用交换积分号的方法来运算。但是，正如前文中对无穷个元素求和有时不能交换求和次序一样，交换积分号的运算有时也会存在风险。下面给出一个关于被积函数 

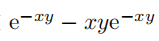
 的例子。假设该积分是可以交换积分号的：

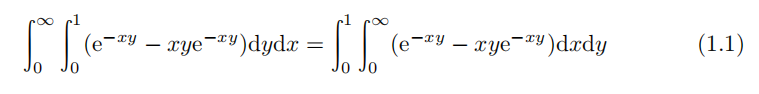
因为

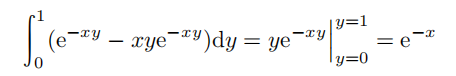
所以式 (1.1) 的等号左侧表达式为 

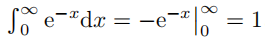
。但是，又因为

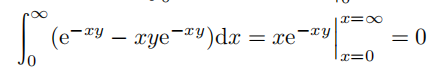
所以式 (1.1) 的等号右侧表达式为 

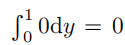
。显然 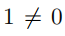，因此上文中的某处存在错误；然而你会发现，除了交换积分号这一步骤，上面的过程并不存在其他的错误。那么，我们如何判断什么时候可以放心地进行交换积分次序的运算呢？（定理 19.5.1 会给出部分答案。）

例 1.2.7（交换极限运算次序） 我们考虑下面这个看似正确的表达式：

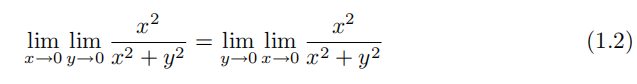
因为我们有

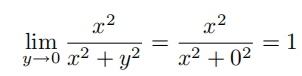
所以式 (1.2) 等号左侧表达式等于1；另外，我们知道

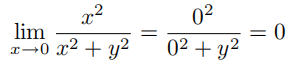
因此，式 (1.2) 等号右侧表达式等于 0。由于 1显然不等于 0，所以这表明了交换极限运算次序是不可信的。然而，是否存在某些情况，交换极限运算次序能够成立呢？（习题 14.3.2 给出了部分答案。）

例 1.2.8（再谈交换极限运算次序） 考虑如下貌似正确的表达式：

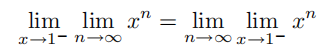
其中，记号 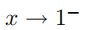 表示 x 从 1 的左侧趋向于 1。当 x 在1 的左侧时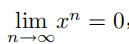，，因此上面等式的左端等于 0。但是对于任意给定的n，我们总可以得到 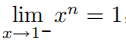，因此，上面等式右端的极限值为 1。这是否意味着这种类型的极限运算次序交换都是不可信的？（答案见命题 14.3.3。）

例 1.2.9（交换极限运算与积分运算的次序） 对任意的实数 y，我们有

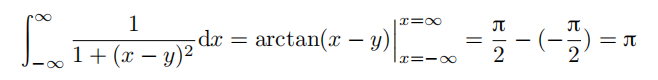
当 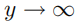 时取极限， 我们可以得到：

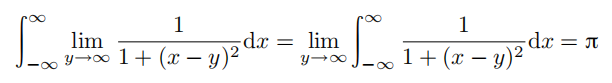
但是对于任意 x，我们有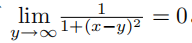。因此，我们似乎可以推导出 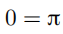。上述论证出现了什么问题？是否应该舍弃（非常有用的）交换极限运算与积分运算次序的技巧？（定理 14.6.1 给出了部分答案。）

本书中的分析理论将帮助你解决以上这些问题，并且会让你了解这些法则（以及其他的法则）在什么情况下是适用的，在什么情况下是不能使用的，从而把这些法则有益的应用与谬论隔离开来。所以，分析理论可以避免你犯错，并且有助于你在更广泛的领域中应用这些法则。

此外，在你不断深入学习分析理论的同时会培养一种“分析的思维方式”。当涉及数学中一些新的法则或者处理某些标准法则无法应用的情况时，这种思维方式将对你有所帮助。

例如，如果函数是复值的而不是实值的，将会发生什么样的情况？假如你现在处理的是一个球面而不是平面，情况会如何？如果你面对的函数不是连续的，而是类似于矩形波和 δ函数之类的函数，那应该是什么样的情况？若你处理的函数、积分上下限或者求和上下限偶尔成为无穷的，情况将如何？你将会感知到为什么某个数学法则（如链式法则）能够起作用，如何把该法则应用到其他新的情况中，该法则的使用有哪些限制条件（如果存在限制条件的话）；这会让你更加自信地、准确地使用已经学到的数学知识。

01

《陶哲轩实分析（第3版）》

作者：[澳]陶哲轩（Terence Tao）

译者：李馨

本书源自华裔天才数学家、菲尔兹奖得主陶哲轩在加州大学洛杉矶分校教授实分析课程的讲义。

全书从分析的源头——数系的结构和集合论开始，然后引向分析基础，再进入幂级数、多元微分学和傅里叶分析，最后介绍勒贝格积分，几乎完全是以具体的实直线和欧几里得空间为背景，完美结合了严格性和直观性。

02

《陶哲轩教你学数学》

作者：陶哲轩

译者：李馨

菲尔兹奖得主陶哲轩数学思维大解析，通过奥数竞赛习题解答，带你领悟数学之美。

本书是国际知名数学家陶哲轩15岁时的著作，从青少年的角度分析数学问题，主要是数学竞赛等智力谜题，用学生的语言解释思考过程，完整展现了少年陶哲轩的解题思路。