LESSON 12.8 原理进阶 (1)：GBDT数学流程与残差概念辨析

四 原理进阶：GBDT的求解流程

1 GBDT的基本数学流程

作为当代众多经典算法的基础，GBDT的求解过程可谓十分精妙，它不仅开创性地舍弃了使用原始标签进行训练的方式，同时还极大地简化了Boosting算法的运算流程，让Boosting算法本该非常复杂的运算流程变得清晰简洁。当我们学过完整的AdaBoost流程后，我们会发现GBDT的数学流程非常简明、美丽，同时这一美丽的流程也是我们未来所有Boosting高级算法的数学基础。与任意Boosting算法一致，对GBDT我们需要回答如下问题：

• 损失函数$L(x,y)$的表达式是什么？损失函数如何影响模型构建？
• 弱评估器$f(x)$ 是什么，当下boosting算法使用的具体建树过程是什么？
• 综合集成结果$H(x)$是什么？集成算法具体如何输出集成结果？

同时，还可能存在其他需要明确的问题，例如：

• 是加权求和吗？如果是，加权求和中的权重如何求解？
• 训练过程中，拟合的数据$X$与$y$分别是什么？
• 模型训练到什么时候停下来最好？

对于GBDT，由于我们存在提前停止机制以及资源控制，因此我们一般不去在意模型停止相关的问题，但除此之外的每个问题我们都需要仔细研究。

回顾Boosting算法的基本指导思想，我们来梳理梯度提升树回归算法的基本流程。虽然Boosting理论很早就被人提出，但1999年才是GBDT算法发展的高潮。1999年，有四篇论文横空出世：

• 《贪心函数估计：一种梯度提升机器》
  
  Friedman, J. H. (February 1999). “Greedy Function Approximation: A Gradient Boosting Machine”

• 《随机梯度提升》
  
  Friedman, J. H. (March 1999). “Stochastic Gradient Boosting”

• 《梯度下降式提升算法》
  
  Mason, L.; Baxter, J.; Bartlett, P. L.; Frean, Marcus (1999). “Boosting Algorithms as Gradient Descent”

• 《函数空间中的梯度下降式提升算法》
  
  Mason, L.; Baxter, J.; Bartlett, P. L.; Frean, Marcus (May 1999). “Boosting Algorithms as Gradient Descent in Function Space”

今天我们学习的GBDT算法是融合了上述4篇论文思想的集大成之作。本次我们将基于sklearn中实现的GBDT来梳理数学流程，但不同的数学流程可能来自于上述不同的论文。需要注意的是，为了与之前课程中的符号表达相一致，我们将使用与原论文不同的符号，但数学过程将是完全相同的。

假设现有数据集$N$，含有形如$(x_i,y_i)$的样本$M$个，$i$为任意样本的编号，单一样本的损失函数为$l(y_i,H(x_i))$，其中$H(x_i)$是$i$号样本在集成算法上的预测结果，整个算法的损失函数为$L(y,H(x))$，且总损失等于全部样本的损失之和：$L(y,H(x))={\sum }_{i}l(y_i,H(x_i))$。同时，弱评估器为回归树$f$，总共学习$T$轮。则GBDT回归的基本流程如下所示：

1）初始化数据迭代的起点$H_0(x)$。sklearn当中，我们可以使用0、随机数或者任意算法的输出结果作为$H_0(x)$，但在最初的论文中，Friedman定义了如下公式来计算$H_0$：

$$\begin{array}{rl}{H}_0(x)& =\underset{C}{\mathrm{argmin}}\sum _{i=1}^{M}l\left(y_i,C\right)\\ & =\underset{C}{\mathrm{argmin}}L(y,C)\end{array}$$

其中$y_i$为真实标签，$C$为任意常数。以上式子表示，找出令${\sum }_{i=1}^{M}l(y_i,C)$最小的常数$C$值，并输出最小的${\sum }_{i=1}^{M}l(y_i,C)$作为$H_0(x)$的值。需要注意的是，由于$H_0(x)$是由全部样本的$l$计算出来的，因此所有样本的初始值都是$H_0(x)$，不存在针对某一样本的单一初始值。

开始循环，for t in 1,2,3…T:

2. 在现有数据集$N$中，抽样$M$ * subsample个样本，构成训练集$N^t$
   
   
3. 对任意一个样本$i$，计算伪残差（pseudo-residuals）$r_{it}$，具体公式为：
   
   $$r_{it}=-\frac{\partial l(y_i,H_{t-1}(x_i))}{\partial H_{t-1}(x_i)}$$
   不难发现，伪残差是一个样本的损失函数对该样本在集成算法上的预测值求导后取负的结果，并且在进行第t次迭代、计算第t个伪残差时，我们使用的前t-1次迭代后输出的集成算法结果。在t=1时，所有伪残差计算中的$H_{t-1}(x_i)$都等于初始$H_0(x)$，在t>0时，每个样本上的$H_{t-1}(x_i)$都是不同的取值。
   
   
4. 求解出伪残差后，在数据集$(x_i,r_{it})$上按照CART树规则建立一棵回归树$f_t$，训练时拟合的标签为样本的伪残差$r_{it}$。
   
   
5. 将数据集$N_t$上所有的样本输入$f_t$进行预测，对每一个样本，得出预测结果$f_t(x_i)$。在数学上我们可以证明，只要拟合对象是伪残差$r_{it}$，则$f_t(x_i)$的值一定能让损失函数最快减小。
   
   
6. 根据预测结果$f_t(x_i)$迭代模型，具体来说：
   $$H_t(x_i)=H_{t-1}(x_i)+f_t(x_i)$$
   假设输入的步长为$\eta$，则$H_t(x)$应该为：
   $$H_t(x_i)=H_{t-1}(x_i)+\eta f_t(x_i)$$
   对整个算法则有：
   $$H_t(x)=H_{t-1}(x)+\eta f_t(x)$$

7. 循环结束，输出$H_T(x)$的值作为集成模型的输出值。

以上就是GBDT完整的数学流程，不难发现，这个流程是比AdaBoost的流程更简洁的。当然，整体流程当中可能有不少令人困惑的地方，我们来一一解明：

2 初始化$H_0$过程中的常数C是什么？

在最初的论文中，Friedman定义了如下公式来计算$H_0$：

$$H_0(x)=\underset{C}{\mathrm{argmin}}\sum _{i=1}^{M}l\left(y_i,C\right)$$$$=\underset{C}{\mathrm{argmin}}L\left(y_i,C\right)$$

其中$y_i$为真实标签，$C$为任意常数。以上式子表示，找出令整体损失$L(y_i,C)$最小的常数$C$值，并输出最小的$L(y_i,C)$作为$H_0(x)$的值。在刚观察这个式子时，大家可能很难理解$C$这个常数的作用，但这个式子实际上很简单——

首先，$l$是损失函数，损失函数衡量两个自变量之间的差异，因此$l(y_i,C)$衡量样本$i$的真实标签$y_i$与常数C之间的差异，因此$L(y_i,C)$是所有样本的真实标签与常数C之间的差异之和。现在我们要找到一个常数C，令所有样本的真实标签与常数C的差异之和最小，请问常数C是多少呢？这是一个典型的求极值问题，只需要对${\sum }_{i=1}^{M}l(y_i,C)$求导，再令导数为0就可以解出令${\sum }_{i=1}^{M}l(y_i,C)$最佳的C。假设$l$是squared_error，每个样本的平方误差，则有：

$$\sum _{i=1}^{M}l(y_i,C)=\sum _{i=1}^M(y_i-C{)}^2$$

对上述式子求导，并令一阶导数等于0：

$$\begin{array}{rl}\frac{\partial }{\partial C}\sum _{i=1}^{M}l\left(y_i,C\right)& =\frac{\partial }{\partial C}\sum _{i=1}^M{\left(y_i-C\right)}^2\\ & =\sum _{i=1}^M-2\left(y_i-C\right)\\ & =-2\sum _{i=1}^M{y}_i+2MC\\ & =0\end{array}$$
所以：
$$\begin{array}{rl}2\sum _{i=1}^M{y}_i& =2MC\\ C& =\frac{1}{M}\sum _{i=1}^M{y}_i\\ C& =\mathrm{mean}\left(y_i\right)\end{array}$$

可知，当L是平方误差squared error时，令$L(y_i,C)$最小的常数C就是真实标签的均值，这个过程与我们在学习Kmeans时证明各点到质心（均值）的距离就是最小SSE完全一致。因此，式子$H_0={\mathrm{argmin}}_C{\sum }_{i=1}^{M}l(y_i,C)$的本质其实是求解$C=mean(y_i)$时的损失函数，并以此损失函数作为$H_0$的值。当然，如果我们选择了其他的损失函数，我们就需要以其他方式（甚至梯度下降）进行求解，$C$的值可能也就不再是均值了。

3 伪残差与残差、梯度有什么关系？

在讲解GBDT与AdaBoost之间的差异时，我们曾提到，AdaBoost是拟合原始数据$X$与真实标签$y_i$，而GBDT拟合的是原始数据$X$与残差$(y_i-H(x_i))$，但在上述数学流程中，我们拟合的对象伪残差既不像真实标签，也不像$H(x)$与$y_i$的差异，它到底是什么呢？

$$r_{it}=-\frac{\partial l(y_i,H_{t-1}(x_i))}{\partial H_{t-1}(x_i)}$$

从数学上来看，伪残差是一个样本的损失函数对该样本在集成算法上的预测值求导后取负的结果。假设现在损失函数是平方误差Squared error，则该求导过程很明显就是：

$$\begin{array}{rl}l& ={\left(y_i-H_{t-1}\left(x_i\right)\right)}^2\\ \frac{\partial l}{\partial H_{t-1}\left(x_i\right)}& =\frac{\partial }{\partial H_{t-1}\left(x_i\right)}{\left(y_i-H_{t-1}\left(x_i\right)\right)}^2\\ \frac{\partial l}{\partial H_{t-1}\left(x_i\right)}& =-2\left(y_i-H_{t-1}\left(x_i\right)\right)\\ -\frac{\partial l}{\partial H_{t-1}\left(x_i\right)}& =2\left(y_i-H_{t-1}\left(x_i\right)\right)\end{array}$$

不难发现，虽然伪残差看着与残差完全不相关，但其本质与残差非常相似。它是残差的某种变形，它的值不完全等同于残差的值，但是它衡量的差异与残差衡量的差异完全一致。因此，我可以让新建立的弱评估器拟合伪残差，这样算法就会更多地学习当下$H_t(x_i)$与$y_i$之间的差异，新建立的弱评估器预测出的结果也更有可能抹平这种差异。从直觉上来说，$H_t(x_i)$与$y_i$之间的差异越小，整体损失函数值就会越小，因此GBDT拟合伪残差是在向着损失函数最小化（偏差最小化）的方向拟合。

除此之外，伪残差是损失函数求导后取负的结果。一个函数对自变量求导后得到的结果称为梯度，代表字母为$g$，因此伪残差也被称为负梯度，也因此，GBDT被称为“拟合负梯度”的算法。这一说法拓展开来，我们可以说GBDT拟合负梯度、拟合伪残差、拟合损失函数在预测标签上的负导数。无论这些说法如何变化，其实指的都是同一个数学过程。不过，在最初的梯度提升机器（Gradient Boosting Machine）中，拟合的的确是残差$y-H(x)$，只不过在后来改进的梯度提升树中，拟合残差过程被修改为拟合伪残差了。

需要注意的是，由于伪残差/负梯度都是针对单一样本计算的，所以一般在数学公式当中，梯度会被表示为$g_i$，其中$i$为样本量。对GBDT来说则有：

$$r_i=-g_i$$

4 证明：拟合伪残差可以令损失函数最快地减小

从直觉上来看，拟合伪残差可以降低$H_t(x_i)$与$y_i$之间的差异，从而降低整体损失函数的值，但这个行为在数学上真的可行吗？毕竟，GBDT可以使用任意可微函数作为损失函数，不同损失函数求导后的结果即便与残差相似，也未必能代替真正的残差的效果。因此，不仅在直觉上需要理解拟合伪残差的作用，我们还需要从数学上证明：只要拟合对象是伪残差$r_{it}$，则弱评估器的输出值$f_t(x_i)$一定是让损失函数减小最快的值。

• 直观类比

假设现在有包含$M$个样本的数据集$N^t$，无论我们以什么规则建立新的弱评估器$f_t$，我们一定是希望$f_t$满足以下条件的：

$$\begin{array}{rl}{f}_t& =\underset{f}{\mathrm{argmin}}L\left(y_i,H_t(x)\right)\\ & =\underset{f}{\mathrm{argmin}}\sum _{i=1}^{M}l\left(y_i,H_{t-1}\left(x_i\right)+f_t\left(x_i\right)\right)\end{array}$$

上式表示，本轮弱评估器的输出值$f_t$应该是令整体损失$L$最小化的$f_t$。即，无论弱评估器$f_t$是什么结构、什么规则、如何建立、如何拟合，其最终的输出值$f_t(x_i)$必须是令整体损失函数$L$最小化的$f_t(x_i)$。如果我们能保证这个条件成立，那随着算法逐步迭代，损失函数必然是会越来越小的。那我们如何保证这一点成立呢？在这里，我们需要使用论文《梯度下降式提升算法》中所提到的函数式梯度下降了——我们可以直接对整体损失函数进行梯度下降，找出当前最小值以及最小值对应的$f_t(x_i)$。

具体来说，回忆我们在逻辑回归中执行的梯度下降过程，当时我们的损失函数为$L(\mathbf{w})$，其中$w$是逻辑回归的系数向量，且迭代$w$的方法如下：

$$w_t=w_{t-1}-\eta g_t$$

公式中$\eta$为学习率，$g_t$为第$t$次迭代中的梯度向量，包含了全部$w$的梯度$[g_1,g_2,g_3...g_n]$。通过在$w$上直接增加学习率*负梯度，我们可以保证损失函数$L(\mathbf{w})$在$w$迭代过程中一定是越来越小的，因为在学习梯度下降时我们证明过，负梯度的方向就是损失函数下降最快的方向。那相同的思路也可以被用到GBDT当中。

在GBDT中，我们的损失函数为$L(y_i,H_t(x))$，并且我们的$H_t(x)$是按以下方式迭代的：

$$H_t(x)=H_{t-1}(x)+\eta f_t(x)$$

其中$H_t(x)$是，第$t$次迭代中全部样本在算法上的输出值，$f_t(x)$则是第$t$次迭代中全部样本在新弱评估器上输出的$f_t(x_i)$。原则上来说，对标传统梯度下降，只要让$f_t(x)=-g_t$，即让$f_t(x_i)=-g_i$，就一定能够保证损失函数$L(y_i,H_t(x))$是随迭代下降的。

当我们已经知道能够令损失函数最小的$f_t(x_i)$就是$-g_i$之后，如何逼迫新建立的弱评估器输出$-g_i$这个数字呢？答案是，让新建立的弱评估器拟合($x_i$,$-g_i$)。所以你现在应该已经猜到了，每个样本的伪残差$r_i$（负梯度$-g_i$）其实就是能够令损失函数减小最快的$f_t(x_i)$的值。

• 严谨证明

当然，上述过程只是类比，并非严谨的数学证明。如果我们想要证明负梯度就是让损失函数减小最快的值，则需要借助泰勒级数来帮助我们。

在数学中，泰勒级数使用无限个项的连加式来表示一个函数。实际应用当中，我们一般取有限项的连加式来逼近一个函数。当总共有N项时，连加式被叫做N阶泰勒展开（Nth-order Taylor approximation）。假设现在存在函数$f(x)$，则有：

• 泰勒级数（无限项）：
  $$f(x)=\sum _{n=0}^{\infty }\frac{f^{(n)}(a)}{n!}(x-a{)}^n$$

其中(x-a)是非常小的任意实数/复数，$n!$是n的阶乘，$f^{(n)}(a)$是函数$f(x)$的n阶导数在a点的取值。当a为0时，泰勒级数也被叫做麦克劳思级数。

• 一阶泰勒展开：
  $$\begin{array}{rl}f(x)& \approx \sum _{n=0}^1\frac{f^{(n)}a}{n!}(x-a{)}^n\\ & \approx f(a)+\frac{f^{\prime }(a)}{1!}(x-a)\end{array}$$

• 二阶泰勒展开：
  $$\begin{array}{rl}f(x)& \approx \sum _{n=0}^2\frac{f^{(n)}a}{n!}(x-a{)}^n\\ & \approx f(a)+\frac{f^{\prime }(a)}{1!}(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2\end{array}$$

• N阶泰勒展开：
  $$\begin{array}{rl}f(x)& \approx \sum _{n=0}^N\frac{f^{(n)}a}{n!}(x-a{)}^n\\ & \approx f(a)+\frac{f^{\prime }(a)}{1!}(x-a)+\frac{f^{\prime \prime }(a)}{2!}(x-a{)}^2+\frac{f^{\prime \prime \prime }(a)}{3!}(x-a{)}^3+...\end{array}$$

阶数越大，泰勒展开的值越接近$f(x)$的真实值。
我们可以对损失函数进行泰勒展开。对单一样本而言，我们有损失函数$l(y_i,H_{t-1}(x_i)+f_t(x_i))$，其中$y_i$是已知的常数，因此损失函数可以被看做是只有$H_{t-1}(x_i)+f_t(x_i)$一个自变量的函数，从而简写为$l(H_{t-1}(x_i)+f_t(x_i))$。

根据一阶泰勒展开，已知：

$$\begin{array}{rl}f(x)& \approx f(a)+\frac{f^{\prime }(a)}{1!}(x-a)\\ & \approx f(a)+f^{\prime }(a)(x-a)\end{array}$$

令泰勒展开中的 x = $H_{t-1}(x_i)+f_t(x_i)$，令泰勒展开中的a = $H_{t-1}(x_i)$，则损失函数$l(H_{t-1}(x_i)+f_t(x_i))$可以被表示为：

$$\begin{array}{rl}l(H_{t-1}(x_i)+f_t(x_i))& \approx l(H_{t-1}(x_i))+\frac{\partial l(H_{t-1}(x_i))}{\partial H_{t-1}(x_i)}\ast f_t(x_i)\end{array}$$
不难发现，该式子中$H_{t-1}(x_i)$是常数，因此第一部分$l(y_i,H_{t-1}(x_i))$也是一个常数。同时，第二部分由导数和$f_t$组成，其中导数就是梯度，可以写作$g_i$，所以式子可以化简为：
$$\begin{array}{rl}l(H_{t-1}(x_i)+f_t(x_i))& \approx 常数+g_i{f}_t(x_i)\end{array}$$

现在，如果要令$l$最小，$f_t(x_i)$应该等于多少呢？回到我们最初的目标，找出令损失函数$l$最小的$f_t$值：

$$\begin{array}{rl}{f}_t& =\underset{f}{\mathrm{argmin}}\sum _{i=1}^{M}l\left(H_{t-1}\left(x_i\right)+f_t\left(x_i\right)\right)\\ & \approx \underset{f}{\mathrm{argmin}}\sum _{i=1}^M\left(\text{ 常数 }+g_i{f}_t\left(x_i\right)\right)\end{array}$$

常数无法被最小化，因此继续化简：
$$\begin{array}{rl}{f}_t& \approx \underset{f}{\mathrm{argmin}}\sum _{i=1}^M{g}_i{f}_t\left(x_i\right)\\ & \approx \underset{f}{\mathrm{argmin}}⟨g_t{f}_t(x)⟩\end{array}$$

现在，$g_t$是包含了所有样本梯度的向量，$f_t(x)$是包含了所有样本在$f_t$上预测值的向量，两个向量对应位置元素相乘后求和，即表示为向量的内积，由尖括号<>表示。现在我们希望求解向量内积的最小值、并找出令向量内积最小的$f_t(x)$的取值，那就必须先找出$f_t(x)$的方向，再找出$f_t(x)$的大小。

[g1f(x1) + g2f(x2) + g3(fx3)...gM(fxM)]

[g1,g2,g3....gM] - 梯度向量
[f(x1),f(x2),f(x3)....f(xM)] - ft决策树上输出的所有样本的预测值

• 方向

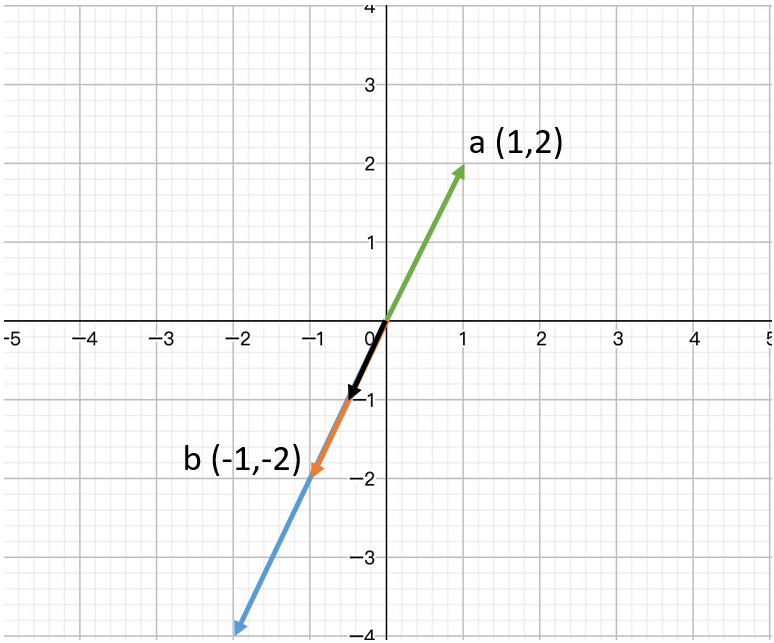
$f_t(x)$的方向应该与$g_t$完全相反。向量的内积$⟨g_t{f}_t(x)⟩=|g_t||f_t(x)|cos(\alpha )$，其中前两项为两个向量的模长，$\alpha$是两个向量的夹角大小。模长默认为整数，因此当且仅当两个向量的方向完全相反，即夹角大小为180度时，$cos(\alpha )$的值为-1，才能保证两个向量的内积最小。假设向量 a = [1,2]，向量b是与a的方向完全相反的向量。假设a和b等长，那向量b就是[-1,-2]。因此，与$g_t$方向完全相反且等长的向量就是$-g_t$，$f_t(x)$的方向也正是$-g_t$的方向。

• 大小

对于向量a，除了[-1,-2]之外，还存在众多与其呈180度夹角、但大小不一致的向量，比如[-2,-4], [-0.5,-1]，每一个都可以与向量a求得内积。并且我们会发现，当方向相反时，向量b中的元素绝对值越大，b的模长就越长，向量a与b的内积就越小。因此不难发现，$⟨g_t{f}_t(x)⟩$是一个理论上可以取到无穷小的值，那我们的$f_t(x)$应该取什么大小呢？答案非常出乎意料：任何大小都无所谓。

回到我们的迭代公式：
$$H_t(x)=H_{t-1}(x)+\eta f_t(x)$$$$l(H_{t-1}(x_i)+f_t(x_i))\approx 常数+g_i{f}_t(x_i)$$

无论$f_t(x)$的大小是多少，我们都可以通过步长$\eta$对其进行调整，只要能够影响$H_{(}x)$，我们就可以影响损失迭代过程中的常数的大小。因此在数学上来说，$f_t(x)$的大小可以是$-g_t$的任意倍数，这一点在梯度下降中其实也是一样的。为了方便起见，同时为了与传统梯度下降过程一致，我们通常让$f_t(x)$就等于一倍的$-g_t$，但也有不少论文令$f_t(x)$等于其他值的。在GBDT当中：
$$\begin{array}{rl}{f}_t& \approx {\mathrm{argmin}}_f⟨g_t{f}_t(x)⟩\\ & =-g_t\end{array}$$
这就是我们让GBDT当中的弱评估器拟合伪残差/负梯度的根本原因。拟合负梯度其实为GBDT带来了非常多的特点——

1. 首先，通过直接拟合负梯度，GBDT避免了从损失函数找“最优”的过程，即避免了上述证明中求解$f_t={\mathrm{argmin}}_f{\sum }_{i=1}^{M}l(H_{t-1}(x_i)+f_t(x_i))$的过程，从而大大地简化了计算。

2. 其次，通过拟合负梯度，GBDT模拟了梯度下降的过程，由于结合了传统提升法Boosting与梯度下降，因此才被命名为梯度提升法（Gradient Boosting）。这个过程后来被称为函数空间上的梯度下降（Gradient Descent in Function Space），这是视角为Boosting算法的发展奠定了重要的基础。

3. 最后，最重要的一点是，通过让弱评估器拟合负梯度，弱评估器上的结果可以直接影响损失函数、保证损失函数的降低，从而指向Boosting算法的根本目标：降低偏差。这一过程避免了许多在其他算法中需要详细讨论的问题：例如，每个弱评估器的权重$\varphi$是多少，以及弱评估器的置信度如何。

在AdaBoost算法当中，损失函数是“间接”影响弱评估器的建立，因此有的弱评估器能够降低损失函数，而有的弱评估器不能降低损失函数，因此要在求和之前，需要先求解弱评估器的置信度，然后再给与置信度高的评估器更高的权重，权重$\varphi$存在的根本意义是为了调节单一弱评估器对$H(x)$的贡献程度。但在GBDT当中，由于所有的弱评估器都是能够降低损失函数的，只不过降低的程度不同，因此就不再需要置信度/贡献度的衡量，因此就不再需要权重$\varphi$。

如果去翻阅早期梯度提升机器资料，我们会发现梯度提升树最开始是有求解权重的过程的。当拟合完伪残差之后，我们不直接求解令$L$最小的$f_t$值，而求解令整体$L$最小的权重$\varphi$：

求解迭代过程中弱评估器$f_t$所需的权重${\varphi }_t$，具体公式为：

$${\varphi }_t={\mathrm{argmin}}_{\varphi }\sum _{i=1}^{M}L\left(y_i,H_{t-1}(x_i)+{\varphi }_t{f}_t(x_i)\right)$$
与求解$H_0$的式子相似，上述式子表示，找出令${\sum }_{i=1}^{M}L\left(y_i,H_{t-1}(x_i)+{\varphi }_t{f}_t(x_i)\right)$最小的常数${\varphi }_t$值。同样，由于${\varphi }_t$是针对全部样本计算出来的，因此$f_t$上所有样本的预测值前的权重都是${\varphi }_t$，并不存在针对于某一样本的权重。


接着，再根据求解出的权重${\varphi }_t$迭代模型，具体来说：

$$H_t(x)=H_{t-1}(x)+\eta {\varphi }_t{f}_t(x)$$

在此基础上，Friedman甚至还提出了单独针对决策树的权重计算方法。但我们之前推导中讲解过，只要$f_t(x)$的方向正确，$f_t(x)$具体的取值并没有那么重要，毕竟可以通过学习率$\eta$进行调整。在有$\eta$、同时又不需要衡量弱评估器置信度的情况下，权重$\varphi$的意义就很小了。因此现在我们在实现梯度提升树时，已经不再使用带权重的版本，但带权重版本的数学过程与不带权重版本是高度类似的。

讲到这里，梯度提升树相关的知识也就讲解完毕了。在课程当中我们专注于GBDT回归的讲解，是因为GBDT分类问题就是在回归问题的流程上令$p(x)=\sigma (H(x))$，其中$\sigma$依情况而定可能是softmax也可能是sigmoid或其他函数。如果你对GBDT分类感兴趣，可以阅读原理进阶部分提到的4篇论文，里面有大量关于分类问题的讲解。现在，我们已经了解了整个GBDT的数学流程，这部分流程是未来XGBoost、LGBM等算法的基础。如果你对Boosting算法的数学理论有相应的需求，请务必熟读GBDT原理相关的内容。