入门-动态规划

1. 分梨

题目描述
小明非常喜欢吃梨，有一天他得到了ACMCLUB送给他的一筐梨子。由于他比较仗义，就打算把梨子分给好朋友们吃。现在他要把M个梨子放到N个盘子里面（我们允许有的盘子为空），你能告诉小明有多少种分法吗？（请注意，例如有三个盘子，我们将5,1,1和1,1,5，视为同一种分法）

输入
输入包含多组测试样例。每组输入的第一行是一个整数t。
接下来t行，每行输入两个整数M和N，代表有M个梨和N个盘子。（M和N均大于等于0）

输出
对于每对输入的M和N，输出有多少种方法。

样例输入

1
7 3

样例输出

8

解析 递归分配

M个梨， N个盘子的分法
dp(m, n){
	if (只有一个盘子 || 没有梨)
		只有一种分法；
	if (盘子N比梨M多)
		则最多用M个盘子, dp(m,n) = dp(m,m)；
	else 
		如果每个至少一个梨， 则dp(m-n, n)
		如果有一个盘子为空， 则dp(m, n-1)
		dp(m, n) = dp(m, n-1) + dp(m-n, n)

}

AC

#include<stdio.h>
int c(int x,int y)
{       
	if(y == 1 || x == 0)
        	return 1;
	if(x<y)      
    		return c(x,x);
	else
    		return c(x,y-1)+c(x-y,y);               
}

int main()
{
	int t,n,m;
 
    while(scanf("%d",&t)!=EOF)
    {
    	while(t--)
        {
        	scanf("%d%d",&m,&n);
            printf("%d\n",c(m,n));
        }
    }       
    return 0;
}

2. 最大公共子序列

见之前的博客

3. 最大子段和

Problem Description
Given a sequence a[1],a[2],a[3]…a[n], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14.

Input
The first line of the input contains an integer T(1<=T<=20) which means the number of test cases. Then T lines follow, each line starts with a number N(1<=N<=100000), then N integers followed(all the integers are between -1000 and 1000).

Output
For each test case, you should output two lines. The first line is “Case #:”, # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence, the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases.

Sample Input

2
5 6 -1 5 4 -7
7 0 6 -1 1 -6 7 -5

Sample Output

Case 1:
14 1 4

Case 2:
7 1 6

解析

sum, maxsum = M[n-1]
for auto m : M[]:
	sum = max(sum+m, m)
	if sum >= maxsum:
		maxsum = sum

AC

#include <iostream>
#include <cstring>

using namespace std;

int M[100005], arr[100005];
int l, r;
int maxSubArr(int D[], int n){
	int i, sum = 0, maxsum = D[n-1];
	l = n-1;
	for (i=n-1; i>=0; i--){
		if (sum > 0){
			sum = sum + D[i];
		}else{
			sum = D[i];
		}
		if (sum >= maxsum) { //If there are more than one result, output the first one.
			maxsum = sum;
			l = i;
		}
	}
	return maxsum;
}

int main(){
 	int T, N;
 	cin>>T;
 	for (int t=1; t<=T; t++){
 		cin>>N;
 		for (int i=0; i<N; i++){
 			cin>>M[i];
		}
		int ans = maxSubArr(M, N);
		cout<<"Case "<<t<<":"<<endl;
		int s = 0;
		for (int i = l; i<N; i++){
			s += M[i];
			if (s == ans){
				r=i;
				break;
			}
		}
		cout<<ans<<" "<<l+1<<" "<<r+1<<endl;
		if (t<T){
			cout<<endl;
		}
	}
 	return 0;
 } 

4. 最大子阵和

Problem Description
Given a two-dimensional array of positive and negative integers, a sub-rectangle is any contiguous sub-array of size 1 x 1 or greater located within the whole array. The sum of a rectangle is the sum of all the elements in that rectangle. In this problem the sub-rectangle with the largest sum is referred to as the maximal sub-rectangle.

As an example, the maximal sub-rectangle of the array:

0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

is in the lower left corner:

9 2
-4 1
-1 8

and has a sum of 15.

Input
The input consists of an N x N array of integers. The input begins with a single positive integer N on a line by itself, indicating the size of the square two-dimensional array. This is followed by N 2 integers separated by whitespace (spaces and newlines). These are the N 2 integers of the array, presented in row-major order. That is, all numbers in the first row, left to right, then all numbers in the second row, left to right, etc. N may be as large as 100. The numbers in the array will be in the range [-127,127].

Output
Output the sum of the maximal sub-rectangle.

Sample Input

4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

Sample Output

15

解析

这一题可以借助上一题的思路，把求最大子阵转化为求最大子段和，也就是变成一维情况。
(以第一行最为开始)先求第一行的最大和;将第二行数据加到第一行，再求此时的最大值;再将下一行加上去，求最大值.....;
.最终得到第一列到最后一列的最大值；还要计算第二行到最后一行的最大和，第三行到最后一行的最大和；

fun(){
//求最大子段和
}

for i = 0 : N #第i行到j行最大子阵和
	# 第一次循环结束，我们得到的是第一行到第N行的N x M的最大子阵和（N是行数，M是列数，M由fun（）决定）
	# 第二次循环结束，我们得到的是第二行到第N行的N-1 x M的最大子阵和
	for j = i : N 
		把第j行加到array上：arry[k] = M[j][k]
		计算array的最大子段和：fun(array)
	
		
	

AC

#include <iostream>
#include <cstring>

using namespace std;

int M[105][105], arr[105];
int maxSubArr(int D[], int n){
	int sum=0, maxsum=D[0];
	for (int i=0; i<n; i++){
		if (sum>0){
			sum = sum + D[i];
		}else{
			sum = D[i];
		}
		if (sum > maxsum) maxsum = sum;
	}
	return maxsum;
}

int main(){
 	int N;
 	while(scanf("%d", &N) != EOF){//注意输入
 		for (int i=0; i<N; i++){
	 		for (int j=0; j<N; j++){
	 			cin>>M[i][j];
			}
		}
		int maxsubrec = M[0][0];
		for (int i=0; i<N; i++){
			memset(arr, 0, sizeof(arr));
			for (int j=i; j<N; j++){
				for (int k=0; k<N; k++){
					arr[k] += M[j][k];
				}
				int maxsubarr = maxSubArr(arr, N);
				if (maxsubarr > maxsubrec) maxsubrec = maxsubarr;
			} 
		}
		cout<<maxsubrec<<endl;
	}
 	return 0;
 } 

5. 母牛的故事

Problem Description
有一头母牛，它每年年初生一头小母牛。每头小母牛从第四个年头开始，每年年初也生一头小母牛。请编程实现在第n年的时候，共有多少头母牛？

Input
输入数据由多个测试实例组成，每个测试实例占一行，包括一个整数n(0<n<55)，n的含义如题目中描述。
n=0表示输入数据的结束，不做处理。

Output
对于每个测试实例，输出在第n年的时候母牛的数量。
每个输出占一行。

Sample Input

2
4
5
0

Sample Output

2
4
6

解析

 f(n) = f(n-1) + f(n-3)

AC

#include<stdio.h>
//递归 
 int sum(int n)
{
    if (n <= 4) return n;
    else return (sum(n-1) + sum(n - 3));
}
int main()
{
    int n;
    while (~scanf("%d", &n) != EOF&&n!=0)
        printf("%d\n", sum(n));
    getchar();
    return 0;
}

6. 数塔

Problem Description
在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

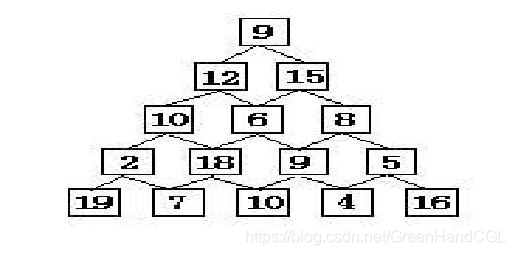
已经告诉你了，这是个DP的题目，你能AC吗?

Input
输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

Output
对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。

Sample Input

1
5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

Sample Output

30

解析

递推公式：DP[i][j] = M[i][j] + max(DP[i+1][j], DP[i+1][j+1])
自底向上计算到塔顶，得到的结果即为最大和

AC

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

int main()
{
    int a[105][105];
    int t, n, i, j;
    while(cin>>t)
    {
        while(t--)
        {
            cin>>n;
            memset(a,0,sizeof(a));
            for(i=0; i<n; i++)
                for(j=0; j<=i; j++)
                    cin>>a[i][j];
            for(i=n-2; i>=0; i--)
                for(j=0; j<=i; j++)
                    a[i][j] = a[i][j] + max(a[i+1][j], a[i+1][j+1]);
            cout<<a[0][0]<<endl;
        }
    }
    return 0;
}

7. 一只小蜜蜂

Problem Description
有一只经过训练的蜜蜂只能爬向右侧相邻的蜂房，不能反向爬行。请编程计算蜜蜂从蜂房a爬到蜂房b的可能路线数。
其中，蜂房的结构如下所示。

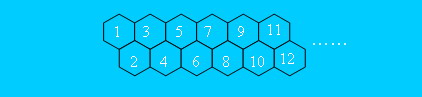
Input
输入数据的第一行是一个整数N,表示测试实例的个数，然后是N 行数据，每行包含两个整数a和b(0<a<b<50)。

Output
对于每个测试实例，请输出蜜蜂从蜂房a爬到蜂房b的可能路线数，每个实例的输出占一行。

Sample Input

2
1 2
3 6

Sample Output

1
3

解析

思路1：局部最优解得到全局最优解
蜂房5路线 = 蜂房3的路线 + 蜂房4的路线
蜂房6路线 = 蜂房4的路线 + 蜂房5的路线
。。。
蜂房n路线 = 蜂房n-2的路线 + 蜂房n-1的路线
斐波那契数列

思路2：枚举
1->2 (1种)：1->2;
1->3 (2种): 1->2->3; 1->3;
1->4 (3种): 1->2->4; 1->2->3->4; 1->3->4;
1->5 (5种): 1->2->3->5; 1->3->5; 1->2->4->5; 1->2->3->4->5; 1->3->4->5;
1->6 (8种): 1->4(3种)->6; 1->5(5种)->6;
得斐波那契数列

唯一要注意的就是数比较大，得用long long类型

AC

#include <iostream>
using namespace std;

int main()
{
	long long ans = 0, pre = 0;
	int T;
	cin>>T;
	while(T--){
		int a, b;
		cin>>a>>b;
		for (int i=2; i <= b-a+1; i++){
			if (i==2) {
				pre = 0;
				ans = 1;
			}
			else if (i==3) {
				pre = 1;
				ans = 2; continue;
			}else{
				ans = pre + ans;
				pre = ans - pre;
			}
		}
		cout << ans << endl;
	} 
	return 0; 
}

8. 折线分割平面

Problem Description
我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。

Input
输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。

Output
对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

Sample Input

2
1
2

Sample Output

2
7

解析

n条直线最多分平面问题
题目大致如:n条直线，最多可以把平面分为多少个区域。
析:可能你以前就见过这题目，这充其量是一道初中的思考题。但一个类型的题目还是从简单的入手，才容易发现规律。
当有n-1条直线时，平面最多被分成了f（n-1）个区域。
则第n条直线要是切成的区域数最多，就必须与每条直线相交且不能有同一交点。 
这样就会得到n-1个交点。
这些交点将第n条直线分为2条射线和n-2条线段。
而每条射线和线断将已有的区域一分为二。这样就多出了2+（n-2）个区域。
故：f(n)=f(n-1)+n
=f(n-2)+(n-1)+n
……
=f(1)+1+2+……+n
=n(n+1)/2+1

根据直线分平面可知，由交点决定了射线和线段的条数，进而决定了新增的区域数。
当n-1条折线时，区域数为f（n-1）。
为了使增加的区域最多，则折线的两边的线段要和n-1条折线的边，即2*（n-1）条线段相交。
那么新增的线段数为4*（n-1），射线数为2。
但要注意的是，折线本身相邻的两线段只能增加一个区域。
故：f(n)=f(n-1)+4(n-1)+2-1
=f(n-1)+4(n-1)+1
=f(n-2)+4(n-2)+4(n-1)+2
……
=f(1)+4+4*2+……+4(n-1)+(n-1)
=2n^2-n+1

AC

#include<iostream>
using namespace std;
 
int main()
{
	int num,k;
	cin>>num;
	while(num--)
	{
		cin>>k;
		cout<<2*k*k-k+1<<endl;
	}
	return 0;
}

9. 献给杭电五十周年校庆的礼物

Problem Description
今年是我们杭电建校五十周年，这是一个值得祝福的日子。我们该送给母校一个怎样的礼物呢？对于目前的大家来说，最好的礼物当然是省赛中的好成绩，我不能参赛，就送给学校一个DOOM III球形大蛋糕吧，这可是名牌，估计要花掉我半年的银子呢。

想象着正式校庆那一天，校长亲自操刀，把这个大蛋糕分给各地赶来祝贺的校友们，大家一定很高兴，呵呵，流口水了吧…

等一等，吃蛋糕之前先考大家一个问题：如果校长大人在蛋糕上切了N刀（校长刀法极好，每一刀都是一个绝对的平面），最多可以把这个球形蛋糕切成几块呢？

做不出这个题目，没有蛋糕吃的！
为-了-母-校-，为-了-蛋-糕-（不是为了DGMM，枫之羽最会浮想联翩…），加-油-！

Input
输入数据包含多个测试实例，每个实例占一行，每行包含一个整数n(1<=n<=1000)，表示切的刀数。

Output
对于每组输入数据，请输出对应的蛋糕块数，每个测试实例输出一行。

Sample Input

1
2
3

Sample Output

2
4
8

解析

平面分割空间问题
由二维的分割问题可知，平面分割与线之间的交点有关，即交点决定射线和线段的条数，从而决定新增的区域数。
试想在三维中则是否与平面的交线有关呢？
当有n-1个平面时，分割的空间数为f(n-1)。
要有最多的空间数，则第n个平面需与前n-1个平面相交，且不能有共同的交线。即最多有n-1 条交线。
而这n-1条交线把第n个平面最多分割成g(n-1)个区域。
（g(n)为（1）中的直线分平面的个数 ）此平面将原有的空间一分为二，则最多增加g(n-1)个空间。
故：f=f(n-1)+g(n-1) ps:g(n)=n(n+1)/2+1
=f(n-2)+g(n-2)+g(n-1)
……
=f(1)+g(1)+g(2)+……+g(n-1)
=2+(1*2+2*3+3*4+……+(n-1)n)/2+（n-1）
=(1+2^2+3^2+4^2+……+n^2-1-2-3-……-n )/2+n+1
=(n^3+5n)/6+1

AC

#include <stdio.h>

int main(){
	int n;
	while(scanf("%d", &n)!=EOF){
		printf("%d\n", (n*n*n+5*n)/6+1);
	}
	return 0;
}