L3-032 关于深度优先搜索和逆序对的题应该不会很难吧这件事（思维，树状数组）

题目链接

题意

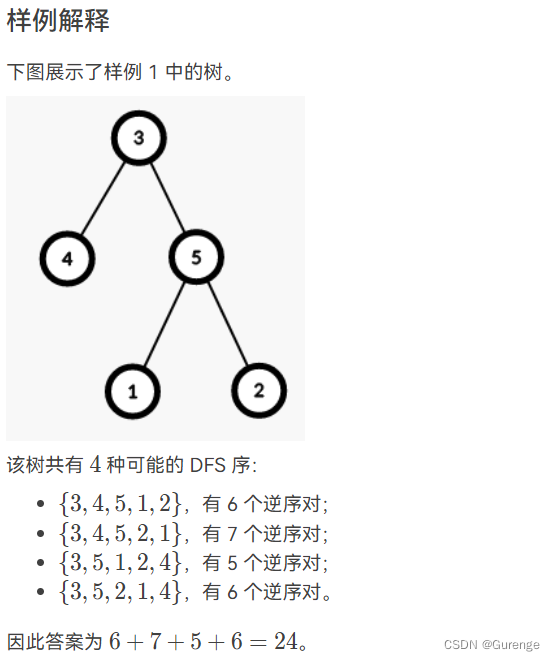
思路

    一时间无从下手，听了dls的讲解才有了写思路；

    观察到若两个点 x，y 是有祖先关系，设 x 为 y 的祖先，则无论以什么方式遍历，x 始终在 y 的前面，我们将这样的点对记为第一类点；其余没有祖先关系的点对记为第二类点；

    对与第一类点，可通过计算它与它祖先形成的逆序对，暴力枚举祖先肯定会超时，在普通逆序对计算时，我们可以通过树状数组 / 线段树等数据结构快速地得到一个点的逆序对个数，所以如果对于一个点 x，我们将其所有祖先存在树状数组中，就可以快速得到有多少个值比它大的祖先，即逆序对个数；

    但对于每一个点，其祖先并不相同，需在树状数组中更新祖先信息，考虑对树的遍历，是不是就像维护了一个栈，当遍历到一个点就把这个点压如栈顶，遍历完这个点的子树信息之后，就把这个点弹出，我们并没有真的去维护这个栈，在 dfs 过程中，系统就帮我们维护了，其实，在遍历任一状态，这个栈当中的元素仅有当前点以及其各个祖先，故可以在遍历的过程中实现对树状数组的操作，当前点入栈时，就将其值放入树状数组，出栈时，就把其值从树状数组删去，本次天梯赛L2-043 龙龙送外卖，也用到了这个方法；

    这样就可以得到第一类点所形成的逆序对个数，还需要乘上不同遍历方式的总个数，才是第一类点的总价值；若一个点有三个儿子，在不同的遍历方式下，这三个儿子可以任意排列；树的总遍历方式即为每个点的儿子的排列方式的乘积，设第 i 个点有  个儿子，则树的总遍历方式数为 ；

   下面分析第二类点，若一个点有若干棵子树，则在不同遍历方式下，子树的遍历顺序不同，会有全排列种情况，属于不同子树的两个点 x，y 在全排列中，有一半的情况 x 在前，另一半 y 在前，考虑期望，则在一种遍历方式下，点对 x，y 所产生的逆序对为 1/2，乘以总的遍历方式即为该点对的总贡献；

    对于一个点 x，如何快速得到与其不是祖先关系的点，可以发现若 y 是 x 的祖先，则 y 不是第二类点，同时，若 y 在 x 的子树中，y 也不是第二类点，剩下的点即为第二类点；在该题中，每一个点的编号即为其值，也就是说每个点的权值不相同，两个不同的点在某些遍历方式下一定会形成逆序对；也就是说，我们并不需要知道具体哪些点与 x 形成第二类点，只需要知道其个数，可以通过维护子树节点数，以及深度（深度即可得到有几个点是当前点的祖先）得到，故点对 x 所形成的贡献为 遍历方式个数 * 1/2 * 第二类点的个数 * 1/2，第二个 1/2 是因为，对于点对 x，y 会计算一次贡献， y，x 又会计算一次；

代码

#include <bits/stdc++.h>

using namespace std;
typedef long long ll;
const int MOD=1e9+7;

struct node{
	int to,nex;
}edge[600010];
int head[300010],cnt;
int tree[300010],n,dep[300010],siz[300010];
ll ans,son=1,er=500000004;

inline int lowbit(int x){
	return x&-x;
}

void add(int x,int k){
	for(int i=x;i<=n;i+=lowbit(i)) tree[i]+=k;
}

int find(int x){
	int ans=0;
	for(int i=x;i>0;i-=lowbit(i)) ans+=tree[i];
	return ans;
}

void addedge(int x,int y){
	edge[++cnt].to=y;
	edge[cnt].nex=head[x];
	head[x]=cnt;
}

void dfs(int p,int f){
	siz[p]=1;
	dep[p]=dep[f]+1;
	ll tmp=find(n-p+1),x=1,yy=1;
	ans=(ans+tmp)%MOD;
	add(n-p+1,1);
	for(int i=head[p];i!=-1;i=edge[i].nex){
		int y=edge[i].to;
		if(y==f) continue;
		x=x*yy%MOD; yy++;
		dfs(y,p);
		siz[p]+=siz[y];
	}
	if(x>1) son=son*x%MOD;
	add(n-p+1,-1);
}

int main()
{
	ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
	memset(head,-1,sizeof(head));
	ll root,x,y;
	cin>>n>>root;
	for(int i=1;i<n;i++){
		cin>>x>>y;
		addedge(x,y); addedge(y,x);
	}
	dfs(root,0);
	ans=ans*son%MOD;
	for(int i=1;i<=n;i++){
		x=n-dep[i]-siz[i]+1;
		ans=(ans+x*son%MOD*er%MOD*er%MOD)%MOD;
	}
	cout<<ans<<"\n";
	return 0;
}