机器学习笔记（二）：Logistic回归

一、Logistic回归概述

1. Logistic回归的思想

Logistic回归是一种分类的算法，用于分类问题。

和很多其他机器学习算法一样，逻辑回归也是从统计学中借鉴来的，尽管名字里有回归俩字儿，但它不是一个需要预测连续结果的回归算法。

与之相反，Logistic 回归是二分类任务的首选方法。它输出一个 0 到 1 之间的离散二值结果。简单来说，它的结果不是 1 就是 0。

例如癌症检测算法可看做是 Logistic 回归问题的一个简单例子，我们通过Logistic回归算法可以构造出一条决策边界，这种算法输入病理数据并且应该将患有癌症和没有癌症的数据分离开，以此预测患者是患有癌症（1）或没有癌症（0）。

(当然，Logisitc算法也可以处理多个分类问题，我们先从最简单的二分类问题开始学习)

因此，我们需要完成以下几个步骤：

• 寻找合适的假设函数，即分类函数，用以预测输入数据的判断结果；

• 构造代价函数，即损失函数，用以表示预测的输出结果与训练数据的实际类别之间的偏差；

• 最小化代价函数，从而获取最优的模型参数。

二. Logistic回归具体步骤的推导

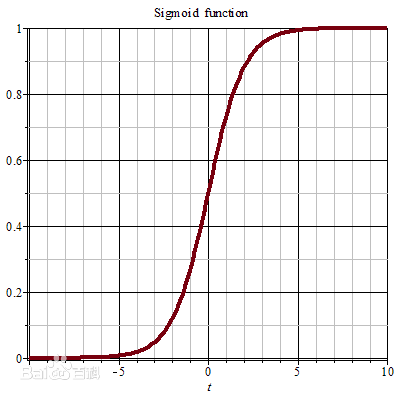
1.构造逻辑函数（sigmoid函数）

logistic回归主要是进行二分类预测，也即是对于0~1之间的概率值，当概率大于0.5预测为1，小于0.5预测为0.Sigmoid函数恰好符合我们的需求，因此选用sigmoid函数。

函数表达式为：
$$h(z)=\frac{1}{1+e^{-z}}$$
其图像为：

2.构造代价函数：

那么，为了区分数据，需要构造一条边界函数将数据分成两块。线性边界可定义为:$${\theta }_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n=\sum _{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$$

所以 $$h_{\theta }({\theta }^{T}x)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

代价函数定义为： $$J(\theta )=\frac{1}{m}\sum _{i=1}^{m}Cost(h_{\theta }(x^{(i)}),y^{(i)})$$

$$Cost(h_{\theta }(x),y)=-ylog(h_{\theta }(x))-(1-y)log(1-h_{\theta }(x))$$

代价函数的具体推导过程：

$h_{\theta }(x)$函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：
$$P(y=1|x;\theta )=h_{\theta }(x)$$
$$P(y=0|x;\theta )=1-h_{\theta }(x)$$

而$Cost$函数$J(\theta )$是通过最大似然估计推导的。下面详细说明推导过程：

由上式可以综合构造出概率函数：$$P(y|x;\theta )=(h_{\theta }(x){)}^y(1-h_{\theta }(x){)}^{1-y}$$

取似然函数为：$$L(\theta )=\prod _{i=1}^{m}P(y^{(i)}|x^{(i)};\theta )$$
$$=\prod _{i=1}^m(h_{\theta }(x^{(i)}){)}^{y^{(i)}}(1-h_{\theta }(x^{(i)}){)}^{1-y^{(i)}}$$

对数似然函数为：
$$l(\theta )=logL(\theta )$$
$$=\sum _{i=1}^m(y^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)})))$$
最大似然估计就是要使得$l(\theta )$取最大值时的$\theta$，其实这里可以使用梯度上升方法求解，求得$\theta$就是要求的最佳参数，但是，在Andrew Ng的课程中将$J(\theta )$取为：
$$J(\theta )=-\frac{1}{m}l(\theta )$$

因为乘了一个负的系数$-\frac{1}{m}$，所以$J(\theta )$取最小值时的$\theta$为要求的最佳参数

3.最小化代价函数：

最小化代价函数经常使用梯度下降来求$J(\theta )$的最小值：

$${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )(j=0\dots n)$$ ($\alpha$为学习速率)

求$J(\theta )$的偏导：
$$\frac{\partial }{\partial {\theta }_j}J(\theta )=-\frac{1}{m}\sum _{i=1}^m\left(y^{(i)}\frac{1}{h_{\theta }(x^{(i)})}\frac{\partial }{\partial {\theta }_j}{h}_{\theta }(x^{(i)})-(1-y^{(i)})\frac{1}{1-h_{\theta }(x^{(i)})}\frac{\partial }{\partial {\theta }_j}{h}_{\theta }(x^{(i)})\right)$$

$$=-\frac{1}{m}\sum _{i=1}^m\left(y^{(i)}\frac{1}{g({\theta }^T{x}^{(i)})}-(1-y^{(i)})\frac{1}{1-g({\theta }^T{x}^{(i)})}\right)\frac{\partial }{\partial {\theta }_j}g({\theta }^T{x}^{(i)})$$

$$=-\frac{1}{m}\sum _{i=1}^m\left(y^{(i)}\frac{1}{g({\theta }^T{x}^{(i)})}-(1-y^{(i)})\frac{1}{1-g({\theta }^T{x}^{(i)})}\right)g({\theta }^T{x}^{(i)})(1-g({\theta }^T{x}^{(i)}))\frac{\partial }{\partial {\theta }_j}{\theta }^T{x}^{(i)}$$

$$=-\frac{1}{m}\sum _{i=1}^m\left(y^{(i)}(1-g({\theta }^T{x}^{(x)}))-(1-y^{(i)})g({\theta }^T{x}^{(i)})\right)x_j^{(i)}$$

$$=-\frac{1}{m}\sum _{i=1}^m\left(y^i-g({\theta }^T{x}^{(i)})\right)x_j^{(i)}$$

$$=-\frac{1}{m}\sum _{i=1}^m\left(y^{(i)}-h_{\theta }(x^{(i)})\right)x_j^{(i)}$$

$$=\frac{1}{m}\sum _{i=1}^m\left(h_{\theta }(x^{(i)})-y^{(i)}\right)x_j^{(i)}$$
最后得出梯度下降的更新公式为：

$${\theta }_j:={\theta }_j-\alpha \sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)},(j=0\dots n)$$

• 优化算法：

因为梯度下降是一种迭代算法，过多的循环语句会使代码的运行时间过长，因此我们可以尽可能的利用向量代替循环语句，让代码的时间复杂度降低。

梯度下降算法的向量化解法：

训练数据的矩阵形式表示如下，其中x的每一行为一条训练样本。

$$x=\left[\begin{array}{c}{x}^{(1)}\\ x^{(2)}\\ \dots \\ x^{(m)}\end{array}\right]=\left[\begin{array}{cccc}{x}_0^{(1)}& x_1^{(1)}& \dots & x_n^{(1)}\\ x_0^{(2)}& x_1^{(2)}& \dots & x_n^{(2)}\\ \dots & \dots & \dots & \dots \\ x_0^{(m)}& x_1^{(m)}& \dots & x_n^{(m)}\end{array}\right],y=\left[\begin{array}{c}{y}^{(1)}\\ y^{(2)}\\ \dots \\ y^{(m)}\end{array}\right]$$

参数$\theta$的矩阵形式为：
$$\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ \dots \\ {\theta }_n\end{array}\right]$$
　
　　计算$X\cdot \theta$并记为A:

$$A=x\cdot \theta =\left[\begin{array}{cccc}{x}_0^{(1)}& x_1^{(1)}& \dots & x_n^{(1)}\\ x_0^{(2)}& x_1^{(2)}& \dots & x_n^{(2)}\\ \dots & \dots & \dots & \dots \\ x_0^{(m)}& x_1^{(m)}& \dots & x_n^{(m)}\end{array}\right]\cdot \left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ \dots \\ {\theta }_n\end{array}\right]=\left[\begin{array}{c}{\theta }_0{x}_0^{(1)}+{\theta }_1{x}_1^{(1)}+\cdots +{\theta }_n{x}_n^{(1)}\\ {\theta }_0{x}_0^{(2)}+{\theta }_1{x}_1^{(2)}+\cdots +{\theta }_n{x}_n^{(2)}\\ \dots \\ {\theta }_0{x}_0^{(m)}+{\theta }_1{x}_1^{(m)}+\cdots +{\theta }_n{x}_n^{(m)}\end{array}\right]$$

求$h_{\theta }(x)-y$并记为E：
$$E=h_{\theta }(x)-y=\left[\begin{array}{c}g(A^{(1)})-y^{(1)}\\ g(A^{(2)})-y^{(2)}\\ \dots \\ g(A^{(m)})-y^{(m)}\end{array}\right]=\left[\begin{array}{c}{e}^{(1)}\\ e^{(1)}\\ \dots \\ e^{(1)}\end{array}\right]=g(A)-y$$

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知$h_{\theta }(x)-y$可以由g(A)-y一次计算求得。

θ更新过程，当j=0时：
$${\theta }_0:={\theta }_0-\alpha \sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(}i))x_0^{(i)}$$

$$={\theta }_0-\alpha \sum _{i=1}^m{e}^{(i)}{x}_0^{(i)}$$

$$={\theta }_0-\alpha \cdot (x_0^{(1)},x_0^{(2)},\dots ,x_0^{(m)})\cdot E$$

θ、j同理：

$${\theta }_j:={\theta }_j-\alpha \cdot (x_j^{(1)},x_j^{(2)},\dots ,x_j^{(m)})\cdot E$$

综合起来：
$$\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ \dots \\ {\theta }_n\end{array}\right]:=\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ \dots \\ {\theta }_n\end{array}\right]-\alpha \cdot \left[\begin{array}{cccc}{x}_0^{(1)}& x_0^{(2)}& \dots & x_0^{(m)}\\ x_1^{(1)}& x_1^{(2)}& \dots & x_1^{(m)}\\ \dots & \dots & \dots & \dots \\ x_n^{(1)}& x_n^{(2)}& \dots & x_n^{(m)}\end{array}\right]\cdot E$$

$$=\theta -\alpha \cdot X^T\cdot E$$

综上所述，向量化后θ更新的步骤如下：

（1）求$A=X\cdot \theta$；

（2）求$E=g(A)-y$；

（3）求$\theta :=\theta -\alpha \cdot X^T\cdot E$

也可以综合起来写成：　$$\theta :=\theta -\alpha \cdot (\frac{1}{m})\cdot X^T\cdot (g(X\cdot \theta )-y)$$

这样就把复杂的梯度算法简化成了一行代码。

三、Python实现Logistic回归实例

Python代码：

from numpy import *
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons 
#构造数据测试集
Input_data, y = make_moons(250, noise=0.25) 
dataMat=mat(Input_data) #把输入数组转换成矩阵（之后的*就由元素对应相乘转换成了矩阵的乘法）,维度（m,n）
                        
dataLebel = mat(y).transpose() #把标签转换成矩阵,维度（m,1）
                               
dataMat=[]
n=shape(Input_data)[0]

#将x0=1,添加进输入数组中
for i in range(n):
    dataMat.append([1,Input_data[i][0],Input_data[i][1]])
    
#构造sigmoid 函数
def sigmoid (x):
    return 1/(1+exp(-x))

#构造梯度下降函数
def gradAscent(dataMat,dataLebel):
    dataMatrix=mat(dataMat)#转换成矩阵
    labelMat=mat(dataLebel)
    m,n=shape(dataMatrix) #获取输入矩阵维度（m,n）
    weights=ones((n,1)) #初始化权重矩阵，维度(n,1)
    alpha=0.001 #定义学习速率
    maxCycles=500 #学习循环次数
    for i in range(maxCycles):
        h=sigmoid(dataMatrix * weights) #sigmoid 函数
        error=labelMat - h #即y-h，（m,1）
        weights=weights + alpha * dataMatrix.transpose() * error #梯度上升法
    return weights

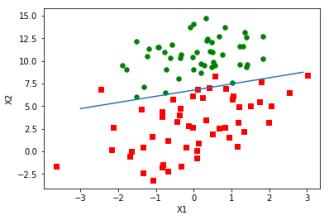
#绘制边界曲线，因为数据集有3个参数：x1,x2,y。所以将x1为横坐标，将x2为纵坐标，y=1为红色，y=0为绿色
def plotBestFit(weights):
    n=shape(dataMat)[0] 
    xcord1=[];ycord1=[] #把x2当成y来绘制平面图
    xcord2=[];ycord2=[]
    for i in range(n):
        if dataLebel[i]==1: 
            xcord1.append(dataMat[i][1])
            ycord1.append(dataMat[i][2])
        else:              
            xcord2.append(dataMat[i][1])
            ycord2.append(dataMat[i][2])
    plt.scatter(xcord1,ycord1,c='red') #如果y=1 ，则绘制成红色
    plt.scatter(xcord2,ycord2,c='green')#如果y=0，则绘制成绿色
    x=arange(-3,3,0.1)
    y=(-weights[0,0]-weights[1,0]*x)/weights[2,0] #因为0 = w0+w1*x1+w2*x2,把x2当成y ，得：y = (-w0-w1*x1)/w2
    plt.plot(x,y)
    plt.show()
    
#正式运行测试：
weights = gradAscent(dataMat,dataLebel)
plotBestFit(weights)