微分器相关研究（二）近似改进微分器和Simulink仿真

在上一节中我们进行经典微分器的简单研究，这一节中我们引入状态空间的分析方法

对于经典微分器的传递函数和状态空间表示方法如下，其思路在于利用白噪声期望为0的特点，经过惯性环节较长时间的信号积累，噪声的平均值接近0，从而避免了单步微分计算对噪声的放大 。

 

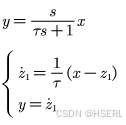
在状态空间的基础上进行离散化，h是积分步长，即采样步长，可以得到

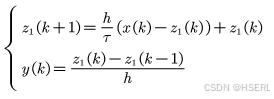
最终的微分信号输出可以表达成下式，当输入x中包含噪声的时候，观察可以得到，此时对噪声的放大系数为 ，仅与微分器参数有关，与采样频率无关 

分别采用100Hz，1000Hz，10000Hz采样频率进行微分器输出仿真，由于采样点数量增加，白噪声的包络更加明显，但是噪声放大系数基本不变。  

 

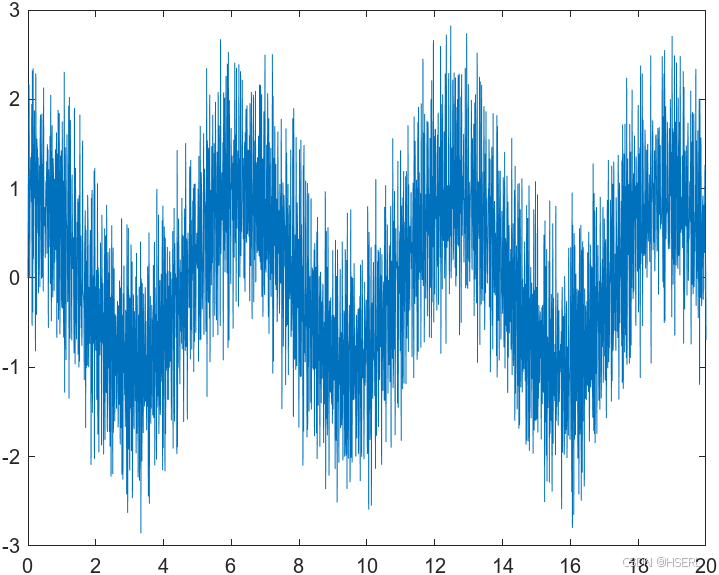
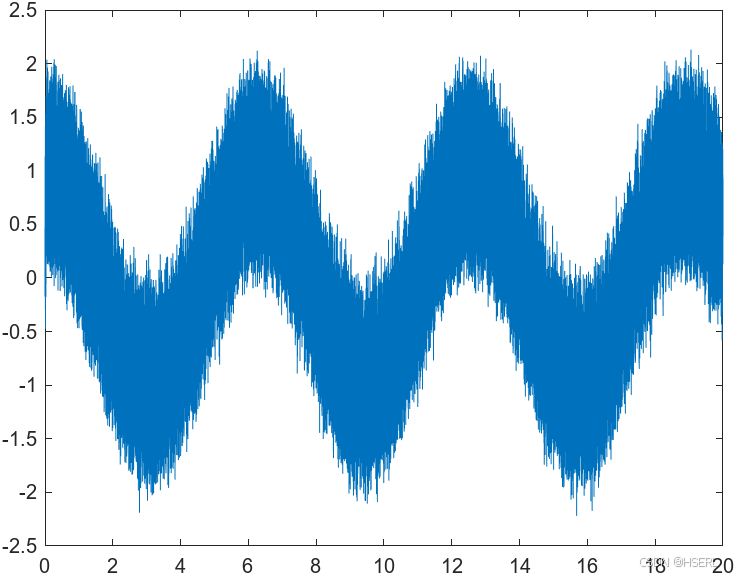
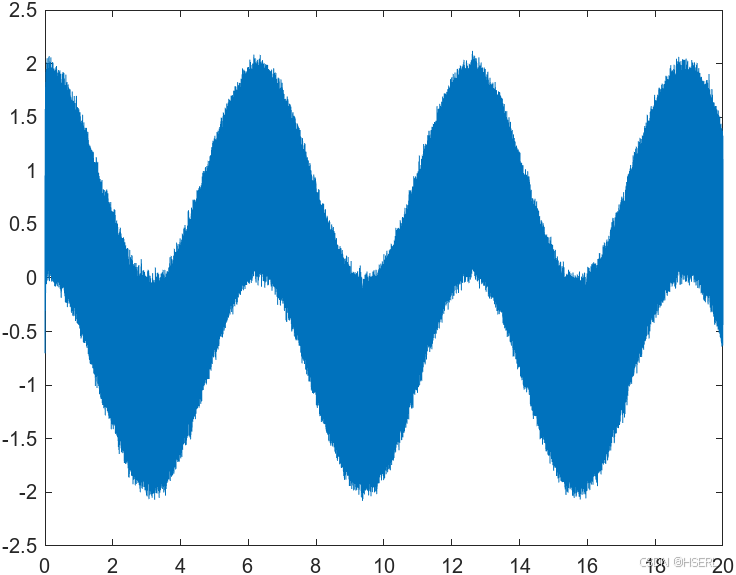
为了减弱噪声放大效应，在原先的基础上采用近似改进的微分器

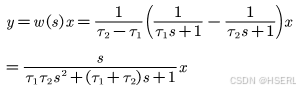
从传递函数上看，当时，该表达式将为一阶与经典微分器一致，当时，即可看作由两个惯性环节组成的微分器，上述我们讲到，采用惯性环节的一个意义在于近似对噪声求积分。经典积分单元直接采用当前响应和惯性环节的输出，当前响应本身带了瞬时的噪声影响，为了消除这部分影响，采用两个不同时间常数的惯性环节，进一步降低白噪声的瞬时影响。 需要注意的是，这里的分析主要针对有效信号是慢时变信号的情况，如果有效信号本身类似于白噪声，则效果大概率不佳。

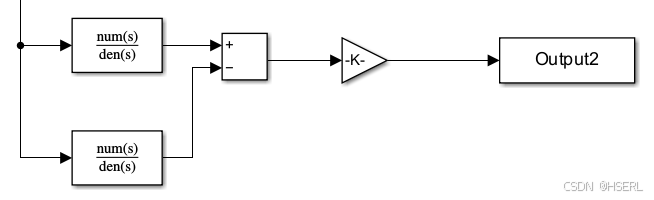
转换成状态空间，并进行离散化

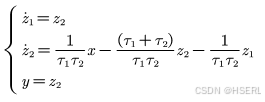
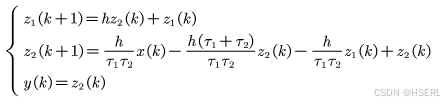
最终的微分信号输出可以表达成下式，当输入x中包含噪声的时候，此时对噪声的放大系数为 ，噪声放大效果与采样频率成反比，与时间常数成正比。 这里就有一个比较好的性质，为了降低系统时延，通常我们需要提高系统的采样频率，经典离散微分方式，随着采样频率升高，噪声的微分放大效果变大，采用该微分器，噪声的微分放大反而能够减小。由于是慢时变有效信号，h即采样步长通常比时间常数 、小得多，故当 、和的量级近似的情况下，改进微分器的噪声抑制效果同样更好

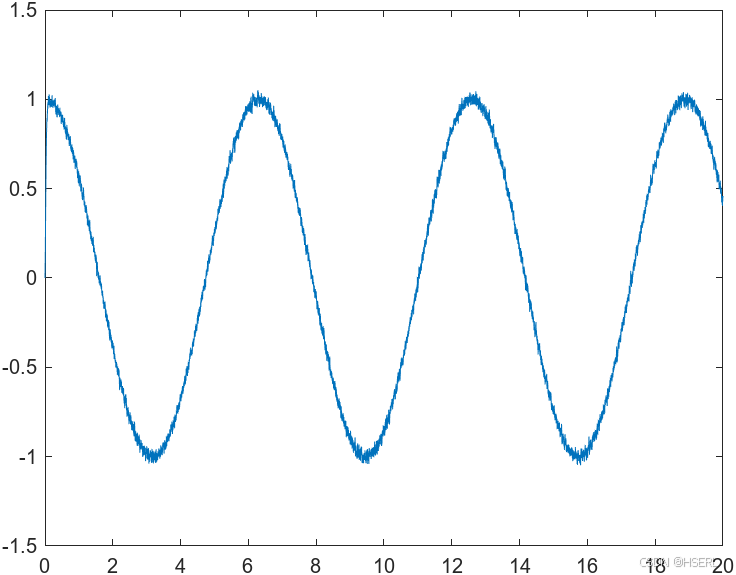
在近似参数的情况下，分别采用100Hz，1000Hz，10000Hz采样频率进行微分器输出仿真

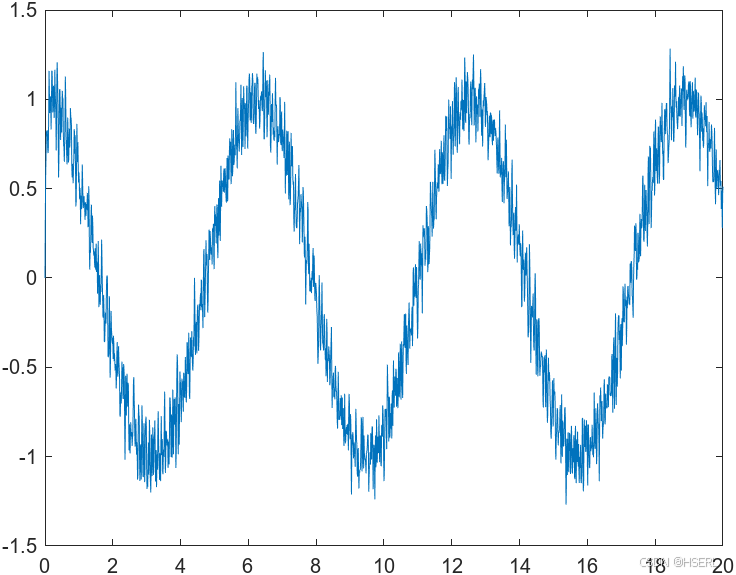
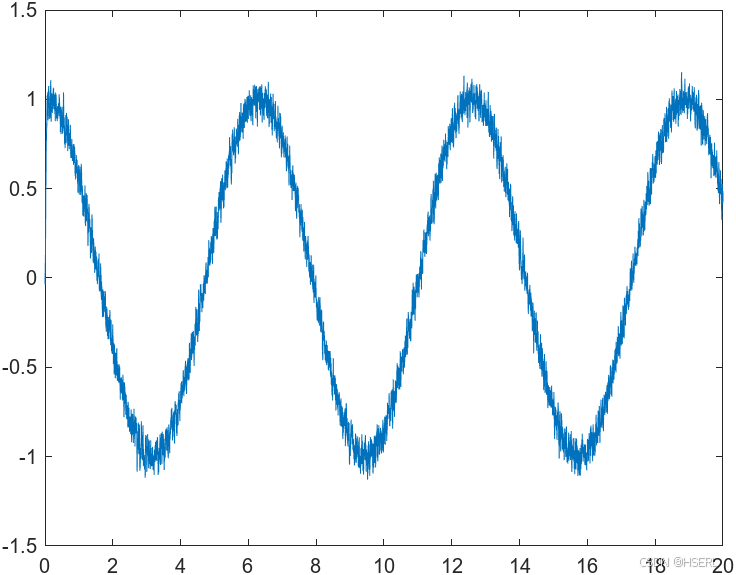
进一步的，我们考虑当当 、很接近的时候，此时，该微分器就可以表示成

记，则有

采用状态空间表示为

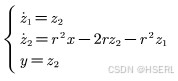
离散化后表示为 

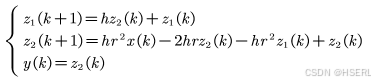
由此进一步的我们可以推测，高阶微分器的表达式为：