微分器相关研究（一）经典微分器和Simulink仿真

微分器作为经典的控制环节具有广泛的应用，然而经典微分环节面临着容易受到噪声干扰，在数字系统中出现高频颤振等问题，面向高精度运动控制的应用，需要针对微分器进行分析和优化。

由于实际实验设备采用Speedgoat，控制框架采用定步长Simulink搭建，故本文采用Matlab结合Simulink进行仿真分析，采样频率5kHz。

在Simulink中有两种典型的微分器结构，分别是连续库中的微分器和离散库中的微分器

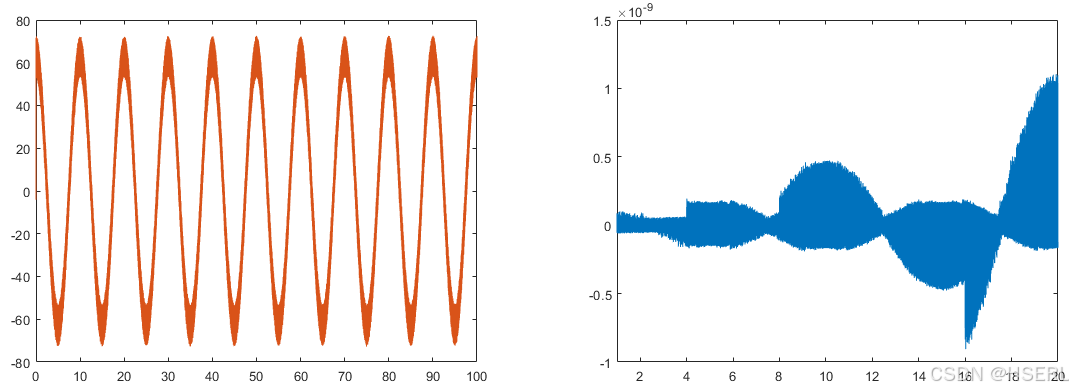
采用设定的正弦叠加白噪声输入信号经过两种微分器，对比输出结果，左图为微分信号时域结果，右图为两者的差值，从数量级上看，可以认为这两种微分器在本场景下几乎一致

进一步的针对集成为微分模块进行分析，在经典调节理论中，对给定信号的微分信号采用如下微分环节得到，式子中的T是比较小的时间常数，其也可以定义为在阶跃响应下，系统输出达到0.63时对应的时间

理论上来讲，当T越小的时候，该环节越接近于理想的微分计算，然而由于数字系统的采样频率受限，实际系统的输入输出都是离散量，当T远小于采样周期的时候，其完全能够模拟微分器的作用，故经典理论采用该环节表征微分器。

然而过小的T会导致噪声被显著放大，在实际应用中该如何根据采样周期选择T，从而平衡噪声放大和微分器效果需要经验调试。对比不同T下的微分信号输出与上述集成模块的输出，当T=0.625ts的情况下，采用该微分环节的结果与集成模块具有最近似的输出。

站在离散的视角看微分计算，可以简单的将微分计算离散化得到

从误差量级看，采用该方法得到的微分信号与集成模块具有更高的相似度，也进一步说明了集成的两种微分器均表现为经典微分器的形式，也面临着经典微分器的问题。