最长公共子序列（LCS）详解（P1439 【模板】最长公共子序列题解）

HYC0907

已于 2024-07-23 14:42:11 修改

阅读量1k

点赞数 38

分类专栏： dp初级问题文章标签： c++ 动态规划算法

于 2024-07-17 20:28:36 首次发布

本文链接：https://blog.csdn.net/HYC0907/article/details/140490482

版权

dp初级问题专栏收录该内容

7 篇文章 0 订阅

订阅专栏

一、做法（暴力）

二、做法（dp）

三、做法（转化LIS）

题目描述

给出 1,2,…，n 的两个排列 $P_{1}$ 和 $P_{2}$ ，求它们的最长公共子序列。

输入格式

第一行是一个数 n。

接下来两行，每行为 n 个数，为自然数 1,2,…，n 的一个排列。

输出格式

一个数，即最长公共子序列的长度。

输入输出样例

输入 #1

5 
3 2 1 4 5
1 2 3 4 5

输出 #1

说明/提示

对于 50% 的数据， n≤10^3；
对于 100% 的数据， n≤10^5。

一、 $n2^{n}$ 做法（暴力）

其实就是通过暴力法去找最长公共子序列。需要先找到所有 $P_{1}$ 的子序列，然后去一一对照是否是 $P_{2}$ 的子序列。 $P_{1}$ 有 $n$ 个元素，那 $P_{1}$ 就有 $2^{n}$ 个子序列，而 $P_{2}$ 则有 $n$ 个元素，所以最后的时间复杂度大于 $O(n2^{n})$ 。代码就不贴了。

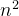二、 $n^{2}$ 做法（dp）

对于前 50% 的数据，我们可以使用动态规划来解决。设f[i][j]表示P1（后面用A表示）和P2（后面用B表示）的最长公共子序列的长度。那么现在有两种状态：

1.A[i] $=$ B[j]。考虑取A中前i-1个元素与B中前j-1个元素的最优解，并加上A[i]和B[j]相等所贡献的1。

2.A[i] $\neq$ B[j]。这里又有两种情况：

①考虑取A中前i-1个元素与B中前j个元素的最优解,也就是不取A[i]，求A[i-1]和B[j]的最长公共子序列。

②考虑取A中前i个元素与B中前j-1个元素的最优解,也就是不取B[j]，求A[i]和B[j-1]的最长公共子序列。

然后判断一下是①大还是②大，取较大值。

我们再看看我们的思路是否满足动态规划的要求：

最优子结构：

要算 A[1]到A[i] 和 B[1]到B[j] 的最长公共子序列的长度，我们需要知道 A[1]到A[i-1]和B[1]到B[j] 、 A[1]到A[i]和B[1]到B[j-1] 、 A[1]到A[i-1]和B[1]到B[j-1] 的最长公共子序列长度。 A[1]到A[i-1]和B[1]到B[j] 、 A[1]到A[i]和B[1]到B[j-1] 的公共子序列都是 A[1]到A[i]和B[1]到B[j] 的公共子序列。如果 A[i]=b[j] 的话， A[1]到A[i-1]和B[1]到B[j-1] 的公共子序列加上 A[i] 也是 A[1]到A[i]和B[1]到B[j] 的公共子序列。

无后效性：

我们并不关心最长公共子序列的样子、怎么得来的，只关心最长公共子序列的长度。

状态：

用 f[i][j] 表示 A[1]到A[i]和B[1]到B[j] 的最长公共子序列长度。

转移：

f[i][j] 可以从3个地方转来：

1.f[i][j] = max( f[i][j] , f[i-1][j] )

2.f[i][j] = max( f[i][j] , f[i][j-1] )

3.如果A[i] = B[j] ，那么 f[i][j] = max( f[i][j] , f[i-1][j-1] + 1 )

没有问题！现在只要弄出方程就行了！

状态转移方程：

$f(i,j)=\left\{\begin{matrix} f(i-1,j-1)+1,A[i]=b[j]\\ max[f(i-1,j),f(i,j-1)],A[i]\neq B[j]\end{matrix}\right.$

根据这个思路，我们可以写出代码。

代码：

#include<bits/stdc++.h>
using namespace std;
int a[100010];
int b[100010];
int f[1010][1010];
int n;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	for(int i=1;i<=n;i++)
	{
		cin>>b[i];
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			f[i][j]=max(f[i-1][j],f[i][j-1]);
			if(a[i]==b[j])
			{
				f[i][j]=max(f[i][j],f[i-1][j-1]+1);
			}
		}
	}
	cout<<f[n][n];
	return 0;
}

三、 $nlogn$ 做法（转化LIS）

但是，由于上面的代码用了两层循环，时间复杂度是 $O(n^{2})$ ，所以当 $n$ 大概在 $10^{5}$ 时就会超时。

我们需要更快的方法！

如果我们把A稍微修改一下呢？

A:3 2 1 4 5

B:1 2 3 4 5

变成

A:① ② ③ ④ ⑤

“1”对应“③”、“2”对应“②”、“3”对应“①”、“4”对应“④”、“5”对应“⑤”

那么B也相对应改变

B:③ ② ① ④ ⑤

这样做后，虽然最长公共子序列的长度没有变，但是A变成单调递增的了。而A与B的子序列一定是A的子序列，所以这个子序列也是单调递增的。

也就是说，如果B中有一个子序列是单调递增的，那么它就是A的子序列。现在我们求的是最长的子序列，谁的最长？B的LIS最长！

所以，我们求的问题就变成了求B的LIS。

对于怎么用 $nlogn$ 的时间去求LIS，可以看我的另外一篇博客：B3637 最长上升子序列题解（详解）

代码：

#include<bits/stdc++.h>
using namespace std;
int a[100010];
int b[100010];
int mp[1000010];
int dp[100010];
int n,R,l,r,mid,ans;
const int inf=0x7fffffff;
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		mp[a[i]]=i;
	}
	for(int i=1;i<=n;i++)
	{
		cin>>b[i];
	}
	dp[0]=0;
	R=0;
	for(int i=1;i<=n;i++)
	{
		if(mp[b[i]]>dp[R])
		{
			dp[R+1]=mp[b[i]];
			R++;
		}
		else
		{
			l=0;
			r=R;
			while(l<=r)
			{
				mid=(l+r)/2;
				if(dp[mid]<mp[b[i]])
				{
					l=mid+1;
				}
				else
				{
					ans=mid;
					r=mid-1;
				}
			}
			dp[ans]=mp[b[i]];
		}
	}
	int t=0;
	for(int i=1;i<=n;i++)
	{
		if(dp[i])
		{
			t++;
		}
	}
	cout<<t;
	return 0;
}