在http://blog.csdn.net/hacker_zhidian/article/details/54898064这一篇博客中总结了一下在求图的最短路中的一个算法-Floyd算法,Floyd算法用于求图的多源最短路径(多源最短路径:图的所有顶点到其他顶点的最短路径),时间复杂度和其他求最短路算法相比较高,如果一些题目只要求求单源最短路径(单源最短路径:图的某个顶点到其他顶点的最短路径)的话,Floyd算法显然不是最好的选择,那么今天我们来看一下另一个用于求单源最短路径的算法:Dijkstra算法。
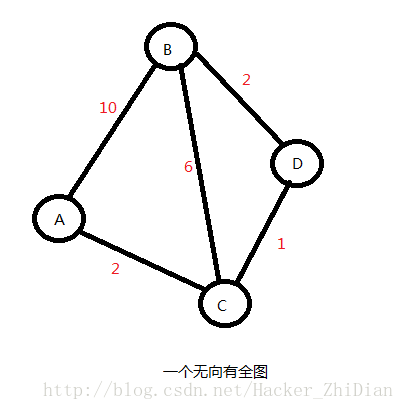
首先我们来看一个图:
图中共有A、B、C、D四个顶点,五条边,假设我们现在要求顶点B到其他顶点的最短路径,依据Dijkstra算法的原理:
首先我们先找到距离顶点B路径最短的顶点,在这个图中很明显距离顶点B路径最短的点为顶点D。之后,将顶点D做上访问标记,并对图中的所有顶点进行检测,看看能否通过顶点D来缩短顶点B到其他顶点的路径。很明显,B–>D–>C(路径为3)这条路的路径小于B–>C(路径为6)这条路的路径,那么我们更新从顶点B到顶点C的最短路径,顶点D的试探结束。我们可以将这个过程称为“缩放”,现在,顶点D的“缩放”结束。之后我们继续寻找距离顶点B路径最短并且没有被标记的顶点,现在距离顶点B路径最短并且没有被标记的顶点为顶点C(顶点D已经被标记了),同样的重复“缩放”过程,直到图中所有的顶点都被标记。
理解了上面的过程,我们就可以架构出大概的Dijkstra算法的代码了:
/*
* n 代表图的顶点总数
* e[][] 代表图的邻接矩阵储存
* book[] 代表标记数组,标记顶点是否已经被选择过
* dis[] 数组储存的是源点距离其他顶点的最短路径
*/
for(int i = 1; i <= n - 1; i++)
{
int min = inf; // inf 为无穷大
int u; // u为当前距离顶点B路径最短的顶点
for(int j = 1; j <= n; j++) // 找到距离顶点B最短的顶点
{
if(book[j] == 0 && dis[j] < min)
{
min = dis[j];
u = j;
}
}
book[u] = 1; // 对要缩放的顶点进行标记
for(int k = 1; k <= n; k++) // 对这个距离顶点B最短的顶点进行缩放
{
if(e[u][k] < inf)
{
if(dis[k] > dis[u] + e[u][k])
{
dis[k] = dis[u] + e[u][k]; // 如果确实可以通过这个顶点的缩放来缩短最短路径,那么更新最短路径
}
}
}
}Ok,算法的核心代码就是这些了,下面给出这个例子的完整代码:
/*
* n 代表图的顶点总数
* e[][] 代表图的邻接矩阵储存
* book[] 代表标记数组,标记顶点是否已经被选择过
* dis[] 数组储存的是源点距离其他顶点的最短路径
*/
#include <iostream>
using namespace std;
const int N = 500;
const int inf = 999999999;
int e[N][N];
int book[N];
int dis[N];
int main()
{
int n, m, s; // 图的顶点总数、边的总数和源节点
cin >> n >> m>> s;
for(int i = 1; i <= n; i++)
{
dis[i] = inf; // 初始化dis数组
for(int j = 1; j <= n; j++)
{
if(i == j)
{
e[i][j] = 0;
}
else
{
e[i][j] = inf;
}
}
}
int x, y, w; // 边的信息
for(int i = 1; i <= m; i++) // 输入边
{
cin >> x >> y >> w;
e[x][y] = e[y][x] = w;
}
dis[s] = 0;
for(int i = 1; i <= n - 1; i++)
{
int min = inf; // inf 为无穷大
int u; // u为当前距离源点路径最短的顶点
for(int j = 1; j <= n; j++) // 找到距离源点最短的顶点
{
if(book[j] == 0 && dis[j] < min)
{
min = dis[j];
u = j;
}
}
book[u] = 1; // 对要缩放的顶点进行标记
for(int k = 1; k <= n; k++) // 对这个距离源点最短的顶点进行缩放
{
if(e[u][k] < inf)
{
if(dis[k] > dis[u] + e[u][k])
{
dis[k] = dis[u] + e[u][k]; // 如果确实可以通过这个顶点的缩放来缩短最短路径,那么更新最短路径
}
}
}
}
for(int i = 1; i <= n; i++) // 输出源点到其他顶点的最短路径
{
cout.width(-5);
cout << dis[i] << " ";
}
cout << endl;
return 0;
}
接下来,我们将给出的例图中的数据输入并运行程序:
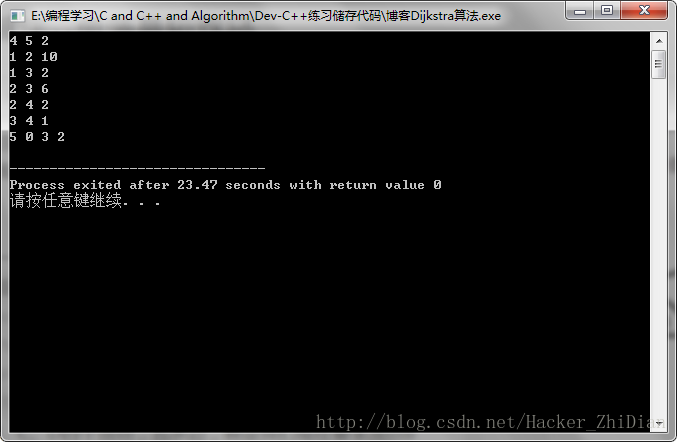
和预想的一样,小伙伴们可以自己尝试一下。
在这里,Dijkstra算法的时间复杂度为O(N^2),确实比Floyd算法小。当然,还有一点要注意,Dijkstra算法是不能解决具有负权边的图的。
如果博客中有什么不正确的地方,还请多多指点。
谢谢观看。。。
























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








