堆

我们在很多情况下都听到“堆”这个计算机术语，那么“堆”到底是什么呢？在数据结构中，堆是一种数据结构，具体一点，最常用的堆就是二叉堆， 二叉堆就是一棵完全二叉树（以下简称堆），我们可以利用这种数据结构来完成一些任务，典型的例子：堆排序就是利用堆来实现的一种高效的排序方式。接下来我们先看一下什么是完全二叉树：

若设二叉树的深度为 h ，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

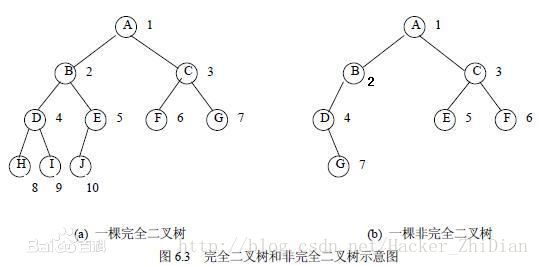
这个定义是百度百科上的，我们并不需要强记，能理解意思就行，我们来看张图：

图片出自百度，我们看一下图中左边的二叉树，这个二叉树就是一棵典型的完全二叉树，这棵二叉树的深度是 4 ， 第 1 ~ 3 层的节点都达到最大个数（节点已满），最后一层的节点从左边开始并且全部持续在在左边。相比，我们再看一下右边的二叉树， 一共有 4 层，但是第三层的 D 节点没有右节点，而 C 节点又存在左右节点，这就已经不符合完全二叉树的定义了。再看最后一层， G 节点并没有从最左边（D节点的左子节点）开始，如果我们要使得它为完全二叉树，我们就要把 G 节点移动到 B 节点的右子节点位置上（作为 B 节点的右子节点）。

仔细观察，我们可以发现：在一个堆中，一个节点的左子节点的下标等于这个节点的下标的两倍，右子节点的下标等于这个节点的下标的两倍加 1 （前提是这个节点存在左右子节点）。
图中左边的完全二叉树 A 节点的下标为 1 ， 而 B 节点的下标为 2 正好等于 A 节点的下标的两倍， C 节点的下标为 3 ，正好等于 A 节点的下标的两倍加一 。同理对于其他的节点也是一样的规律。
这是一个很重要的规律，对堆的操作基本上是基于这个规律来进行的

Ok，接下来我们看两个新概念：最小堆和最大堆。

最小堆：堆顶元素小于堆的任何一个直接子节点。
最大堆：堆顶元素大于堆的任何一个直接子节点。
注意： ①堆中任一子树亦是堆。 ②以上讨论的堆实际上是二叉堆

调整已有数据的数组，使其形成一个堆

好了，说了这么多理论，让我们来看一下怎么去建立一个最大堆：
我们通过代码来看，以下是建立最大堆的核心代码：

// 将堆中以第 i 个节点为根节点的子完全二叉树调整顺序使得其为一个最大堆
void maxHeap(int i, int n) {
    int l, r, large = i;
    l = 2 * i; // 节点的左子节点坐标 
    r = l + 1; // 节点的右子节点坐标 

    /* 
     * 如果当前节点存在左子节点或者右子节点，那么 
     * 找出当前节点、左子节点、右子节点中数值最大的节点的下标 
     */ 
    if(l <= n && heap[l] > heap[large]) { 
        large = l;
    } 
    if(r <= n && heap[r] > heap[large]) {
        large = r;
    }
    // 如果最大值下标不等于这个节点下标，交换，并且对子堆继续调整顺序
    if(large != i) {  
        swap(heap[large], heap[i]);
        maxHeap(large, n);
    }
}

接下来来看一下建立最大堆的完整代码，为了方便，我们不使用下数组中下标为 0 的元素，即数组储存元素从下标 1 开始：

#include <iostream>
using namespace std;
const int N = 10010; // 完全二叉树的最大节点总数 
int heap[N]; // 储存堆的数组 

// 将堆中以第 i 个节点为根节点的子完全二叉树调整顺序使得其为一个最大堆
void maxHeap(int i, int n) {
    int l, r, large = i;
    l = 2 * i; // 节点的左子节点坐标 
    r = l + 1; // 节点的右子节点坐标 

    /* 
     * 如果当前节点存在左子节点或者右子节点，那么分别和左右子节点的值比较
     * 找出当前节点、左子节点、右子节点中数值最大的节点的下标 
     */ 
    if(l <= n && heap[l] > heap[large]) { 
        large = l;
    } 
    if(r <= n && heap[r] > heap[large]) {
        large = r;
    }
    // 如果最大值下标不等于这个节点下标，交换，并且对子堆继续调整顺序
    if(large != i) {  
        swap(heap[large], heap[i]);
        maxHeap(large, n);
    }
}

// 输出我们建立的最大堆 
void print(int a[], int n) {
    for(int i = 1; i <= n; i++) {
        if(i != 1) {
            cout << " ";
        }
        cout << a[i];
    }
    cout << endl;
}

int main() {
    int n;
    cin >> n;
    // 这里采用输入数据的方式为一次性输入所有数据，再调整整个堆
    // 不使用下标为 0 的元素
    for (int i = 1; i <= n; i++) {
        cin >> heap[i];
    }

    /*
     * 从第 n/2 个节点开始对当前子堆的顺序进行调整
     * 建立最大子堆，一直到堆顶（完全二叉树的根节点） 
     * 即为调整已有数据的数组，使其成为一个最大堆
     */ 
    for(int i = n/2; i >= 1; i--) {  
        maxHeap(i, n);
    } 

    print(heap, n);

    return 0;
} 

上面代码中注释中已经写得很清楚了，我们通过一个例子再来理解一下：

假设现在有一个堆中的元素个数为 5 个，分别是： 1 3 4 2 5。
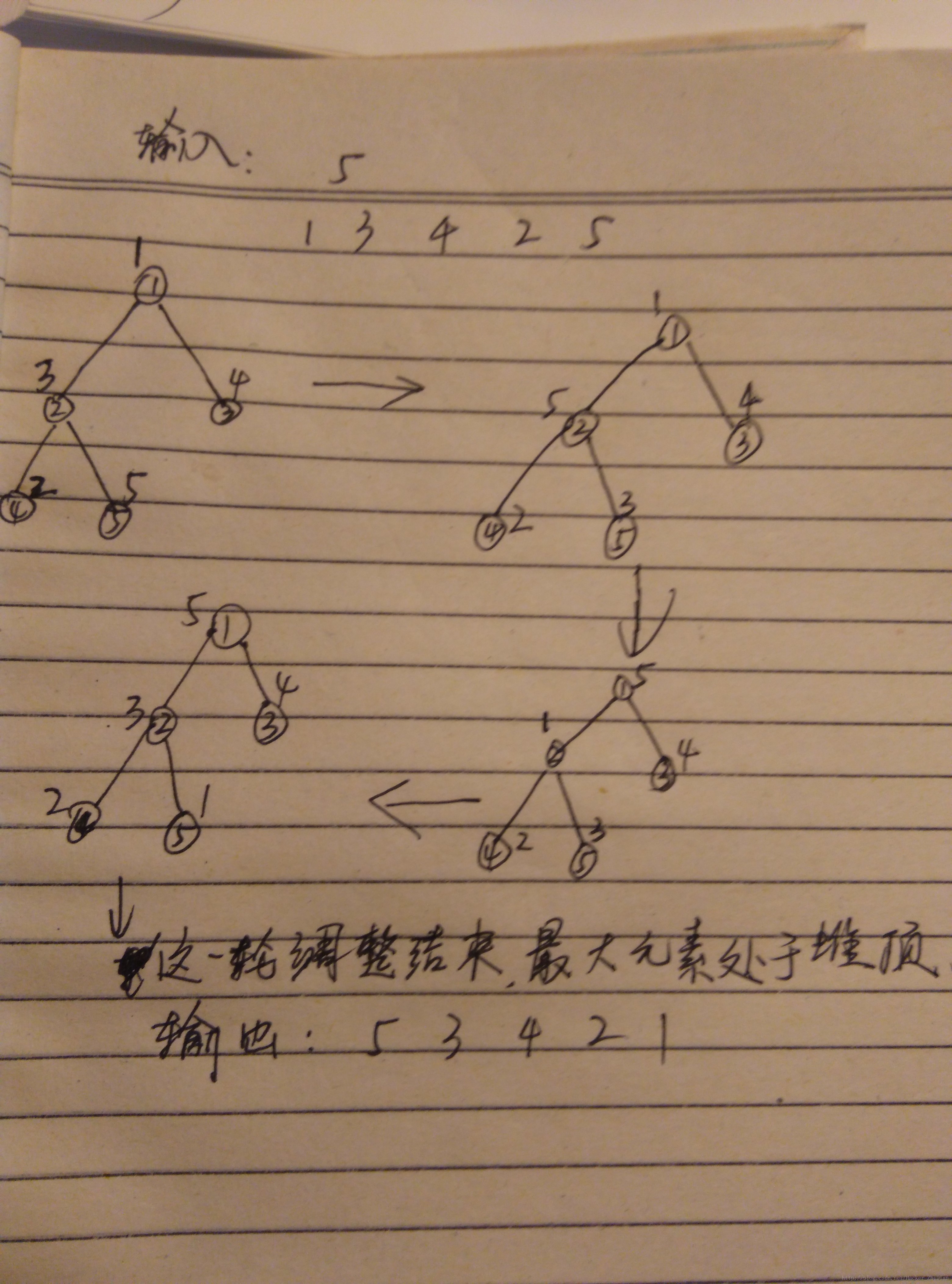
Ok，看图（圆圈里面代表节点所在数组下标，圆圈外面代表节点储存的值）：

这张图是笔者自己模拟的（字一直写不好，多多见谅），圆圈里面的代表当前节点在数组中的下标，圆圈旁边是该下标对应的数值。我们从下标为 2 的节点开始进行调整，经过一轮调整，堆中最大的元素 5 已经位于堆顶，此时将这个堆输出的顺序就是： 5 3 4 2 1

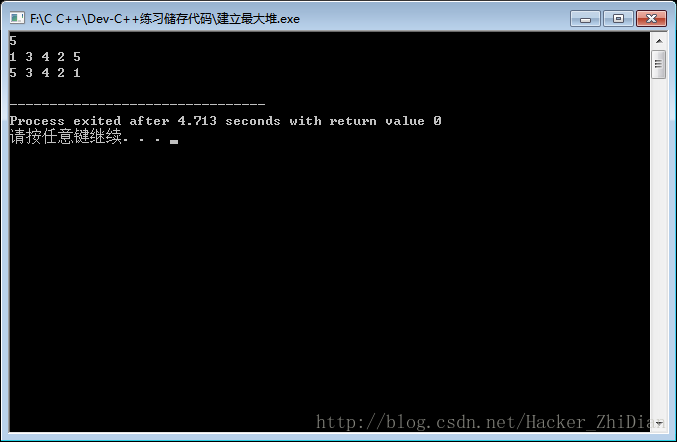
最后，用这个数据测试一下我们的程序：

Nice，和我们模拟的得到的结果符合。

有了最大堆的建立思想，我想最小堆的建立应该也没有什么难度了。这里还是给出建立最小堆的关键代码：

void minHeap(int i, int n) {
    int l, r, small = i;
    l = 2 * i;
    r = l + 1;
    if(l <= n && heap[l] < heap[small]) {
        small = l;
    }
    if(r <= n && heap[r] < heap[small]) {
        small = r;
    }
    if(small != i) {
        swap(heap[small], heap[i]);
        minHeap(small, n);
    }
}

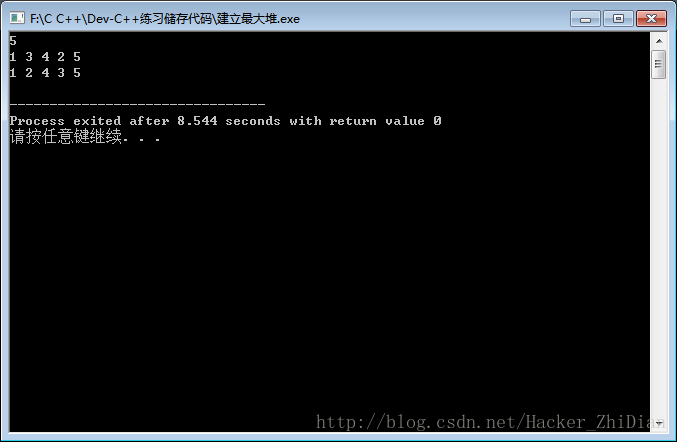
思想和建立最大堆是一样的，注释就不打了。下面是测试数据：

小伙伴们有兴趣可以自己去模拟一下通过这个方法这个最小堆的建立步骤。

逐步插入数据并调整堆

在上面我们是先将整个数据输入到数组中，然后对整个数组再进行调整，使这个数组成为一个堆。但是如果我们需要在每插入一个数据到数组中，就将这个数组调整成堆。该怎么办呢？其实也是差不多，上面我们用的方法是从上到下调整堆，要逐步插入数据我们只需要先将这个数据储存在堆的尾部，然后从下到上调整堆就可以了，
这里以创建最小堆为例子，来看代码：

#include <iostream>
using namespace std;

const int MAXN = 5000010;
int minHeap[MAXN]; // 最小堆，不使用下标为 0 的元素
int curSize = 0; // 当前堆元素个数

// 插入数字到堆尾部并且向上调整堆 
void insertNumber(int num) {
    // 先将元素插入堆尾部 
    minHeap[++curSize] = num;
    // 向上调整堆 
    for (int index = curSize, preIndex = index >> 2;
         preIndex > 0 && minHeap[preIndex] > minHeap[index];
          index = preIndex, preIndex >>= 2) {
        swap(minHeap[index], minHeap[preIndex]);
    }
}

// 向下调整堆，保证最小堆的特性 
// curIndex：当前子堆根结点所在数组下标 
void adjustDown(int curIndex) {
    int curMin = minHeap[curIndex];
    int curMinIndex = curIndex;
    int left = curIndex * 2;
    int right = left + 1;
    // 存在左子结点 
    if (left <= curSize && curMin > minHeap[left]) {
        curMin = minHeap[left];
        curMinIndex = left; 
    }
    // 存在右子节点 
    if (right <= curSize && curMin > minHeap[right]) {
        curMin = minHeap[right];
        curMinIndex = right; 
    }
    // 如果当前较小值节点下标不为 curIndex，
    // 那么交换两个节点的值并且向下调整子堆 
    if (curMinIndex != curIndex) {
        swap(minHeap[curIndex], minHeap[curMinIndex]);
        adjustDown(curMinIndex);
    }
}

// 判断堆是否为空 
bool isEmpty() {
    return curSize <= 0;
} 

// 删除堆顶元素并且重新调整堆，返回堆顶元素 
int removeHeapTop() {
    if (isEmpty()) {
        cout << "堆已为空！" << endl;
        return 0x80000000;
    }
    int result = minHeap[1];
    // 将最尾部的元素提到当前堆顶，作为新的堆顶元素，之后调整整个堆 
    minHeap[1] = minHeap[curSize--];
    adjustDown(1); 
    return result;
}

int main() {
    for (int i = 5; i > 0; i--) {
        // 逐步插入数字来创建最小堆，插入一个数字就向上调整一次
        insertNumber(i);
    }

    while (!isEmpty()){
        // 移除并获取堆顶元素，再向下重新调整堆
        cout << removeHeapTop() << " "; 
    }
    return 0;
} 

来看看结果：

Ok，完成了，到这里我们通过两种方式创建了二叉堆。

关于堆排序我不想在这里总结，虽然我们上面做的很接近堆排序了，但是我还是想把堆排序放在一个排序专栏里面和其他排序方法一起做个总结。这里提示一下堆排序：每一次取出堆顶元素，然后把堆的最后一个元素提到堆顶，然后调用对应的建立最小（最大）堆的方法来维护这个堆，不断重复，直到整个堆为空。

好了，如果博客中有什么不正确的地方，还请多多指点。如果觉得我写得不错，请点个赞表示对我的支持吧。

谢谢观看。。。