微观结构到应用&材料力学行为

---

金属材料力学性能

基本力学性能

服役性能

力学性能
弹性模量
屈服强度
断裂强度

塑性加工成形性能

力学性能	解释
弹性模量	\
流动应力	真实应力,屈服后继续塑性变形并随之升高的抗力
伸长率	\
屈强比	$\frac{{\sigma }_s}{{\sigma }_b}\downarrow$,成形性能$\uparrow$
硬化指数n	用于全量硬化模型,描述应力和应变全量之间的关系
应变速率m	用于增量硬化模型,描述应变增量和应力及应力增量之间随动关系
R值	塑性各向异性
FLD、FLC	板料成形性能评估

失效性能

断裂

• （位错在第二相粒子与基体之间界面塞积,形成裂纹或者第二相和基体的分开,形成空洞）:
  1. 第二相和基体界面对于解离合脱核的阻力
  2. 局部应力集中加速空洞融合
  3. 裂纹分布
• 减少材料中夹杂、气孔、疏松、粗大结晶相，可以提高韧性。
• 合金化和热处理，金属韧性随着强度总体水平增高而降低。

断裂力学选材:是否存在裂纹对强度、断裂方式影响很大

• 断裂韧性$K_c$
• 局部屈服($\frac{\sigma }{{\sigma }_b}<0.7$),塑性修正

疲劳

• 描述
  1. S-N曲线
     耐久应力随循环次数增加而减小
  2. 裂纹扩展速率越低
     合金通过沉淀强化获得抗力强度越多,$\frac{疲劳极限}{抗拉强度}$越低
• 晶界分布致密的位错:机械热处理调控第二相及其分布以提高疲劳性能

---

微结构

微结构类型	描述	解释
相	\	\
晶粒	取向不同的相	晶粒生长、相变、塑性变形
组成	\	\
点缺陷	空位、固溶原子（间隙或者置换）
线缺陷	位错
体缺陷	空隙	裂纹,空洞聚集
织构	多晶体中晶粒取向的首选排列方式	形变织构：大变形造成晶体转动；再结晶织构：择优形核和择优生长；调控织构改变板材塑性应变比r

位错

• ${\tau }_c=KGb{\rho }^{\frac{1}{2}}=KG(\frac{b\gamma }{L}{)}^{\frac{1}{2}}$
• 随着位错密度$\rho$的增加(变形量增加)或者位错运动自由程L的减少,临界切分应力增加,强度提高

因素		解释
位错密度	加工硬化	位错塞积:F-R机制产生可动位错被阻碍形成不可动位错 ${\rho }_i$,位错纠缠:高位错密度区缠结发展成为亚晶,形成位错变形胞
${\gamma }_{SFE}$		界面能$\downarrow$,不可动位错增加,晶粒尺寸减小
形变热效应	随着变形量增加,形变热效应越明显	诱发位错的非保守运动(转变滑移系,攀移),不可动位错转化为可动位错,不可动位错密度${\rho }_i\downarrow$

晶粒

• 晶粒大小
  晶界是位错运动阻碍，减小晶粒尺寸，障碍数目增加.

  细化晶粒，${\sigma }_s\uparrow$，满足霍尔-佩奇公式：${\sigma }_s={\sigma }_i+k_y{d}^{-\frac{1}{2}}$(bcc金属$k_y$高,细晶强化效果最好)
  增大过冷度 ：对形核率的提高大于对晶体生长速率的提高，晶粒数增多
  变质处理：加入细小的形核剂（钛、锆）
  震动搅拌：增大能量起伏，使枝晶碎断，增加晶核数量

• 晶粒不均匀性和变形不同时性

  1. 不同时性：各晶粒取向不同，即$\cos \varphi cos\lambda$不同，导致应力状态不同，取向有利的晶粒先考试滑移变形，而取向不利的晶粒可能仍处于弹性变形状态。
  2. 不均匀性：多相合金，各相晶粒力学性能差异导致基体与第二相变形量不同。
  3. 金属组织愈不均匀，塑性变形不同时性愈显著，局部愈容易达到塑性极限形成裂纹；当外力增大时，滑移从某些晶粒传播到另外一些晶粒，不断传播产生宏观可见的塑性变形

• 各晶粒变形相互协调性

  1. 多晶体作为一个整体，不允许晶体仅在一个滑移系中变形，否则将造成晶界开裂
  2. 每个晶粒必须同时至少五个独立的滑移系开动或者滑移同时进行孪生变形，才能确保产生任何方向不受约束的体积不变（晶界不开裂）的塑性变形。

多晶体应变硬化速率比相同的单晶体金属要高；	Hcp滑移系少，变形不易协调，故其塑性极差；	金属间化合物滑移系更少，变形更不易协调，性质更脆

• 晶界:晶界能影响
• 亚结构

加工硬化

退化\再结晶:
$\sigma =k{\epsilon }^n$
热变形:
$\sigma =k({\epsilon }_0+\epsilon {)}^n$
屈服强度增加，抗拉强度增加，伸长率减小

固溶

间隙固溶强化效果大于置换固溶；
且在bcc金属中点阵畸变属于非对称性的，强化效果强于在fcc

要求	解释
冷却后保持在固溶体中，不与其他元素反应生成不溶物	1. 形成晶格畸变，阻碍位错运动，固溶强化
原子半径差异大	2. 溶质原子和基体金属原子尺寸、价电子数目相差越大，固溶效果越明显
退火温度下具有明显的溶解度	3.间隙原子固溶度有限，实际强化效果也有限

显著提高屈服强度${\sigma }_s$、拉伸强度${\sigma }_b$和高温下得抗蠕变能力(高温强度)，但韧性和塑性却有所下降

第二相:析出\沉淀强化

尺寸、形状、数量、分布

分析因素	解释
晶体学匹配程度	共格、半共格、非共格
第二相大小	两种机制晶粒尺寸-屈服强度曲线的交点强度最高

• 不可变形第二相（绕过机制）
• 可变形第二相（切过机制）

---

性能

单晶体塑性

• 位错
• 孪生 低温和高速率下变形 （为什么 ）
• 屈服 $f({\sigma }_{ij},{\epsilon }_{ij},T,\dot{(}{\epsilon }_{ij}))$=C

因素	作用
应变速率m	$\sigma =C{\dot{\epsilon }}^m$，应变速率大，${\sigma }_s\uparrow$，塑性$\downarrow$
温度	温度上升，${\sigma }_s\downarrow ,塑性\uparrow$

温度越高，对应变速率越敏感

• 断裂

强度理论	描述
拉应力强度理论	最大拉应力是引起断裂的主要原因
最大伸长线应变理论	最大伸长线应变是引起断裂的主要原因
最大切应力理论	最大切应力是引起物体屈服的主要原因
畸变能密度理论	认为不管材料的应力状态，只要畸变能密度达到与材料性质有关的一个极限值就发生屈服

---

弹塑性力学

应力分析

• 平面应力状态旋转
  ${\sigma }_{x^{\prime }}=\frac{{\sigma }_x+{\sigma }_y}{2}+\frac{{\sigma }_x-{\sigma }_y}{2}cos2\theta +{\tau }_{xy}sin2\theta$
  ${\sigma }_{y^{\prime }}=\frac{{\sigma }_x+{\sigma }_y}{2}-\frac{{\sigma }_x-{\sigma }_y}{2}cos2\theta -{\tau }_{xy}sin2\theta$
  ${\tau }_{x^{\prime }{y}^{\prime }}=-\frac{{\sigma }_x-{\sigma }_y}{2}+{\tau }_{xy}cos2\theta$
• 任意平面应力${\sigma }_n$
  考虑面积不同对应力影响影响
  $S_x={\sigma }_{x}cos(n,x)+{\tau }_{yx}cos(n,y)+{\tau }_{zx}cos(n,z)$
  $S_y={\sigma }_{y}cos(n,y)+{\tau }_{xy}cos(n,x)+{\tau }_{zy}cos(n,z)$
  $S_z={\sigma }_{z}cos(n,z)+{\tau }_{xz}cos(n,x)+{\tau }_{yz}cos(n,y)$
  再考虑投影
  ${\sigma }_n=S_{x}l+S_{y}m+S_{z}n={\sigma }_x{l}^2+{\sigma }_y{m}^2+{\sigma }_z{n}^2+2({\tau }_{xy}lm+{\tau }_{xz}ln+{\tau }_{yz}mn)$
  从而，任意平面切应力为
  ${\tau }_n^2=S^2-{\sigma }_n^2$
• 三向应力状态变换
  ${\sigma }_{ij}^{\prime }=g\cdot {\sigma }_{ij}\cdot g^T$
• 主应力
  求解方程${\sigma }^3-I_1{\sigma }^2+I_2\sigma -I_3=0$,
  其中,
  $\{\begin{array}{l}{I}_1={\sigma }_x+{\sigma }_y+{\sigma }_z\\ I_2={\sigma }_x{\sigma }_y+{\sigma }_y{\sigma }_z+{\sigma }_z{\sigma }_x-{\tau }_{xy}^2-{\tau }_{yz}^2-{\tau }_{xz}^2\\ I_3={\sigma }_x{\sigma }_y{\sigma }_z+2{\tau }_{xy}{\tau }_{yz}{\tau }_{zx}-{\sigma }_x{\tau }_{yz}^2-{\sigma }_y{\tau }_{zx}^2-{\sigma }_z{\tau }_{xy}^2\end{array}$
  平面状态
  ${\sigma }_{1,2}=\frac{{\sigma }_{11}+{\sigma }_{22}}{2}$
• 最大剪应力
  ${\tau }_{max}=max(|{\tau }_{12}|,|{\tau }_{13}|,|{\tau }_{23}|)$
• 应力张量分解
  ${\sigma }_m=\frac{1}{3}({\sigma }_x+{\sigma }_y+{\sigma }_z)$
• 应力莫尔圆
• 八面体应力
  
  
• 等效应力
  ${\sigma }_e=\frac{3}{\sqrt{2}}{\tau }_8$(标量)
  等效实质:弹性应变能等效
  等效形式:复杂应力状态和简单应力状态(一维)等效
• 应力平衡微分方程

应变分析

• 几何方程:位移和应变之间的关系
  1. 二维
     $\{\begin{array}{l}{\epsilon }_x=\frac{\partial u}{\partial x}\\ {\epsilon }_y=\frac{\partial v}{\partial y}\\ \gamma {}_{xy}=\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\end{array}$
  2. 热应变
     ${\epsilon }_i^T={\alpha }_T\Delta T$
     ${\gamma }_{ij}^T=0$
• 任意方向正应变${\epsilon }_N$
  已知${\epsilon }_x,{\epsilon }_y,{\gamma }_{xy}$，求任意方向线应变${\epsilon }_N$和线段夹角变化.
  ${\epsilon }_N={\epsilon }_x{l}^2+{\epsilon }_y{m}^2+lm{\gamma }_{xy}$
  
• 主应变

${\epsilon }_{max}=max(|{\epsilon }_{12}|,|{\epsilon }_{23}|,|{\epsilon }_{31}|)$

• 八面体应变
  线应变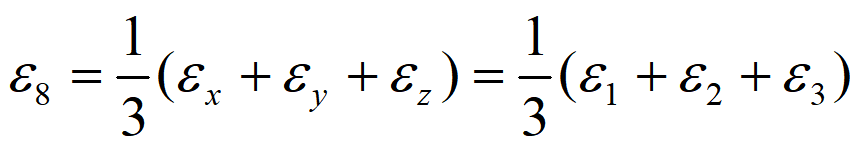
  剪应变
  

• 等效应变
  

• 应变协调方程

  $\frac{{\partial }^2{\epsilon }_x}{\partial y^2}+\frac{{\partial }^2{\epsilon }_y}{\partial x^2}=\frac{{\partial }^2{\gamma }_{xy}}{\partial x\partial y}$

平面问题

• Hooke定律

• 平面问题物理方程(Hooker方程):
  

• 相容方程

1. 有体力
   平面应力:
   
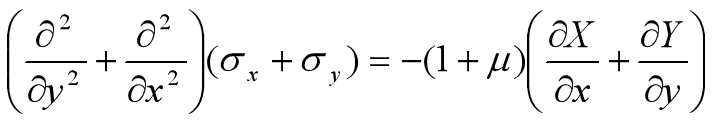
   平面应变:
   
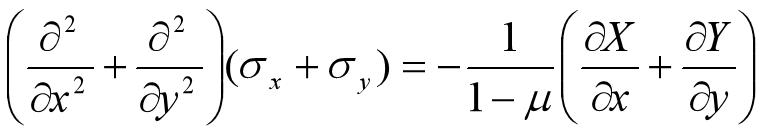
2. 无体力
   
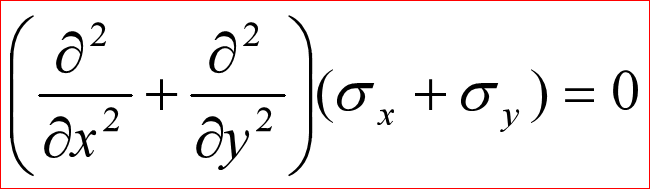
   体力转化为面力

• 双调和方程
  ${\nabla }^4\phi =\frac{{\partial }^4\phi }{\partial x^4}+\frac{{\partial }^4\phi }{\partial x^4}+2\frac{{\partial }^4\phi }{\partial x^2\partial y^2}=0$
  $\{\begin{array}{l}{\sigma }_x=\frac{{\partial }^2\phi }{\partial y^2}\\ {\sigma }_y=\frac{{\partial }^2\phi }{\partial x^2}\\ \tau =-\frac{{\partial }^2\phi }{\partial x\partial y}\end{array}$