线段树（原数组的单点维护+区间查询）

线段树

基本的概念，如果已经大概了解线段树是什么或者你对理论不感兴趣的就可以直接跳到步骤3、分步图解实现

1、定义

• 线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。

• 对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

• 使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为O(logN)。而未优化的空间复杂度为2N，实际应用时一般还要开4N的数组以免越界，因此有时需要离散化让空间压缩。

---

2、基本结构

• 线段树是建立在线段的基础上，每个结点都代表了一条线段[a,b]。长度为1的线段称为元线段。非元线段都有两个子结点，左结点代表的线段为[a,(a + b) / 2]，右结点代表的线段为[ ( (a+b)/2 )+1,b]。

• 长度范围为[1,L] 的一棵线段树的深度为log(L) + 1。这个显然，而且存储一棵线段树的空间复杂度为O(L)。

• 线段树支持最基本的操作为插入和删除一条线段。下面以插入为例，详细叙述，删除类似。

• 将一条线段[a,b] 插入到代表线段[l,r]的结点p中，如果p不是元线段，那么令mid=（l+r）/2。如果b<mid，那么将线段[a,b] 也插入到p的左儿子结点中，如果a>mid，那么将线段[a,b] 也插入到p的右儿子结点中。

• 插入（删除）操作的时间复杂度为O(logn)。

---

3、分步图解实现

(1)、整颗线段树

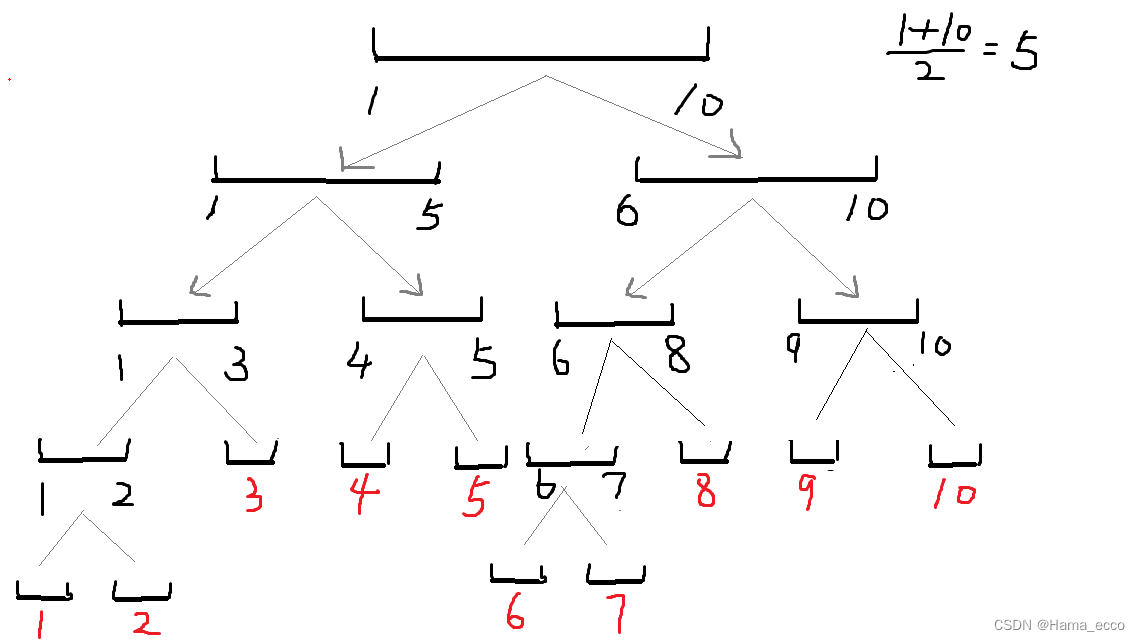
如图所示，以数组举例：

• 每个结点代表一段数组下标的值的求和。（例如图中1-10代表a[1]+a[2]+...+a[10]）
• 则每个结点的子节点（如果有子节点的话）代表这个节点的一半长度。
• 一直到延伸此到某个节点代表的长度为1为止，且这个节点没有子节点。

那么怎么找节点呢？

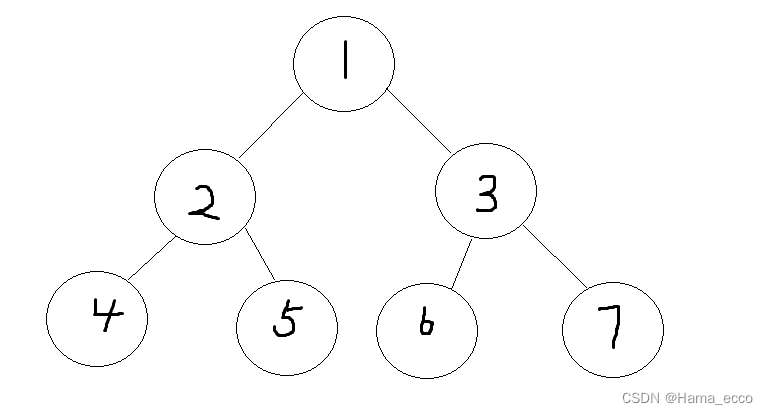
二叉树中，若父节点为标号为k，则其左子节点标号为2k，右子节点标号为2k+1

所以我们整颗线段树可以看成一个二叉树。我们用f[]来表示（下面所有样例均以d[]来表示）

---

(2)、区间查询

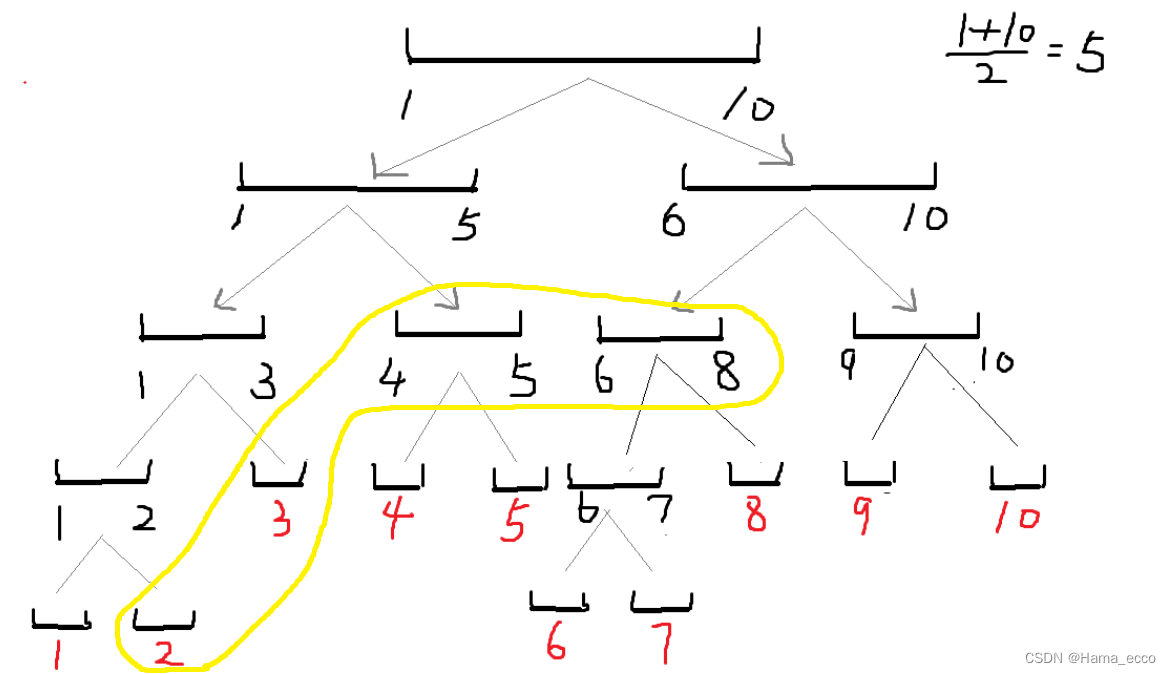
以数组举例，若我们查询数组下标2至8的和，只需要查询下图黄圈所标注的（ f[x]中x的求得请移步(1)中二叉树找结点 ）：

• 2线段 = f[17] = 代表a[2]

• 3线段 = f[9] = 代表a[3]

• 4-5线段 = f[5] = 代表a[4]+a[5]

• 6-8线段=f[6]=代表a[6]+a[7]+a[8]

只需查询f[]4次

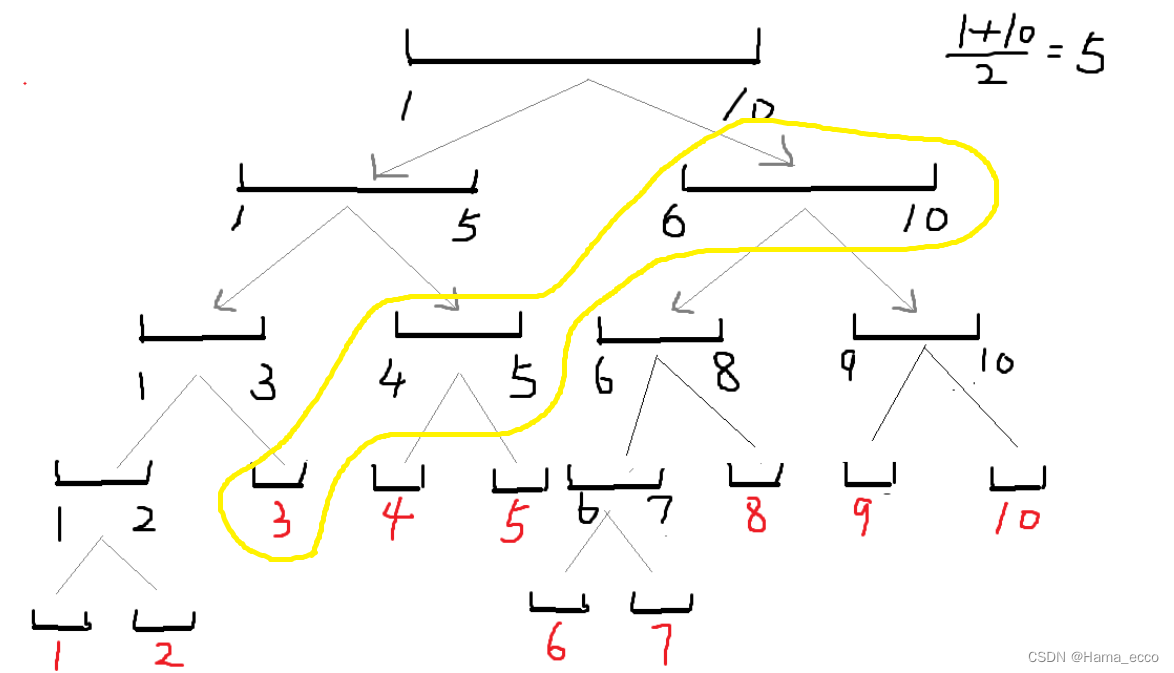
同理若查询数组下标3-10的和，只需查询下图黄圈所标注的：

• 3线段 = f[9] = 代表a[3]

• 4-5线段 = f[5] = 代表a[4]+a[5]

• 6-10线段 = f[3] = 代表a[6]+a[7]+...+a[10]

只需查询f[]3次

---

(3)、修改

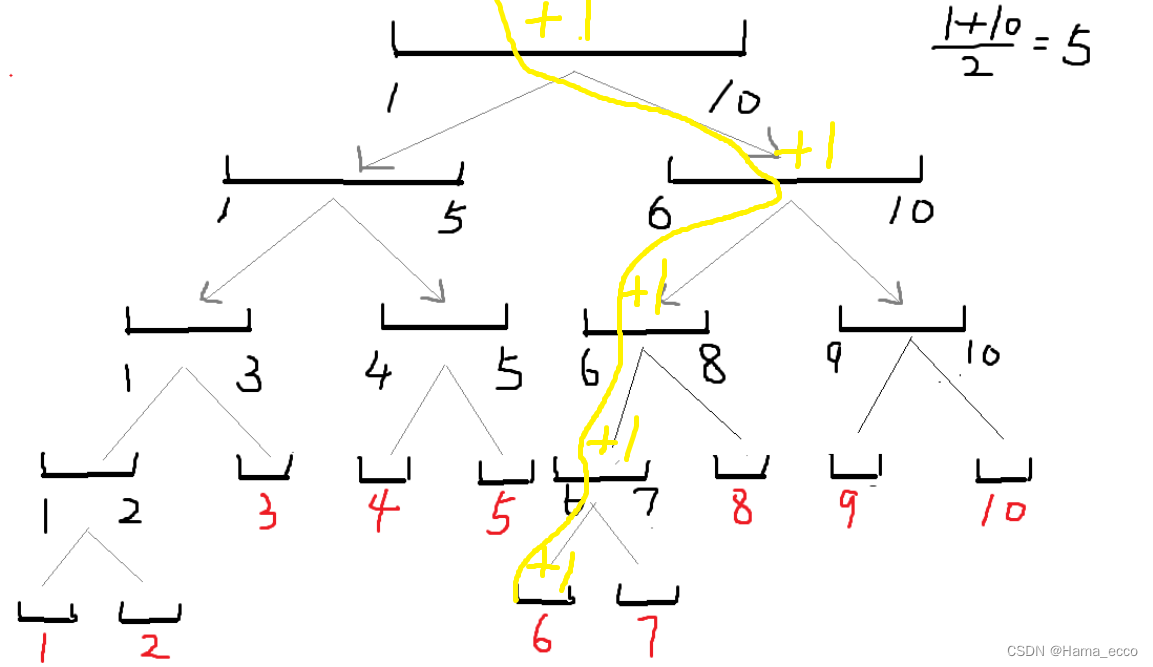
以数组为例，若增加数组下标为6的值：

a[6]+=1

如下图黄线经过的包含6的路径所代表的的f[]全部+1；

1-10线段: f[1]+=1;

6-10线段: f[3]+=1;

6-8线段: f[6]+=1;

6-7线段: f[12]+=1;

6线段: f[24]+=1

我们注意到6线段是用f[24]代表的，而2线段是用f[17]代表的，为什么不用f[18]代表呢？

是因为我们这个未优化线段树默认结点都是有子节点的，也就是说下图中3线段也是有子节点的，但3已经不能再划分，所以我们默认3线段可以划分成两个空值子节点。此操作也符合线段树的结点下标的查找。

---

4、分步代码实现

1、建立线段树

	for(int i=1;i<=n;i++){
		scanf("%d", &a[i]);
	}
	buildtree(1,1,n);//定义一个函数来建立线段树

    inline void buildtree(int k ,int l ,int r){//当前这个点的标号为k,区间左端点为l,右端点为r 
        if(l == r) {
            f[k] = a[l];
            return;
        }
        int m = (l + r) >> 1;//int m = (l+r)/2;
        buildtree(k + k , l, m);
        buildtree(k + k + 1 , m + 1, r);
        f[k] = f[k + k]+f[k + k + 1];
    }

怎么理解这个程序呢？

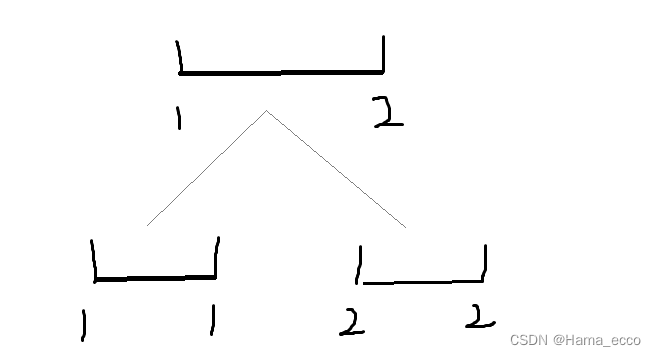
如上图，拿数据简单的来举例；

• f[1] 代表 1-2线段

• 我们所声明的函数为buildtree(int k ,int l ,int r)表示当前这个点的标号为k,区间左端点为l,右端点为r

• 则我们用buildtree(1,1,n)来表示从d[1]开始建里线段树，且f[1]代表l-r的值

以上图1-2线段举例:

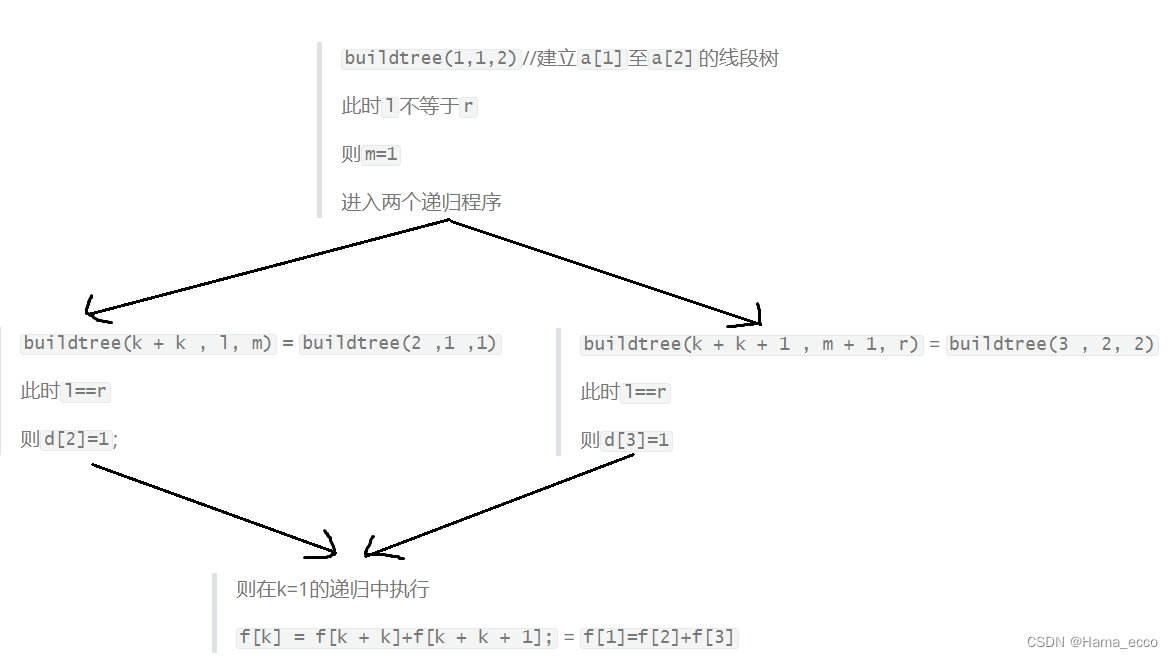
也就是说，建立线段树是先有了最小线段f[x+x]和f[x+x+1]的值后才有f[x]的值，当然这个不需要深度理解。

---

2、区间查询

我们若查询a[x]到a[y]的区间和：

	calc(1,1,n,x,y);//在1-n的范围中，找到x-y范围的和

    int calc(int k,int l,int r,int s,int t){		//结点为k,在l-r的区间中找到目标区间s-t区间的和
        if(l==s&&r==t)		//如果l==s&&r==t则此k代表的范围l-r就是所要查询的目标区间s-t区间，则返回f[k]
            return f[k];
        int m = (l+r)>>1;		//计算中值
        if(t <= m)
            return calc(k+k,l,m,s,t);		//若所需要查询的目标区间的右端点小于等于中值m的，则去左子节点中继续寻找目标结点
        else		//若所需要查询的目标区间的右端点大于中值，说明所求目标区间有两种情况
            if(s>m)		//第一种情况就是目标区间完全在右子节点
                return calc(k+k+1,m+1,r,s,t);
            else		//第二种情况就是目标区间部分在左子节点，另一部分在右子节点
                return calc(k+k,l,m,s,m)+calc(k+k+1,m+1,r,m+1,t);
    }

强烈推荐代入一组简单数据（例如上图的那个1-2）自己理解一下。

3、单点维护

我们若将a[x]+=y

add(1, 1, n, x, y)

    inline void add(int k,int l,int r,int x,int y){//要在下标为k的点,对应的区间为l-r, 下标为x的点+y; 
        f[k]+=y;//下标为k的区间一定包含x 
        if(l == r)	
            return;
        int m = (l+r) >>1;
        if(x<=m)//左面 
            add(k+k, l, m, x, y);
        else//右面 
            add(k+k+1, m+1, r, x, y); 
    } 

同理还是推荐代入简单数据理解！

5、完整代码：

依次输入n和m，表示n个数组和m次操作。

依次输入n个数，代表原数组的值。

依次输入m行，每行三个数字t，x，y；

当t==1时，将a[x]+=y;

当t==2时，输出a[x]+...+a[y]的区间和

#include<bit/stdc++.h>

using namespace std;

int n,m,a[500001],t[2000001];//n是点数，m是操作数 

inline void buildtree(int k ,int l ,int r){//当前这个点的标号为k,区间左端点为l,右端点为r 
	if(l == r) {
		f[k] = a[l];
		return;
	}
	int m = (l + r) >> 1;
	buildtree(k + k , l, m);
	buildtree(k + k + 1 , m + 1, r);
	f[k] = f[k + k]+f[k + k + 1];
}

inline void add(int k,int l,int r,int x,int y){//要在下标为k的点,对应的区间为l-r, 下标为x的点+y; 
	f[k]+=y;//下标为k的区间一定包含x 
	if(l == r)	
		return;
	int m = (l+r) >>1;
	if(x<=m)//左面 
		add(k+k, l, m, x, y);
	else//右面 
		add(k+k+1, m+1, r, x, y); 
} 

int calc(int k,int l,int r,int s,int t){
	if(l==s&&r==t)
		return f[k];
	int m = (l+r)>>1;
	if(t <= m)
		return calc(k+k,l,m,s,t);
	else
		if(s>m)
			return calc(k+k+1,m+1,r,s,t);
		else
			return calc(k+k,l,m,s,m)+calc(k+k+1,m+1,r,m+1,t);
}

int main(){
	
	scanf("%d%d", &n, &m);
	for(int i=1;i<=n;i++){
		scanf("%d", &a[i]);
	}
	buildtree(1,1,n);
	
	for(int i=1;i<=m;i++) {
		int t,x,y;
		scanf("%d%d%d",&t,&x,&y);
		if(t == 1)	
			add(1, 1, n, x, y);//1号点对应的1-n区间,下标是x,修改的值是y 
		else
			printf("%d\n",calc(1,1,n,x,y) );//查询x-y区间的和 
	}
	
	return 0;
}