关于斐波那契数列的讲解

最新推荐文章于 2025-03-08 22:54:44 发布

哈里•波特

最新推荐文章于 2025-03-08 22:54:44 发布

阅读量696

点赞数

文章标签： python

本文链接：https://blog.csdn.net/Hanson1019/article/details/131026279

版权

斐波那契数列是一个在数学、计算机科学等领域有广泛应用的数列，每一项都是前两项之和。本文介绍了斐波那契数列的概念，起源以及一个使用递归方法的Python代码示例，展示了如何生成并打印斐波那契序列的一部分。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

今天我们来讲一下斐波那契数列。

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=1，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）在现代物理、准晶体结构、化学等领域，斐波那契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波那契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

中文名：斐波那契数列

外文名：Fibonacci sequence

别名：黄金分割数列、兔子数列

表达式：F[n]=F[n-1]+F[n-2](n>=2,F[0]=1,F[1]=1)

提出者：莱昂纳多·斐波那契

提出时间：1202年

适用领域:代数

应用学科:数学

定义：斐波那契数列指的是这样一个数列：1，1，2，3，5，8，13，21，34，55，89... 自然中的斐波那契数列这个数列从第3项开始，每一项都等于前两项之和。斐波那契数列的定义者，是意大利数学家莱昂纳多·斐波那契（Leonardo Fibonacci），生于公元1170年，卒于1250年，籍贯是比萨。他被人称作“比萨的莱昂纳多”。1202年，他撰写了《算盘全书》（Liber Abacci）一书。他是第一个研究了印度和阿拉伯数学理论的欧洲人。他的父亲被比萨的一家商业团体聘任为外交领事，派驻地点于阿尔及利亚地区，莱昂纳多因此得以在一个阿拉伯老师的指导下研究数学。他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯等地研究数学。另外斐波那契还在计算机C语言程序题中应用广泛。

自然中的斐波那契数列：

注：以下内容来自百度

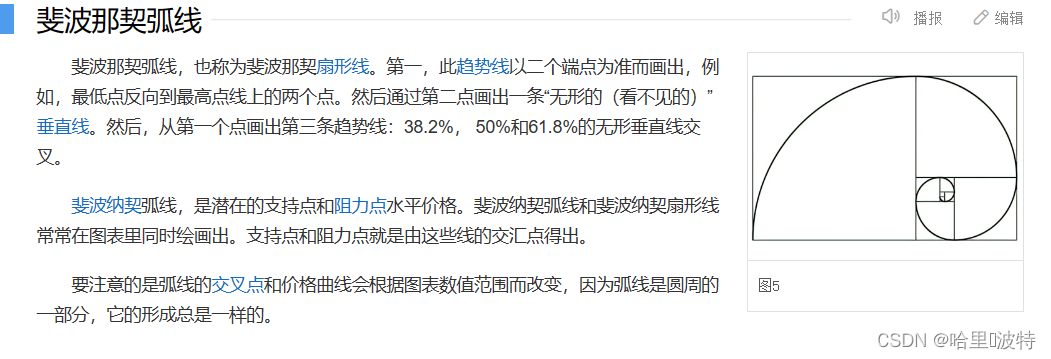
下面是实验舱的斐波那契数列的代码：

# 舞台自动重置,kpen和p可直接使用.
import random
from math import*
def Fibonacci_Recursion_tool(n):#斐波那契数列方法
	if n<=0:
		return 0
	elif n==1:
		return 1
	else:
		return Fibonacci_Recursion_tool(n-1)+Fibonacci_Recursion_tool(n-2)
def Fibonacci_Recursion(n):#生成斐波那契数列，并存入列表
	result_list=[]
	for i in range(1,n+3):
		result_list.append(Fibonacci_Recursion_tool(i))
	return result_list
yu=Fibonacci_Recursion(10)#生成斐波那契数列
print(yu)
p.draw()