哈密尔顿蒙特卡洛（Hamiltonian Monte Carlo）

最新推荐文章于 2025-05-22 20:53:17 发布

阿喵酱紫糖

最新推荐文章于 2025-05-22 20:53:17 发布

阅读量4.8k

点赞数 2

分类专栏：机器学习文章标签：深度学习

原文链接：https://bocaiwen.github.io/Hamiltonian-Monte-Carlo.html

版权

机器学习专栏收录该内容

34 篇文章

订阅专栏

哈密尔顿蒙特卡洛（Hamiltonian Monte Carlo）

Metropolis-Hastings 采样方法的一个问题是它会展现出随机漫步式的行为，而随机漫步对参数空间的探索效率并不高——平均来说探索的距离与步数的平方根成正比（n−−√n，参考 Random Walks in 1 dimension）。而简单的扩大步幅又会降低接受率。哈密尔顿蒙特卡洛（HMC）方法提供了一个新思路，即可以提高参数空间的探索效率，又能保持较高的接受率。

哈密尔顿动力学

介绍 HMC 采样方法之前需要先简单说一下哈密尔顿动力学。

哈密尔顿（爱尔兰人 1805-1865）在拉格朗日力学的基础上对经典的牛顿力学做了全新的解释。牛顿力学强调，加速度，作为力作用到物体上的效果，是位置（距离）对时间的二阶导数。引入速度可以把二阶导分解成两个一阶导：速度是位置（距离）对时间的一阶导数，而加速度是速度对时间的一阶导数。

考虑地球引力与物体组成的动力系统。每个单位重量（m=1m=1）的物体在高度为 hh 的地方具有势能（potential energy） Ep(h)=mgh=ghEp(h)=mgh=gh，其中 gg 为加速度，也是重力，且 g=∂Ep∂hg=∂Ep∂h。在物体自由落体的时候（忽略空气阻力等其他因素），物体的速度对时间的导数也是 gg，即 dvdt=gdvdt=g。所以速度对时间的导数等于势能对位置（高度）的导数：dvdt=∂Ep∂hdvdt=∂Ep∂h。

而单位重量（m=1m=1）的物体运动中的动能（kinetic energy）为 Ek(v)=mv22=v22Ek(v)=mv22=v22，动能对速度的导数是 ∂Ek∂v=v∂Ek∂v=v。同时速度又是位置（高度）对时间的导数 dhdt=−vdhdt=−v，其中负号表示反向（速度增加对应高度降低）。所以位置（高度）对时间的导数等于反向的动能对速度的导数 dhdt=−∂Ek∂vdhdt=−∂Ek∂v。

考虑势能和动能组成的能量系统：H(h,v)=Ep(h)+Ek(v)H(h,v)=Ep(h)+Ek(v)，其中 HH 是哈密尔顿函数。上面的微分等式可以使用哈密尔顿函数重新表述为：

dvdtdhdt=∂Ep∂h=∂H∂h=−∂Ek∂v=−∂H∂vdvdt=∂Ep∂h=∂H∂hdhdt=−∂Ek∂v=−∂H∂v

上面即是哈密尔顿等式。

在系统的演化过程中（物体降落），哈密尔顿函数的值是不变的：

dHdt=∂H∂hdhdt+∂H∂vdvdt=−∂H∂h∂H∂v+∂H∂v∂H∂h=0dHdt=∂H∂hdhdt+∂H∂vdvdt=−∂H∂h∂H∂v+∂H∂v∂H∂h=0

可以理解为物体增加的动能等于减少的势能，即能量守恒。

哈密尔顿等式中的 hh 和 vv 是联动且一一对应的，而 (h,v)(h,v) 组成的空间称为相空间（phase space）。一个物体的下落过程在 (h,v)(h,v) 相空间中表现为一个等值曲线（哈密尔顿函数值）。不同的初始设定 (h0,v0)(h0,v0) 确定了不同的等值曲线（当然对应不同的哈密尔顿函数值）。

动力系统与概率分布

上面的动力学和概率分布有什么关系呢？如果用相空间上的位置 hh 表示目标分布 p(z)p(z) 的变量 zz（后面的位置都用 zz 表示），希望可以设计一个合适的动力系统来遍历相空间，使得遍历（采样）得到的点 (z0,v0),(z1,v1),…,(zn,vn)(z0,v0),(z1,v1),…,(zn,vn) 中的 zizi 符合目标分布。

下面来看设计思路。

首先，（任何）概率分布 p(z)p(z) 都可以重新表示为 1Zpexp(−(−log(p(z))))1Zpexp(−(−log(p(z))))。设 E(z)=−log(p(z))E(z)=−log(p(z))，则 p(z)=1Zpexp(−E(z))p(z)=1Zpexp(−E(z))，其中 E(z)E(z) 可以理解为势能。

接下来引入动能 K(v)=v22K(v)=v22，和对应的概率分布 p(v)=1Zkexp(−K(v))p(v)=1Zkexp(−K(v))。

设哈密尔顿函数是 H(z,v)=E(z)+K(v)H(z,v)=E(z)+K(v)，则由 zz 和 vv 组成的联合分布可以表示为：

p(z,v)=p(z)p(v)=1ZHexp(−(E(z)+K(v)))=1ZHexp(−H(z,v)).p(z,v)=p(z)p(v)=1ZHexp(−(E(z)+K(v)))=1ZHexp(−H(z,v)).

如果能以符合 p(z,v)p(z,v) 分布的方式对相空间 (z,v)(z,v) 遍历（采样），那得到的 zizi 将符合 zz 的边际分布，也是目标分布 p(z)p(z)。

采样

对 p(z,v)p(z,v) 的采样可以借鉴 Metropolis 方法：

选取初始样本 (zi,vi)(zi,vi)
执行提议过程（要求对称）得到 (z∗,v∗)(z∗,v∗)
1. 以 min(1,p(z∗,v∗)p(zi,vi))min(1,p(z∗,v∗)p(zi,vi)) 的概率接受 (zi+1,vi+1)=(z∗,v∗)(zi+1,vi+1)=(z∗,v∗)
2. 否则 (zi+1,vi+1)=(zi,vi)(zi+1,vi+1)=(zi,vi)
重复第 2 步

HMC 与 Metropolis 所不同的就是对新样本的提议过程。HMC 通过对动力系统的模拟演化来提议新样本，即以 (zi,vi)(zi,vi) 为初始状态，按照哈密尔顿等式，通过固定时间（固定步数）的迭代得到 (z∗,v∗)(z∗,v∗)。理论上，哈密尔顿等式保证了 HH 是恒定的，p(z∗,v∗)=p(zi,vi)p(z∗,v∗)=p(zi,vi)，新样本必然会被接受。也正是这个特性保证了 HMC 较高的接受率。但在实际的计算过程中是通过离散的方法模拟连续的过程，必然会出现误差，所以依然使用 Metropolis 方法来判断是否接受新样本，以此来保证所有样本符合 p(z,v)p(z,v) 分布。

对哈密尔顿等式的计算通常采样“青蛙跳（leapfrog）”的方法模拟：

vˆ(t+ϵ/2)zˆ(t+ϵ/2)vˆ(t+ϵ)=vˆ(t)+ϵ2∂E∂z(zˆ(t))=zˆ(t)−ϵ∂K∂v(vˆ(t+ϵ/2))=zˆ(t)−ϵvˆ(t+ϵ/2)=vˆ(t+ϵ/2)+ϵ2∂E∂z(zˆ(t+ϵ))v^(t+ϵ/2)=v^(t)+ϵ2∂E∂z(z^(t))z^(t+ϵ/2)=z^(t)−ϵ∂K∂v(v^(t+ϵ/2))=z^(t)−ϵv^(t+ϵ/2)v^(t+ϵ)=v^(t+ϵ/2)+ϵ2∂E∂z(z^(t+ϵ))

jun add::这里的推导是根据一阶泰勒展开和上文中的dv/dt = dH/dh （对h的偏导，这里不好打格式）

，其中 ϵϵ 表示步幅系数。上面是一个完整的步骤，而模拟过程通常是循环固定的次数（LL，可调整的参数）。这个步骤简单解释起来是 vv 先前进半步（ϵ2ϵ2），然后 zz 前进一步（ϵϵ），最后 vv 再前进半步（ϵ2ϵ2）。在循环多次的情况下，上一次最后对 vv 的调整可以和下一次开头对 vv 的调整合并为一步。

Metropolis 方法要求提议的过程的对称的，这个可以通过随机采用 ϵϵ 或者 −ϵ−ϵ 来保证，即在相空间中是正向前进还是反向前进。“青蛙跳”的过程保证，从 (zi,vi)(zi,vi) 正向前进到 (z∗,v∗)(z∗,v∗) 后，反向经过相同的步数可以准确回到 (zi,vi)(zi,vi)。（满足 detailed balance 的证明过程可以参考 PRML 11.5.2）

遍历

上面的过程保证了较高的接受率，但是提议过程并不完整。因为给定初始的 (z0,v0)(z0,v0) 后，后续的样本都保持 H(zi,vi)H(zi,vi) 恒定，也就是 p(zi,vi)p(zi,vi) 是固定的。这样显然不能遍历整个的 p(v,v)p(v,v) 分布。

解决办法是，在下次执行哈密尔顿模拟过程之前，从条件分布 p(v′i∣zi)p(vi′∣zi) 中采样出一个新的 v′ivi′，以 (zi,v′i)(zi,vi′) 作为下次模拟过程的初始点。这个过程实际是选择了一个不同 HH 值，也就选择了一个不同的等值曲线。

像 Gibbs 方法一样，从条件分布中采样并没有破坏 p(z,v)p(z,v) 分布。而由于 p(z,v)p(z,v) 中 zz 和 vv 是相互独立的，p(v∣z)=p(v)p(v∣z)=p(v)，所以可以直接从 p(v)p(v) 采样。实际上根据上面对动能 K(v)K(v) 的定义，可以直接从标准的高斯分布中采样 Normal(0,1)Normal(0,1)。

所以总结起来，HMC 的提议过程分两步：

从 p(v∣z)=p(v)p(v∣z)=p(v) 中采样出 v′ivi′
与上一次的 zizi 组成新的初始点 (zi,v′i)(zi,vi′)，然后运行一定次数的“青蛙跳”，得到提议的样本 (z∗,v∗)(z∗,v∗)

有了 (z∗,v∗)(z∗,v∗) 接下再执行依据 min(1,⋯)min(1,⋯) 概率的选择过程。

上面提议过程的步骤里，一个是从条件分布里采样，另一个是 Metroplis 过程，都没有改变 p(z,v)p(z,v) 分布。虽然这可以理解为依据上面的步骤得出的样本符合目标分布，但是如果能够证明这两步作为一个整体满足 detailed balance 条件，就能更好的理解这个方法。以后会跟进分析。

例子

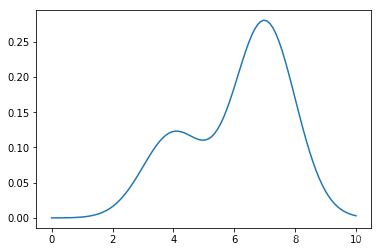
例子中的目标分布是一个高斯混合分布，中心点分别在 4 和 7，权重分别是 0.3 和 0.7。例子使用 PyTorch 实现，因为 PyTorch 提供了比较方便的计算梯度的方法。

完整的实现在 Hamiltonian-Monte-Carlo-import.ipynb 文件中，下面只列出了关键的步骤。

In [4]:

%%capture
%run Hamiltonian-Monte-Carlo-import.ipynb

定义目标概率分布：

In [2]:

def ptilde(x):
    return 0.3 * normpdf(x, mean=torch.tensor(4.0), scale=torch.tensor(1.0)) + 0.7 * normpdf(x, mean=torch.tensor(7.0), scale=torch.tensor(1.0))

下面看一下目标分布的密度函数曲线：

In [5]:

x = th.tensor(np.linspace(0, 10, num=100))
y = x.clone().apply_(ptilde)
plt.plot(np.array(x), np.array(y))

Out[5]:

[<matplotlib.lines.Line2D at 0x1159108d0>]

在引入动能之后，p(z,v)p(z,v) 的分布的等值曲线是这样的：

In [11]:

levels = np.arange(0,0.3,0.015)
contour(xx, yy, zs, levels=levels)

Out[11]:

<matplotlib.contour.QuadContourSet at 0x11563aa90>

右边紧密排列的圆是高密度区域。

然后定义在 p(z,v)p(z,v) 中采样的过程。

首先是青蛙跳的步骤。这里已经把中间步骤里前后两次对 vv 的半步前进合并成一步前进：

In [7]:

def leapfrog2(z, r, e=torch.tensor(0.001), L=100):
    if randint(1,2) == 1:
        e = -e
    z.requires_grad_(True)
    E = -torch.log(ptilde(z))
    E.backward()
    rhalf = r - 0.5 * e * z.grad
    rnext = rhalf
    znext = z

    for _ in range(L):
        with torch.no_grad():
            znext = znext + e * rnext
        znext.requires_grad_(True)
        E2 = -torch.log(ptilde(znext))
        E2.backward()
        with torch.no_grad():
            rnext = rnext - e * znext.grad

    with torch.no_grad():
        rnext = rnext + 0.5 * e * znext.grad

    return znext, rnext

然后是采样步骤：

In [8]:

def hmc2():
    n = 5000
    zs = []
    rs = []
    z0 = torch.tensor(4.0)
    for _ in range(n):
        r0 = torch.randn(1)
        zn, rn = leapfrog2(z0, r0, e=torch.tensor(0.15), L=20)
        nH = Hamilton(zn, rn)
        oH = Hamilton(z0, r0)
        if random.random() <= torch.exp(nH - oH):
            z0 = zn
        zs.append(z0.item())

    _ = hist(zs, bins=150)

采样结果，z 的直方图：

In [9]:

hmc2()

大致符合目标分布。下面跟其他实现方式比较一下。

首先是 Metropolis 方法：

In [12]:

metropolis()

然后是 PyMC3 提供的 HMC 方法：

In [13]:

pymc3_hmc()

100%|██████████| 5500/5500 [00:02<00:00, 2058.43it/s]

可以看到上面实现的 HMC 方法还是基本得到了正确的分布。

讨论

但是 HMC 引入额外的维度（参数，也就是动能）的意义是什么，为什么它能提高参数空间的探索效率？

下面先看一下连续的几次采样过程，包括青蛙跳的轨迹（下面 Traj 类的第二个参数是初始的 zz 值）：

In [16]:

%%capture
fig, ax = plt.subplots()
levels = np.arange(0,0.3,0.015)
ax.contour(xx, yy, zs, levels=levels)
traj = Traj(ax, 4.0)
anim = FuncAnimation(fig, traj, frames=np.arange(200), init_func=traj.init, interval=200, blit=True)

In [17]:

anim

Out[17]:

首先可以看出，青蛙跳的轨迹确实是沿着等值密度线前进。另外，在密度较高的地方，前进的步幅较小。还有，在右面密度最高的区域里，这些等值线与左边区域没有联通，所以落在这些圆上的点在青蛙跳之后依然会留在附近。这些都保证了 p(z)p(z) 大的地方得到更多的样本。

回到上面额外维度的问题。引入额外维度的意义在于可以实现飞跃，即不必受限于原有空间的沟沟坎坎而可以轻松的从 A 地到 B 地。如果跟飞机比的话，地上的火车可以认为是在二维的空间中前行。而有了飞机之后其实是增加了一个维度，可以不再受地面上各种条件的限制，可以实现（在地面看来）快速无痕迹的从 A 地到 B 地。

结合到上面的例子可以看出，如果初始点是在 p(z)p(z) 较低的地方，HMC 会以较大的步幅前进，快速的离开。

另外，哈密尔顿等式的应用保证了 HH 基本恒定，新提议的样本会以较高的概率被接受。

遗留的问题是，提议过程的两个步骤（条件分布采样和青蛙跳+Metropolis过程）作为一个整体是如何满足 detailed balance 条件的。这个问题以后会继续分析。

转载：Hamiltonian-Monte-Carlo