资源来自GitHub-算法导论第三版解析
第一章 算法基础
2.1 插入排序
2.1-1 以2-2为模型,说明INSERTION-SORT在数组A=<31,41,59,26,41,58>上的执行过程。
2.1-2 重写过程INSERTION-SORT,使之按非升序(而不是非降序)排序。
for j = 2 to A.length key = A[j] i = j - 1 while i > 0 and A[i] < key A[i + 1] = A[i] i = i - 1 A[i + 1] = key
2.1-3 考虑以下查找问题:
输入:n个数的一个序列A=<>和一个值v。
输出:下标i使得v=A[i]或者当v不在A中出现时,v为特殊值NIL。
写出线性查找的伪代码,它扫描整个序列来查找v。使得一个循环不变式来证明你的算法是正确的。确保你的循环不等式满足三条必要的性质。
LINEAR-SEARCH(A, v) for i = 1 to A.length if A[i] == v return i return NIL
2.1-4 考虑把两个n位二进制整数加起来的问题,这两个整数分别存储在两个n元数组A和B中。这两个整数的和应该按二进制形式存储在一个(n + 1)元数组C中。请给出该问题的形式化描述,并写出伪代码。
ADD-BINARY(A, B) C = new integer[A.length + 1] carry = 0 for i = 1 to A.length C[i] = (A[i] + B[i] + carry) % 2 // remainder carry = (A[i] + B[i] + carry) / 2 // quotient C[i] = carry return C
2.2 分析算法
2.2-1 用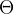 记号表示函数
记号表示函数 。
。
LaTex表达式:
$\Theta(n^3)$.
2.2-2 考虑排序存储在数组A中的n个数:首先找出A中的最小元素并将其与A[1]中的元素进行交换。接着,找出A中的次最小元素并将其与A[2]中的元素进行交换。对A中前n-1个元素按该方式继续。该算法称为选择算法,写出其伪代码。该算法维持的循环不变式是什么?为什么它只需要对前n-1个元素,而不是对所有的n个元素运行?用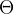 记号给出线性查找的平均情况和最坏情况运行时间。证明你的答案。
记号给出线性查找的平均情况和最坏情况运行时间。证明你的答案。
SELECTION-SORT(A) n = A.length for j = 1 to n - 1 smallest = j for i = j + 1 to n if A[i] < A[smallest] smallest = i exchange A[j] with A[smallest]平均时间/最坏时间:
2.2-3 再次考虑线性查找问题(参见练习2.1-3)。假定要查找的元素等可能地为数组中的任意元素,平均需要检查输入序列的多少元素?最坏情况又如何呢?用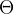 记号给出线性查找的平均情况和最坏情况运行时间。证明你的答案。
记号给出线性查找的平均情况和最坏情况运行时间。证明你的答案。
如果该元素存在于序列中,在平均情况下,在找到该元素之前可能会检查一半的元素。
在最坏的情况下,所有这些都将被检查。也就是说,检查平均情况,
检查最坏情况。
它们都是。
2.2-4 我们可以如何修改几乎任意算法来使之具有良好的最好情况运行时间?
修改算法,使其测试输入是否满足某些特殊情况条件,如果满足,则输出预先计算的答案。
最佳情况下的运行时间通常不是衡量算法的好方法。
2.3 设计算法
2.3-1 使用图2-4作为模型,说明归并排序在数组A=<3,41,52,26,38,57,9,49>上的操作。
2.3-2 重写过程MERGE,使之不使用哨兵,而是一旦数组L或R的所有元素均被复制回A就立刻停止,然后把另一个数组的剩余部分复制回A。
MERGE(A, p, q, r) n[1] = q - p + 1 n[2] = r - q let L[1..n[1]] and R[1..n[2]] be new arrays for i = 1 to n[1] L[i] = A[p + i - 1] for j = 1 to n[2] R[j] = A[q + j] i = 1 j = 1 for k = p to r if i > n[1] A[k] = R[j] j = j + 1 else if j > n[2] A[k] = L[i] i = i + 1 else if L[i] ≤ R[j] A[k] = L[i] i = i + 1 else A[k] = R[j] j = j + 1
2.3-3 使用数学归纳法证明:当n刚好是2的幂时,以下递归式的解是 。
。

2.3-4 我们可以把插入排序表示为如下的一个递归过程。为了排序A[1..n],我们递归地排序A[1..n-1],然后把A[n]插入已排序的数组A[1..n-1]。为插入排序的这个递归版本的最坏情况运行时间写一个递归式。
2.3-5 回顾查找问题(参见练习2.1-3),注意到,如果序列A已排好序,就可以将该序列的中点与v进行比较。根据比较的结果,原序列中有一半就可以不用再进一步的考虑了。二分查找算法重复这个过程,每次都将序列剩余部分的规模减半。为二分查找写出迭代或递归的伪代码。证明:二分查找的最坏情况运行时间为 。
。
ITERATIVE-BINARY-SEARCH(A, v, low, high) while low ≤ high mid = floor((low + high) / 2) if v == A[mid] return mid else if v > A[mid] low = mid + 1 else high = mid - 1 return NILRECURSIVE-BINARY-SEARCH(A, v, low, high) if low > high return NIL mid = floor((low + high) / 2) if v == A[mid] return mid else if v > A[mid] return RECURSIVE-BINARY-SEARCH(A, v, mid + 1, high) else return RECURSIVE-BINARY-SEARCH(A, v, low, mid - 1)当范围为空时,两个过程都不成功地终止搜索。
,如果找到值
,则终止它。
基于与搜索范围中中间元素的比较,继续搜索,范围减半。
因此,这些过程的递归式是,其解是
。
2.3-6 注意到2.1节中的过程INSERTION-SORT的第5~7行的while循环采用一种线性查找来(反向)扫描已排好序的子数组A[1..j-1]。我们可以使用二分查找(参见练习2.3-5)来把插入排序的最坏情况总运行时间改进到 吗?
吗?
过程insert - sort的第5-7行while循环向后扫描排序数组
为A[j]找到合适的位置。问题是,循环不仅为
搜索合适的位置,而且还将比
大的每个数组元素向右移动一个位置(第6行)。这些移动可能需要
时间,当
前面的所有j - 1个元素都大于
时,就会发生这种情况。
我们可以使用二分搜索将搜索的运行时间提高到,但是二分搜索对移动元素的运行时间没有影响。
因此,单靠二分查找无法将insert - sort的最坏情况运行时间提高到。
2.3-7 描述一个运行时间为 的算法,给定n个整数的集合S和另一个整数x,该算法能确定S中是否存在两个其和刚好为x的元素。
的算法,给定n个整数的集合S和另一个整数x,该算法能确定S中是否存在两个其和刚好为x的元素。
算法步骤:
- 对集合
进行排序;
- 假设
,设集合
是包含所有
元素的集合,并且
;
- 对集合
进行排序;
- 合并集合
和
;
中存在两个元素,当且仅当相同的值出现在合并输出的连续位置时,其和正好为
。
思考题
2-1 (在归并排序中对小数组采用插入排序)虽然归并排序的最坏情况运行时间为 ,而插入排序的最坏情况运行时间为
,而插入排序的最坏情况运行时间为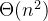 ,但是插入排序中的常量因子可能使得它在n较小时,在许多机器上实际运行得更快。因此,在归并排序中当子问题变得足够小时,采用插入排序来使递归的叶变粗是有意义的。考虑对归并排序的一种修改,其中使用插入排序来排序长度为k的n/k个子表,然后使用标准的合并机制来合并这些子表,这里k是一个待定的值。
,但是插入排序中的常量因子可能使得它在n较小时,在许多机器上实际运行得更快。因此,在归并排序中当子问题变得足够小时,采用插入排序来使递归的叶变粗是有意义的。考虑对归并排序的一种修改,其中使用插入排序来排序长度为k的n/k个子表,然后使用标准的合并机制来合并这些子表,这里k是一个待定的值。
a.证明:插入排序最坏情况可以在时间内排序每个长度为k的n/k个子表。
b.表明在最坏情况下如何在时间内合并这些子表。
c.假定修改后的算法的最坏情况运行时间为,要使修改后的算法与标准的归并排序具有相同的运行时间,作为n的一个函数,借助
记号,k的最大值是什么?
d.在实践中,我们应该如何选择k?
a.在最坏的情况下,每个k元素列表的插入排序花费
时间。因此,排序
个包含
个元素的列表,每个列表需要
最坏情况时间。
b.仅仅扩展2-list merge来一次合并所有的list就需要
的时间(n来自于将每个元素复制一次到结果列表中,
来自于在每一步检查
个list来选择结果列表的下一个项目)。为了实现
时间的合并,我们成对地合并列表,然后成对地合并结果列表,以此类推,直到只剩下一个列表。两两合并需要在每个级别上做
的工作,因为我们仍然要处理n个元素,即使它们被划分在子列表中。从
个列表(每个列表有
个元素)开始,到1个列表(有n个元素)结束,层级数为
。因此,合并的总运行时间是
.
c.当
时,改进算法的渐近运行时间与标准归并排序相同。满足此条件的
作为
的函数的最大渐近值为
。
明白为什么,首先观察到不能超过
(也就是说,它不可能有比
高阶的项),否则左手表达式不会是
(因为它有一个比
高阶的项)。所以我们需要做的是验证
这件事,
我们可以将
插入:
得到:
保留高阶项和省略常数项系数,等于
。
d.在实践中,
应该是使插入排序比归并排序更快的最大列表长度。
2-2 (冒泡排序的正确性)冒泡排序是一种流行但低效的排序算法,它的作用是反复交换相邻的未按次序排序的元素。

a.假设表示BUBBLESORT(A)的输出。为了证明BUBBLESORT正确,我们必须证明它将终止并且有:
![]()
其中n=A.length。为了证明BUBBLESORT确实完成了排序,我们还需要证明什么?
下面两部分将证明不等式(2.3)。
b.为第2~4行的for循环精确地说明一个循环不等式,并证明该循环不变式成立。你的证明应该使用本章中给出的循环不变式证明的结构。
c.使用(b)部分证明的循环不变式的终止条件,为第1~4行的for循环说明一个循环不变式,该不变式将你能证明不等式(2.3)。你的证明应该使用本章中给出的循环不变式证明的结构。
d.冒泡排序的最坏情况运行时间是多少?与插入排序的运行时间相比,其性能如何?
a.我们需要证明A'中的元素构成了A的元素的排列
b.循环不变量:在第2-4行for循环的每次迭代开始时,
,在循环开始时子数组
是
中值的排列。
初始化:初始,子数组
由单个元素
组成。循环不变式显然成立。
维护:对于给定的值,考虑一次迭代。依据循环不变式,
是
中的最小值。第 3 - 4 行在
小于
时交换
和
,于是此后
将成为
中的最小值。由于对
子数组的唯一变动是这种可能的交换,并且子数组
是循环开始时
中值的一个排列,所以我们可以看出
是循环开始时
中值的一个排列。将
递减以用于下一次迭代可维持不变式。
终止:当到达
时循环终止。通过循环不变量的语句,
是在循环开始时
中的值的排列。
c.循环不变量:在1 - 4行
循环的每次迭代开始时,子数组
由原来在
中的
最小值组成。按顺序排列,
由原来在
中剩余的
组成。
初始化:在循环第一次迭代之前,
。子数组
为空,因此循环不变式成立。
维护:考虑对给定值
进行迭代。通过循环不变式,
由
中的
最小值组成,按顺序排列。(b)部分显示,在执行了2-4行的
循环后,
是
中最小的值,所以
现在是
最小的值原来在
,按顺序排列。此外,由于第2-4行中的
循环将
,子数组
由原来在
中剩余的
组成。
终止:第1 - 4行的
循环在
时终止,因此
。通过循环不变式的语句,
是子数组
,它由原来在
中的
最小值组成,按顺序排列。剩下的元素必须是
中的最大值,并且在
中。因此,整个数组
已排序。
注释:在第二版中,第1-4行的
循环的上界为
。外部
循环的最后一次迭代将不会导致第1 - 4行内部
循环的迭代,但是termination参数将简化
将是整个数组
,根据循环不变式,它是排序的。
d.运行时间取决于第2-4行for循环的迭代次数,对于给定的
值,循环进行
次迭代(
的取值是
。因此,迭代的总次数是:
因此,在所有情况下,冒泡排序的运行时间为
。最坏情况下的运行时间与插入排序相同。
2-3 (霍纳(Horner)规则的正确性)给定系数  和x的值,代码片段实现了用于求值多项式的霍纳规则。
和x的值,代码片段实现了用于求值多项式的霍纳规则。

![]()
a.借助记号,实现霍纳规则的以上代码片段的运行时间是多少?
b.编写伪代码来实现朴素的多项式求值算法,该算法从头开始计算多项式的每个项。该算法的运行时间是多少?与霍纳规则相比,其性能如何?
c.考虑以下循环不变式:
在第2~3行for循环每次迭代的开始有
把没有项的和式解释为等于0.遵照本章中给出的循环不变式证明的结构,使用该循环不变式来证明终止时有。
d.最后证明上面给出的代码片段将正确地求由系数刻画的多项式的值。
a.
b.由于嵌套循环,运行时间为
。它显然更慢。
NAIVE-HORNER() y = 0 for k = 0 to n temp = 1 for i = 1 to k temp = temp * x y = y + a[i] * m
c. 初始化:这是相当微不足道的,因为求和没有项意味着
。
维护:通过使用循环不变量,在
迭代结束后,我们有
终止:循环在
处终止。如果代入,
d.循环的不变量是一个等于给定系数的多项式的和。
2-4 (逆序对)假设![A[1,\dots,n]](https://latex.csdn.net/eq?A%5B1%2C%5Cdots%2Cn%5D) 是一个有
是一个有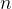 个不同数的数组。若
个不同数的数组。若 且
且![A[i]>A[j]](https://latex.csdn.net/eq?A%5Bi%5D%3EA%5Bj%5D) ,则对偶
,则对偶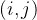 称为
称为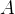 的一个逆序对(inversion)。
的一个逆序对(inversion)。
a.列出数组的5个逆序对。
b.由集合中的元素构成的什么数组具有对多的逆序对?它有多少逆序对?
c.插入排序的运行时间与输入数组中逆序对的数量之间是什么关系?证明你的回答。
d.给出一个确定在n个元素的任何排列中逆序对数量的算法,最坏情况需要时间。(提示:修改归并排序)
a.倒置(1、5),(2、5),(3、4),(3、5)(4、5)。(请记住,反转是由索引而不是数组中的值指定的。)
b.
中反转次数最多的数组是
。对于所有
,存在反转
。这种反转的次数是
。
c.假设数组
以反转
开始。则
和
。当第1-8行外部的
循环设置
时,从
开始的值仍然在
左边的某个地方。也就是说,它在
中,其中
,因此反转就变成了
。第5-7行
循环的一些迭代将
的位置向右移动。第8行最终将
放到该元素的左侧,从而消除了反转。因为第5行只移动大于
的元素,所以它只移动与反转相对应的元素。换句话说,第5-7行
循环的每次迭代对应于消除一次反转。
d.我们按照提示修改归并排序,在
时间内计算反转的次数。
首先,让我们将合并反转定义为在执行合并排序时的一种情况,其中
过程在复制
到
和
到
,在
中有
,在
中有
,使得
。考虑一个反转
,令
;
;,使得
,
。我们声称,如果我们要运行归并排序,只会有一个涉及
和
的归并反转。要了解原因,请观察数组元素改变位置的唯一方式是在
过程中。此外,由于
将
中的元素保持彼此之间相同的相对顺序,对于
也是如此,两个元素可以改变彼此之间相对顺序的唯一方法是较大的元素出现在
中,较小的元素出现在
中。因此,至少存在一个涉及
和
的合并反转。要查看是否只存在一个这样的合并反转,请观察在调用
(同时涉及
和
)之后,它们在相同的排序子数组中,因此在此后的任何给定调用中都将出现在
中或同时出现在
中。因此,我们证明了这一说法。
我们已经证明,每一个反转都意味着一个合并反转。事实上,反转和合并反转之间的对应关系是一对一的。假设我们有一个涉及值
和
的合并反转,其中
最初是
,
最初是
。因为我们有一个合并反转,
。由于
在
中,
在
中,因此
必须在包含
的子数组之前的子数组中。因此,
在
的初始位置
之前的位置
开始,因此
是一个反转。
在展示了反转和合并反转之间的一对一对应关系之后,我们就可以计算合并反转了。
考虑一个涉及
在
中的合并反转。设
是
中大于
的最小值。在合并过程中的某个时刻,
和
将是
和
中“暴露”的值,也就是说,我们将在
的第13行中拥有
和
。那时,将会有涉及
和
的合并反转,而这些
合并反转将是唯一涉及
的合并反转。因此,我们需要在
过程中检测
和
第一次暴露,并将当时的
的值添加到我们的合并反转总数中。
下面的伪代码以合并排序为模型,其工作方式与我们刚才描述的一样。它还对数组
进行排序。
COUNT-INVERSIONS(A, p, r)
inversions = 0
if p < r
q = floor((p + r) / 2)
inversions = inversions + COUNT-INVERSIONS(A, p, q)
inversions = inversions + COUNT-INVERSIONS(A, q + 1, r)
inversions = inversions + MERGE-INVERSIONS(A, p, q, r)
return inversionsMERGE-INVERSIONS(A, p, q, r)
n[1] = q - p + 1
n[2] = r - q
let L[1..n[1] + 1] and R[1..n[2] + 1] be new arrays
for i = 1 to n[1]
L[i] = A[p + i - 1]
for j = 1 to n[2]
R[j] = A[q + j]
L[n[1] + 1] = ∞
L[n[2] + 1] = ∞
i = 1
j = 1
inversions = 0
for k = p to r
if R[j] < L[i]
inversions = inversions + n[1] - i + 1
A[k] = R[j]
j = j + 1
else A[k] = L[i]
i = i + 1
return inversions初始调用是
.
在
中,每当在
数组中暴露了
并且暴露了一个大于
的值时,我们增加了
中剩余元素的个数。然后因为
被暴露了,
再也不会被暴露了。我们不必担心涉及
中的哨兵
的合并反转,因为
中的任何值都不会大于
。
由于我们只在每个过程调用和合并过程的最后一个
循环的每次迭代中添加了一定量的额外工作,因此上述伪代码的总运行时间与合并排序的运行时间相同:
。




























 1224
1224

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








