算法（五）图论

1. 基本定义及应用

1.1 无向图

无向图。G = (V, E)

• V =节点(或顶点)
• E =节点对之间的边。
• 捕获对象之间的成对关系。
• 图形大小参数:n = |V|， m = |E|。
  

1.2 术语(无向图)

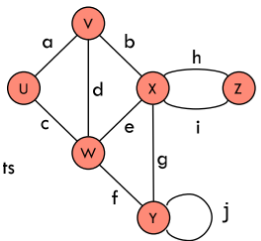
• 边连接端点endpoints；例如，W和Y代表边f
• 边与端点关联incident；例如，a、d和b关联在V上
• 相邻adjacent的顶点是连接的；例如，U和V是相邻的
• 度数degree是顶点上的边数；例如，X有5个degree，y有四个degree
• 平行的边共享相同的端点；h和i是平行的
• 自循环self-loop只有一个端点；例如，j是一个自循环
• 简单的图形没有平行或自循环
  

1.3 路径和连接

无向图G = (V, E)中的一条路径是节点v1, v2，…，vk-1, vk的序列P，其性质是每对连续的vi, vi+1都由E中的一条边连接。
如果所有节点都是不同的，那么路径是简单的。
如果对于每一对节点u和v, u和v之间都有一条路径，则无向图是连通的。

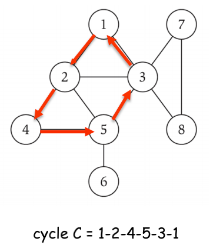
1.4 周期cycles

定义：循环的路径是v1, v2，…，vk-1, vk，其中v1 = vk, k > 2，第一个k-1节点都是不同的。

1.5 树tree

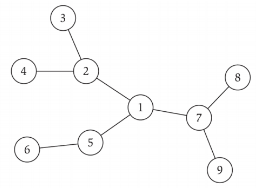
定义：如果无向图是连通的且不包含循环，那么它就是树。
定理：设G是n个节点上的无向图。下面的任何两个陈述都暗示了第三个。
G是连接的 / G不包含一个循环 / G有n-1条边

2 图的数据结构 Graph Data Structures

2.1 边表结构Edge List Structure

顶点序列保存

• 顶点序列
• 顶点对象跟踪其在序列中的位置

边的序列

• 序列的边缘
• 边缘对象保持其在序列中的位置
• 边缘对象指向它连接的两个顶点
  

2.2 邻接表 Adjacency list

另外，每个顶点都保持一个关联在其上的边序列
边缘对象始终参照它们在端点关联序列中的位置

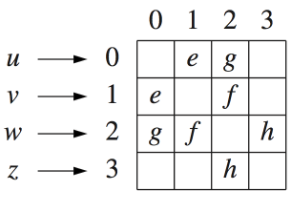
2.3 邻接矩阵结构

顶点数组引出了每个顶点从0到n-1的索引
2维数组邻接矩阵

• 为相邻的顶点引用edge对象
• 不相邻的顶点为空
  

2.4 渐近性能 Asymptotic performance

3 图的遍历 Graph Traversal

我们希望在图上执行的一种基本算法操作是遍历图的边和顶点。遍历是一种通过检查图的所有顶点和边来探索图的系统过程。如果在线性时间内访问所有的顶点和边，那么遍历是有效的:O(n+m)，其中n=顶点的数量，m=边的数量。

3.1 广度优先搜索（BFS）

从s向外探索所有可能的方向，每次添加一个“层”节点。
定理。对于每一个i, Li由所有距离s为i的节点组成。在某一层中出现了从s到t的路径。

• L0 = {s}。
• L1 = L0的所有邻域。
• L2 =不属于L0或L1的所有节点，并且与L1中的某个节点有一条边。
• Li+1 =不属于前一层的所有节点，并且在Li中有一个节点的边。

案例

如果图是由邻接表表示法给出的，上述BFS实现的运行时间为O(m + n）

最短路径

图G中两个节点u,v之间的最短路径，是连接u和v的边数最少的路径(如果存在的话)
最短路径问题:
输入:图G=(V,E)， V中的两个节点u, V
输出:u到v的最短路径的长度

3.2 深度优先搜索 Depth-First Search (DFS)

这个策略尝试在任何可能的情况下跟随传出的边到达尚未访问的顶点，如果“卡住”，则回溯。
如果一条边被用来发现一个新的顶点，我们称它为DFS edge，否则我们称它为back edge。

案例

时间复杂度 O(n+m)

割边

定义：在连通图中，如果边e的移除会断开图的连接，则称为“切边”
G = (V,E)为连通
G ’ = (V,E \ {E})未连接

3.3 DFS vs BFS

4. Bipartite Graphs 二分图

定义：无向图G = (V, E)是二部图，如果节点可以被涂成红色或蓝色，使得每条边都有一个红色和一个蓝色的末端。
应用：

• 稳定的婚姻:公司=红色，实习生=蓝色。
• 调度:机器=红色，工作=蓝色。
  

4.1 一式两份的图Bipartite Graphs

引理。设G为连通图，设L0，…，Lk为BFS从节点s开始生成的层。
(i) G没有边连接同一层的两个节点，G是二部图。
(ii) G的一条边连接同一层的两个节点，G包含一个奇长环(因此不是二部图)。

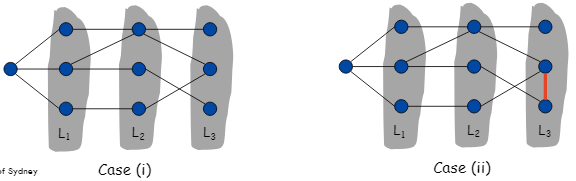
阻碍Bipartiteness
推论：当且仅当它不包含奇长环，图G是二部图。

5. 有向图的连通性

有向图G = (V, E)
-边(u, v)从节点u到节点v。

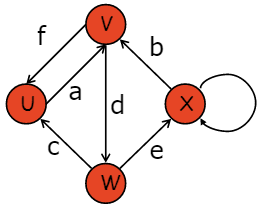
5.1术语(指示图)

边从尾到头，例如，W是c的尾，U是头
outer-degree 是顶点外的边数，例如，W的外度为2
in-degree 是进入顶点的边数，例如W的out度为1
parallel deges 共享尾和头，如右侧没有平行边
self-loop 有相同的头和尾，例如，X有一个自环
简单有向图没有平行或自循环，但允许有反平行的循环，如f和a

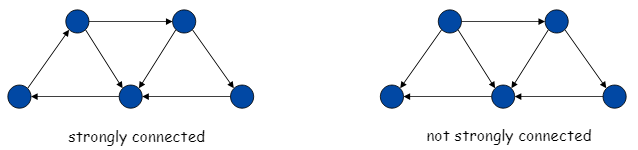
5.2 强连接strong connectivity

• 如果有一条从u到v的路径，也有一条从v到u的路径，那么节点u和v是mutually reachable的。
• 如果图中的每对节点都是mutually reachable的，则图是strong connectivity的。
• 可以确定G在O(m + n)时间内是否强连通。
  

6. DAGs和拓扑排序Topological Ordering

6.1 有向无环图 Directed Acyclic Graphs

DAG是一个不包含有向循环的有向图。
例:优先约束:边(vi, vj)意味着vi必须在vj之前。
有向图G = (V, E)的拓扑序是它的节点v1, v2，…，vn的顺序，所以对于每条边(vi, vj)我们都有i < j。

优先约束：Edge (vi, vj)意味着任务vi必须出现在vj之前。
如果G有拓扑顺序，那么G是一个DAG。
如果G是一个DAG，那么G有一个没有传入边的节点。
算法在O(n + m)时间内找到拓扑顺序。