Preface
由于能力有限,没有看和了解太多东西,这里只写了一些简单版的学习资料(仅仅是我见过的),有些言语颇显幼稚,可能还有些不完整,望大神不喜勿喷,欢迎补充。。。
Content
Definition:
孙子定理是中国古代求解一次同余式组(见同余)的方法。是数论中一个重要定理。又称中国剩余定理。 ——度娘
中国剩余定理称Chinese remainder theorem 简称CRT
Formulation:
举个一个简单的例子:
有1个数,除以7余2.除以8余4,除以9余3,这个数至少是多少?
解:除以7余2的数可以写成7n+2。
7n+2这样的数除以8余4,由于2除以8余2,所以要求7n除以8余2。
7n除以8余2,7除以8余7,要求n除以8余6(乘数之余等于余数之乘),则n最小取6。
所以满足“除以7余2,除以8余4”的最小的数是7×6+2=44,
所有满足“除以7余2,除以8余4”的数都可以写成44+56×m。
要求44+56×m除以9余3,由于44除以9余8,所以要求56×m除以9余4。(加数之余等于余数之加)
56×m除以9余4,由于56除以9余2,所以要求m除以9余2(乘数之余等于余数之乘),则m最小取2。
所以满足“除以7余2,除以8余4,除以9余3”的最小的数是44+56×2=156。
以上这个例子所解得方法是数学方法,在这里解释一下
乘数之余等于余数之乘:如果a%c=d,b%c=e,则ab%c=de%c (个人见解)
加数之余等于余数之加:如果a%c=d,b%c=e,则(a+b)%c=(d+e)%c.(同上)
若将这个问题形式化并推广到一般形式:
这里分为两个部分:
①设正整数
方程有整数解,并且在模
解为:
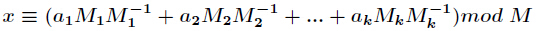
其中
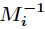 表示Mi%mi的逆元。
表示Mi%mi的逆元。
Code
long long Exgcd(long long a,long long b,long long &x,long long &y)
{
if (!b)
{
x=1;y=0;
return a;
}
long long d=Exgcd(b,a%b,x,y);
long long t=x;
x=y;
y=t-(a/b)*y;
return d;
}
long long CRT(long long a[],long long m[],int n)
{
long long M=1;
long long ans=0;
fo(i,1,n) M*=m[i];
fo(i,1,n)
{
long long x=0, y=0;
long long Mi=M/m[i];
Exgcd(Mi,m[i],x,y);
ans=(ans+Mi%M*x%M*a[i]%M+M)%M;
}
if(ans<0) ans+=M;
return ans;
} ②两两不互素的情况下:
为了方便起见,我们先来研究一下方程组中只有两个方程时候的解法。
对同余方程组
x = a1 (mod m1)
x = a2 (mod m2)
可以将它们转化为我们熟悉的形式,即
x - m1*y1 = a1
x - m2*y2 = a2(y1、y2为任意整数)
消去x得到
熟悉数论的人一眼就可看出该式可用扩展欧几里德算法求解y1、y2的特殊解,关于扩展欧几里得算法可以参考我的另一篇博客 扩展欧几里得
这样得出的ans就是gcd(a, b),x和y则是一组可行解。
有了扩展欧几里德算法我们现在可以来解
首先根据裴蜀定理判断解的存在性,
当gcd(m1, m2)不能整除(a2 - a1)时一定无解。
排除掉无解的情况后,先用扩展欧几里德算法解出
PS.裴蜀定理:
下面介绍一下:
裴蜀定理:对于方程
有整数解的充分必要条件是(n % gcd(a,b)== 0),即n能够被a和b的最大公约数整除,其实就是扩展的欧几里得定理。
所以对方程
还有一个定理:若
这样我们就可以求出方程的所有解了,但实际问题中,我们往往被要求去求最小整数解,其实可以将一个特解x做如此处理:t = b / gcd(a,b),x = (x % t + t) % t(防止x是负数作此处理),即得到最小整数解。
其实当方程组有两个方程的情况会解之后,对一般情况的解法也已经出来了
这种解法其实是最朴素意义上的遍历法,即从头开始解两个方程的公共解x’,解出来将这两个方程从方程组中删除,再加入一个新的方程x = x’(mod lcm(m1, m2))(lcm是最小公倍数)到方程组中去,重复以上步骤直到所有方程都被消去,最后得到的解x就是该公共解.
这里有一道例题:
Jzoj 3093. 【NOIP2012模拟11.7】合唱队形
其他人怎么对的我不清楚,反正我是用中国剩余定理。。
贴上代码:
#include <cstdio>
#include <iostream>
#include <cmath>/
#include <algorithm>
#define mo 1000000007
#define fo(i,a,b) for (int i=a;i<=b;i++)
using namespace std;
long long m[15],a[15];
int n;
long long Exgcd(long long a,long long b,long long &x,long long &y)
{
if (!b)
{
x=1;y=0;
return a;
}
long long d=Exgcd(b,a%b,x,y);
long long t=x;
x=y;
y=t-(a/b)*y;
return d;
}
long long CRT(long long a[],long long m[],int n)
{
long long M=1;
long long ans=0;
fo(i,1,n) M*=m[i];
fo(i,1,n)
{
long long x=0, y=0;
long long Mi=M/m[i];
Exgcd(Mi,m[i],x,y);
ans=(ans+Mi%M*x%M*a[i]%M+M)%M;
}
if(ans<0) ans+=M;
return ans;
}
int main()
{
freopen("data.in","r",stdin);
scanf("%d",&n);
fo(i,1,n)
{
if (i==1)
{
scanf("%lld%lld",&m[1],&a[1]);
continue;
}
scanf("%lld%lld",&m[i],&a[i]);
long long x=0,y=0;
long long c=a[i]-a[1],d=Exgcd(m[1],m[i],x,y);
if (c%d)
{
printf("-1\n");
return 0;
}
x*=(c/d);
x=((x%m[i])+m[i])%m[i];
a[1]=m[1]*x+a[1];
m[1]=m[1]/d*m[i];
a[1]=a[1]%m[1];
}
printf("%lld",a[1]);
}是不是看的有点懵(⊙﹏⊙)b,其实我也很懵逼。。。
这种东西得靠时间消化与吸收呀。。。
我怕我明天就忘了o(╯□╰)o
好了,就这样的吧,若有不足请包涵。
蒟蒻一枚。。
The End
鸣谢:
度娘
ACdreamers
豆











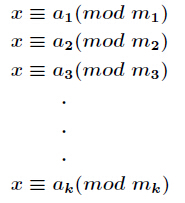

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








