正态分布（Normal Distribution）

原创已于 2023-05-04 10:02:00 修改 · 7.8k 阅读

·

11

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#学习 #python #人工智能

于 2023-05-03 16:27:51 首次发布

正态分布，又称为高斯分布，是一种连续概率分布，其特征由期望和方差决定。当期望为0，标准差为1时，形成标准正态分布。概率密度函数在期望值处达最大并关于其对称，而标准差影响分布的形状。样本方差是总体方差的无偏估计，方差衡量数据的离散程度。

正态分布（Normal Distribution），又名高斯分布（Gaussian Distribution），是一个常见的连续概率分布。

若随机变量X服从一个数学期望为 $\mu$ ，方差为 $\sigma^2$ 的正态分布，则可以记成：

$X\sim N(\mu,\sigma^2)$

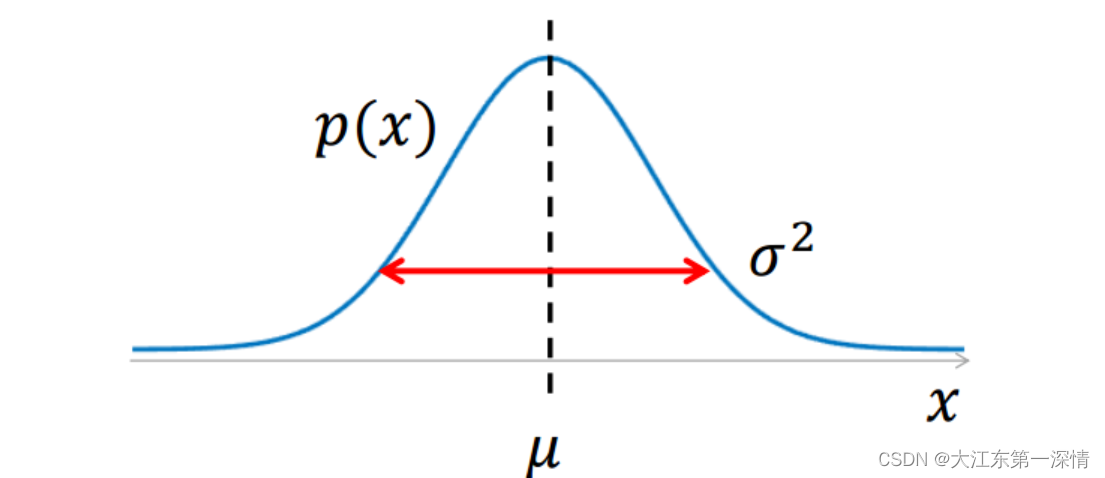
其概率密度函数为正态分布，期望值决定概率密度函数位置，标准差决定分布的幅度，当期望为0，标准差为1时的正态分布为标准正态分布。

$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

均值和总体方差计算方法：

$\mu =\frac{\sum_{i=1}^{n}{x_i}}{n}$

$\sigma^2=\frac{\sum_{i=1}^{n}{(x_i-\mu)^2}}{n}$

样本方差：

$\sigma^2=\frac{\sum_{i=1}^{n}{(x_i-\mu)^2}}{n-1}$

样本方差的期望是总体方差的一个无偏估计。

性质：

1. 概率密度在期望值 $\mu$ 处达到最大，且关于其对称；

2. 正态分布曲线完全决定于期望值和标准差；

3.概率密度积分为1；

4.标准差越大，概率密度函数图像越扁平，标准差越小，概率密度函数图像越陡峭集中。

均方误差：

方差：

$s^2 = \frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n}$

如果本篇文章解决了你的疑惑，请不要吝啬你的点赞哦，谢谢！

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。