应用回溯法算法解决哈密顿问题，时间空间复杂度分析

只因从未离去

已于 2023-11-19 21:48:46 修改

阅读量480

点赞数 1

文章标签：算法 c++ 开发语言数据结构

于 2023-11-19 21:45:02 首次发布

本文链接：https://blog.csdn.net/IKUNIKUNIKUNikun/article/details/134495087

版权

题目：

哈密顿回路的定义： G=(V,E)是一个图，若G中一条路径通过且仅通过每一个顶点一次，称这条路径为哈密顿路径。若G中一个回路通过且仅通过每一个顶点一次，称这个环为哈密顿回路。若一个图存在哈密顿回路，就称为哈密顿图。

答案代码示例：

#include<iostream>
#include<vector>
using namespace std;

void back(int g[15][15],int n,vector<int> &v,vector<vector<int>> &result,vector<bool> &visited){
	if(v.size()==n){
		if(g[v.back()][v.front()]==1&&g[v.front()][v.back()]==1){//需要回到起点才能构成哈密顿回路
			result.push_back(v);//将这一条回路放入结果中
			return;
		}
		return;
	}
	for(int i=0;i<n;i++){
		if(g[v.back()][i]==1&&!visited[i]){
			visited[i] = true;
			v.push_back(i);
			back(g,n,v,result,visited);
			v.pop_back();
			visited[i] = false;
		}
		else{
			continue;
		}
	}
	return;
}
int main(){
	int n=5;//节点数
	int g[15][15]={{0,1,0,1,0},{1,0,1,1,1},{0,1,0,1,1},{1,1,1,0,1},{0,1,1,1,0}};//测试数据(原题)
//	int g[15][15]={{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};//特殊值
//	int g[15][15]={{0,1,0,1,0},{1,0,1,1,1},{0,1,0,0,1},{1,1,0,0,1},{0,1,1,1,0}};//测试数据：输出：存在2条哈密顿回路:	1 2 3 5 4	1 4 5 3 2
//	int g[15][15]={{0,1,1,1,0},{1,0,1,0,1},{0,1,0,1,1},{1,0,1,0,1},{0,1,1,1,0}};//测试数据：输出：存在6条哈密顿回路:	1 2 3 5 4	1 2 5 3 4	1 3 2 5 4	1 3 4 5 2	1 4 3 5 2	1 4 5 3 2
	vector<int> v;//用来储存一条哈密顿回路
	vector<vector<int>> result;//用来储存所有的哈密顿回路
	vector<bool> visited(n,false);//用来储存已经走过的节点
	int begin=0;//设置起点
	v.push_back(begin);
	visited[begin]=true;
	back(g,n,v,result,visited);
	int answer=result.size();
	if(answer==0){
		cout<<"不存在哈密顿回路"<<endl;
	}
	else{
		cout<<"存在"<<answer<<"条哈密顿回路:" <<endl;
		for(auto a:result){
			for(auto b:a){
				cout<<b+1<<' ';
			}
			cout<<endl;
		}
	}
	
}

答案代码思路：

这段代码的思路是使用回溯法来寻找一个给定的图中是否存在哈密顿回路，即经过每个节点一次且仅一次的回路。回溯法是一种试探性的搜索方法，从一个起点开始，沿着可行的边逐步扩展路径，如果遇到死路，就回退到上一个节点，换一条边继续搜索，直到找到所有的回路或者遍历完所有的可能。

定义一个二维数组g[15][15]（15以上我的电脑内存就爆掉了），用来表示图的邻接矩阵，即g[i][j]表示节点i和节点j之间是否有边相连，0表示没有，1表示有。自身也是不能联通的，例如（1,1）（2,2）都为0.
定义一个一维数组visited[n]，用来记录已经访问过的节点，防止重复访问，visited[i]为true表示节点i已经访问过，false表示没有。
定义一个vector<int>v，用来存储一条哈密顿回路，即经过的节点的顺序，v的大小等于节点的个数n时，并可以回到起点，表示找到了一条回路。
定义一个二维vector<vector<int>> result，用来存储所有的哈密顿回路，每一行是一个向量v，表示一条回路。
回溯法也是十分暴力的一种办法，本质是将每一种可能在递归中访问出来；

为何叫回溯法，就是需要在一层递归结束后要将改变的部分属性复原，例如我代码中的这个部分：

if(g[v.back()][i]==1&&!visited[i]){
			visited[i] = true;
			v.push_back(i);
			back(g,n,v,result,visited);
			v.pop_back();
			visited[i] = false;
		}

在这层递归中我的visited与v都会复原，改变的只有更深层次的递归。

递归过程：

递归示意图：

递归示意图

这里我简单绘制了递归的过程，同样也可是使用代码实现相同的效果：

递归详细过程代码：

#include<iostream>
#include<vector>
using namespace std;

void back(int depth,int g[15][15],int n,vector<int> &v,vector<vector<int>> &result,vector<bool> &visited){
	if(v.size()==n){
		cout<<"	触底,判断是否可以回到起点：";
		if(g[v.back()][v.front()]==1&&g[v.front()][v.back()]==1){//需要回到起点才能构成哈密顿回路
			cout<<"可以，添加此结果，当前路线为：";
			for(auto b:v){
				cout<<b+1<<' ';
			}
			cout<<endl;
			result.push_back(v);//将这一条回路放入结果中
			return;
		}
		cout<<"不行，不添加此结果"<<endl;
		return;
	}
	for(int i=0;i<n;i++){
		cout<<"深度:"<<depth<<"	路径:";
		for(auto b:v){
			cout<<b+1<<' ';
		}
		cout<<"	";
		if(g[v.back()][i]==1){
			cout<<v.back()+1<<"与"<<i+1<<"之间有通路	";
			if(visited[i]){
				cout<<i+1<<"但已被访问过，跳过"<<endl;
			}
			else{
			cout<<i+1<<"未被访问过，进入递归"<<endl;
			visited[i] = true;
			v.push_back(i);
			back(++depth,g,n,v,result,visited);
			v.pop_back();
			depth--;
			visited[i] = false;
			}
		}
		else{
			cout<<v.back()+1<<"与"<<i+1<<"之间没有通路,跳过"<<endl;
			continue;
		}
	}
	return;
}
int main(){
	int n=5;//节点数
	int g[15][15]={{0,1,0,1,0},{1,0,1,1,1},{0,1,0,1,1},{1,1,1,0,1},{0,1,1,1,0}};//测试数据(原题)
	//	int g[15][15]={{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0}};//特殊值
	//	int g[15][15]={{0,1,0,1,0},{1,0,1,1,1},{0,1,0,0,1},{1,1,0,0,1},{0,1,1,1,0}};//测试数据：输出：存在2条哈密顿回路:	1 2 3 5 4	1 4 5 3 2
	//	int g[15][15]={{0,1,1,1,0},{1,0,1,0,1},{0,1,0,1,1},{1,0,1,0,1},{0,1,1,1,0}};//测试数据：输出：存在6条哈密顿回路:	1 2 3 5 4	1 2 5 3 4	1 3 2 5 4	1 3 4 5 2	1 4 3 5 2	1 4 5 3 2
	vector<int> v;//用来储存一条哈密顿回路
	vector<vector<int>> result;//用来储存所有的哈密顿回路
	vector<bool> visited(n,false);//用来储存已经走过的节点
	int begin=0;//设置起点
	v.push_back(begin);
	visited[begin]=true;
	int depth=1;
	back(depth,g,n,v,result,visited);
	int answer=result.size();
	if(answer==0){
		cout<<"不存在哈密顿回路"<<endl;
	}
	else{
		cout<<"存在"<<answer<<"条哈密顿回路:" <<endl;
		for(auto a:result){
			for(auto b:a){
				cout<<b+1<<' ';
			}
			cout<<endl;
		}
	}
	
}

代码结果：

得出的结果为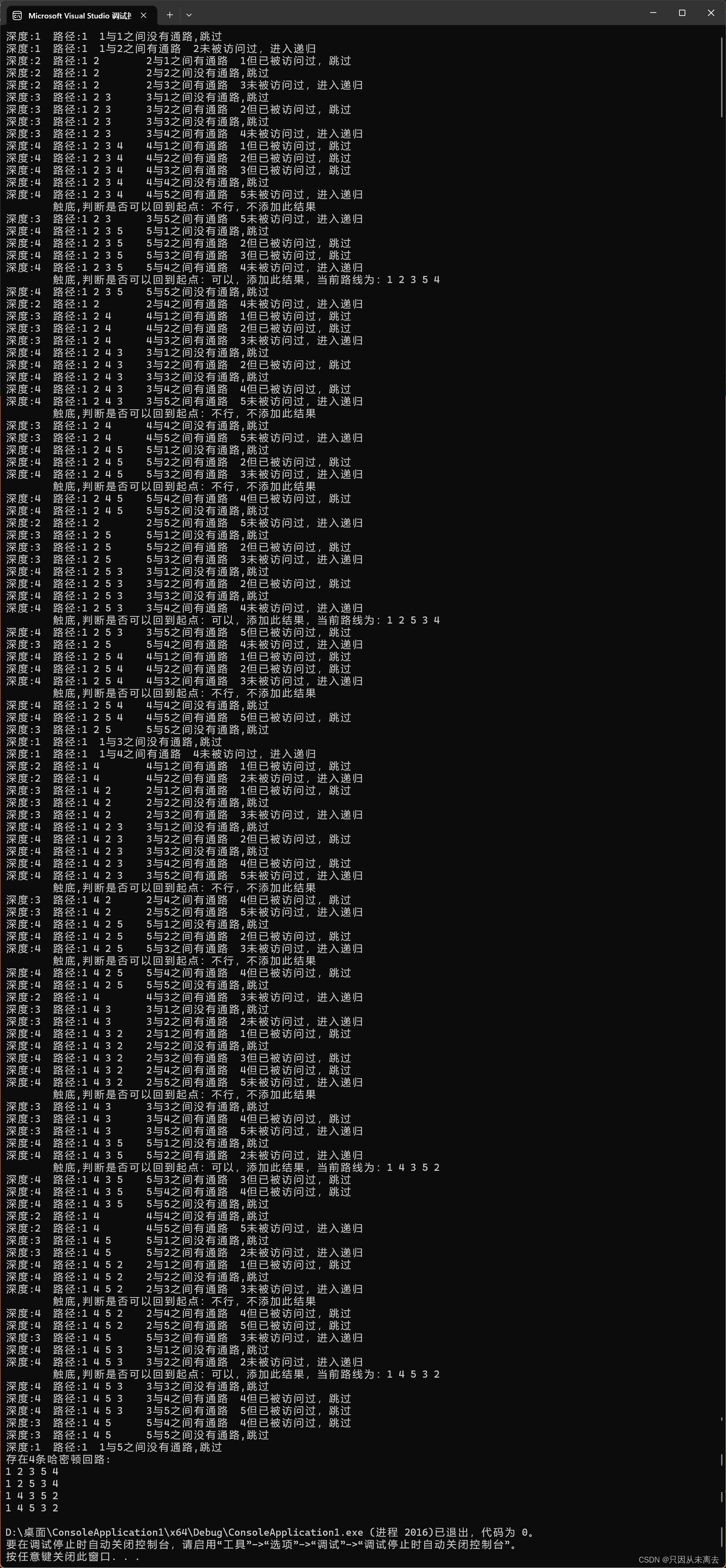：代码实现的递归过程

这里我们可以很清楚的看到递归的运算过程，希望能帮助大家理解

时间，空间复杂度分析：

数据：

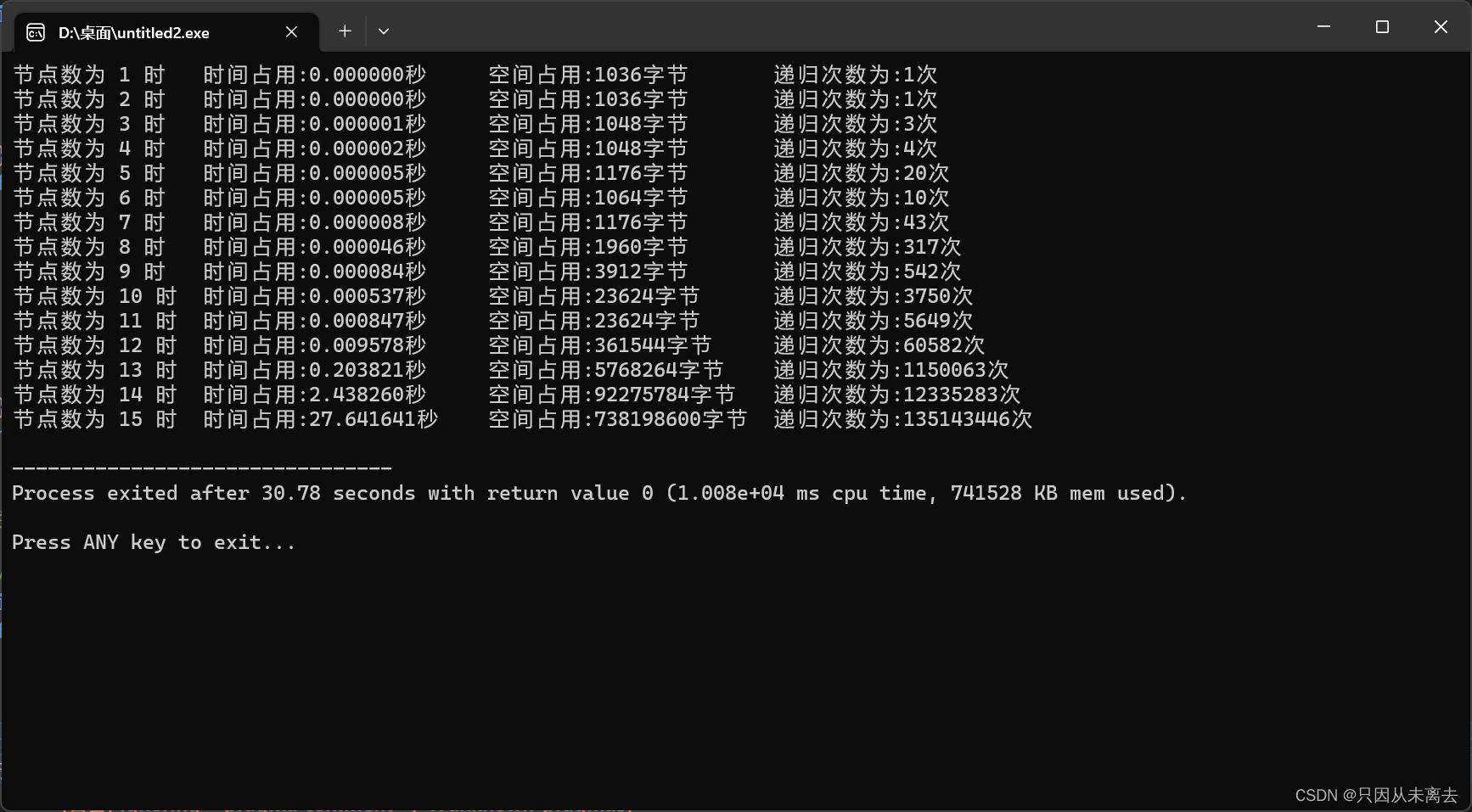
这边我们可以很清楚的看到这个复杂度已经不是指数级别的了，递归次数已经上亿次。

时间复杂度分析：

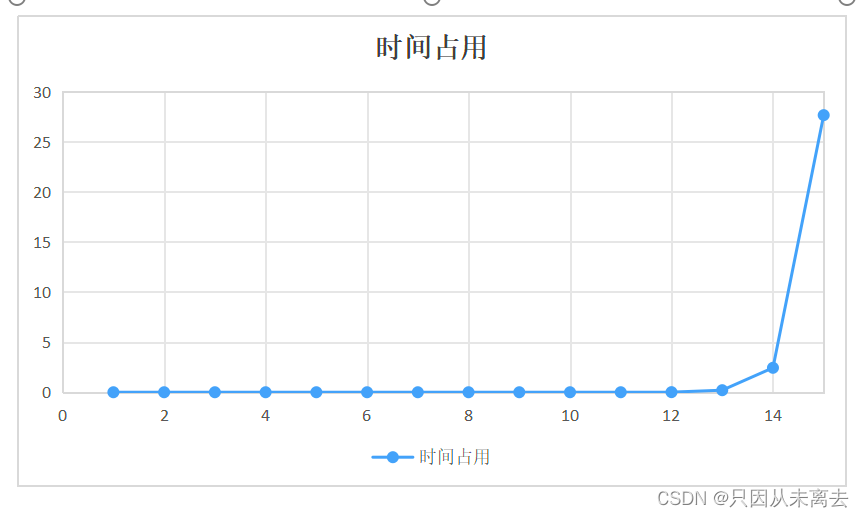
时间占用计算代码：

LARGE_INTEGER t1, t2, tc;
	QueryPerformanceFrequency(&tc);
	QueryPerformanceCounter(&t1);
	back(g, n, v, result, visited, count);
	QueryPerformanceCounter(&t2);

分析过程：

假设我们有n个节点，最好的情况就是没有边的结果，只要进入一次递归就行，时间复杂度为O（1）；

最复杂的情况是每个节点都与其他节点有相连的时候，我们只能开头确定一个节点，也就是初始节点，在递归树的第二层则有n-1个节点数需要递归，在第三层中每个节点又需要递归n-2个节点，也就是(n-1)(n-2)，在第四层中每个节点又需要递归n-3个节点，也就是(n-1)(n-2)(n-3),以此类推；

总共有n个节点，这棵递归树就有（n-1）！个叶子节点，所以时间复杂度就为O（（n-1）！）；

空间复杂度分析：

空间占用计算代码：

int space=(15*15*sizeof(int))//二维数组g[15][15]
	+ (3*sizeof(int))//n,count,i
	+ (v.capacity()*sizeof(int))//vector<int> v
	+ (sizeof(v))//vector v的三个指针
	+ (result.capacity()*(sizeof(v)+(v.capacity()*sizeof(int))))//vector<vector<int>> result
	+ (sizeof(result))//vector result的三个指针
	+ (visited.capacity()*sizeof(bool))//vector<bool> visited
	+ (sizeof(visited));//vector visited的三个指针

分析过程：

这边是我用来计算空间占用的代码，现在我来逐步分析空间复杂度：

二维数组g[15][15]：O(n^2);
n,count,i三个int型：O(1);
用来储存一条哈密顿回路vector<int> v：O(n);
vector v的三个指针：O(1);
存储结果的vector<vector<int>> result：O(n！);
vector result的三个指针：O(1);
储存走过节点的vector<bool> visited：O(n);
vector visited的三个指针：O(1);

可以发现空间复杂度最高的为vector<vector<int>> result有O(n！)。

n！的计算过程为，如果每个节点都与其他节点有相连的时候，也就是时间复杂度最复杂的情况，你会发现，递归的每条路径都是哈密顿回路，也就是（n-1）！条回路，result中就存在（n-1）！条vector<int>，每条vector<int>都有n个节点O(n)，所以空间复杂度就为（n-1）！*n=n！也就是O(n！)；

计算时间，空间复杂度数据的代码：

#include <iostream>
#include <iomanip>
#include <vector>
#include<windows.h>
#pragma comment( lib,"winmm.lib" )
using namespace std;

void back(int g[15][15], int n, vector<int> &v, vector<vector<int>> &result, vector<bool> &visited, int &count) {
	count++; // 增加执行次数
	if (v.size() == n) {
		if (g[v.back()][v.front()] == 1 && g[v.front()][v.back()] == 1) {
			result.push_back(v);
		}
		return;
	}
	for (int i = 0; i < n; i++) {
		if (g[v.back()][i] == 1 && !visited[i]) {
			visited[i] = true;
			v.push_back(i);
			back(g, n, v, result, visited, count);
			v.pop_back();
			visited[i] = false;
		}
	}
	return;
}

// 定义一个测试函数，用于生成随机连接矩阵，并调用你的代码，同时测量时间和次数
void test(int n) {
	// 生成随机连接矩阵
	int g[15][15];
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < i; j++) {
			if (i == j) {
				g[i][j] = 0; // 对角线元素为0，表示没有自环
			} else {
				g[i][j] = g[j][i] = rand() % 2; // 随机生成0或1，表示是否有边相连
			}
		}
	}
	vector<int> v;
	vector<vector<int>> result;
	vector<bool> visited(n, false);
	int begin = 0;
	v.push_back(begin);
	visited[begin] = true;
	LARGE_INTEGER t1, t2, tc;
	int count = 0;
	//计算时间占用
	QueryPerformanceFrequency(&tc);
	QueryPerformanceCounter(&t1);
	back(g, n, v, result, visited, count);
	QueryPerformanceCounter(&t2);
	//计算空间占用
	int space=(15*15*sizeof(int))//二维数组g[15][15]
	+ (3*sizeof(int))//n,count,i
	+ (v.capacity()*sizeof(int))//vector<int> v
	+ (sizeof(v))//vector v的三个指针
	+ (result.capacity()*(sizeof(v)+(v.capacity()*sizeof(int))))//vector<vector<int>> result
	+ (sizeof(result))//vector result的三个指针
	+ (visited.capacity()*sizeof(bool))//vector<bool> visited
	+ (sizeof(visited));//vector visited的三个指针
	cout << "节点数为 " << n << " 时";
	printf("	时间占用:%f秒", (t2.QuadPart - t1.QuadPart)*1.0 / tc.QuadPart);
	cout<<"	空间占用:"<<space<<"字节";
	cout<<"	递归次数为:" << count <<"次"<<endl;
	
}

// 定义一个主函数，用于循环测试不同的节点数
int main() {
	// 设置随机数种子
	srand(time(NULL));
	// 循环测试从1到15的节点数
	for (int n = 1; n <= 15; n++) {
		test(n);
	}
	return 0;
}

代码解释：

使用随机的连接矩阵来测试节点数从1到15的时间空间占用。

vector内存占用大小的计算：

vector的空间占用可以分为两部分，一个是vector的三个指针与vector的开辟内存：

vector为了保证性能会预设一部分内存，并且在这个内存被使用完毕后会重新开一个更大的内存（这个内存分配取决编译器），使用vector.capacity()可以获取这个vector的真实容量，而不是里面元素的数量。

使用vector.capacity()*sizeof（type）可以获取这个vector所开辟的总内存

vector的三个指针分别为：

_Myfirst：指向vector的第一个元素的地址，也就是vector的起始位置。
_Mylast：指向vector的最后一个元素的下一个位置的地址，也就是vector的结束位置。
_Myend：指向vector当前分配的内存空间的最后一个位置的下一个地址，也就是vector的容量位置。

使用sizeof（vector)可以获取这三个指针所占用的内存大小

将vector所开辟的总内存加上vector的三个指针就可以得出vector所占用的总内存；

有问题欢迎大家指出

只因从未离去

关注

1
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
应用回溯法算法解决哈密顿问题，时间空间复杂度分析

哈密顿回路的定义： G=(V,E)是一个图，若G中一条路径通过且仅通过每一个顶点一次，称这条路径为哈密顿路径。若G中一个回路通过且仅通过每一个顶点一次，称这个环为哈密顿回路。若一个图存在哈密顿回路，就称为哈密顿图。这段代码的思路是使用回溯法来寻找一个给定的图中是否存在哈密顿回路，即经过每个节点一次且仅一次的回路。回溯法是一种试探性的搜索方法，从一个起点开始，沿着可行的边逐步扩展路径，如果遇到死路，就回退到上一个节点，换一条边继续搜索，直到找到所有的回路或者遍历完所有的可能。定义一个二维数组g[15
复制链接

扫一扫