（回溯法）求无向图的所有哈密顿回路

给定一个无向图，由指定的起点前往指定的终点，用回溯法来进行解题时，最好的方法就是用递归算法，可以清晰明了的设置好每一步，由于哈密顿回路是所有顶点都需要经过且只能经过一次，所以需要设置一个解向量数组x[ ]来记录已经经过的顶点；那在判断每个边，经过每个点时，需要将可能从起点到达终点的路径都要记录下来，我们选择使用vector容器来记录每一个经过的路径。

vector<int> path

跟蛮力法有些相似，核心思想就是把当前访问的顶点所连接的所有顶点都用递归法访问一边，直到找到的最后一个顶点恰好为终点时，将路径进行输出。

void Ham(int i,int num,int x[],vector<int> path){
	if(num==1&&s[i][End])		//只剩最后一个点且刚好为终点 
	{path.push_back(End);
	 display(path);
	 return;}
	 else if(num==1)	return;		//减枝 
	 else if(num>1){
	 	for(int j=1;j<MAX;j++)
	 	 if(j!=End&&s[i][j]&&!x[j])		//满足下一落脚点 
	 	  {
		   	x[j]=1;
		   	num--;
		   	path.push_back(j);
		   	Ham(j,num,x,path);
		   	num++;				//回溯	
		   	x[j]=0;				//回溯 
		   	path.pop_back();	//回溯 
		   }
	 }
}

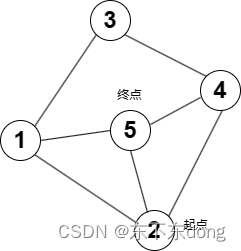
对应数组为s[MAX][MAX] ,为了方便,我将第一行与第一列置为0不使用.

int s[MAX][MAX]={{0,0,0,0,0,0},
				 {0,0,1,1,0,1},
				 {0,1,0,0,1,1},
				 {0,1,0,0,1,0},
				 {0,0,1,1,0,1},
				 {0,1,1,0,1,0}};

完整代码:

#include<iostream>
#define MAX 6
#include<vector>
using namespace std;
int s[MAX][MAX]={{0,0,0,0,0,0},
				 {0,0,1,1,0,1},
				 {0,1,0,0,1,1},
				 {0,1,0,0,1,0},
				 {0,0,1,1,0,1},
				 {0,1,1,0,1,0}};
int First;
int End;
void display(vector<int> path)
{
	for(auto p=path.begin();p!=path.end();p++)
	 {	if(p!=path.begin())
	 		cout <<"--->";
	 	cout<<*p;}
	cout<<endl;
}

void Ham(int i,int num,int x[],vector<int> path){
	if(num==1&&s[i][End])		//只剩最后一个点且刚好为终点 
	{path.push_back(End);
	 display(path);
	 return;}
	 else if(num==1)	return;		//减枝 
	 else if(num>1){
	 	for(int j=1;j<MAX;j++)
	 	 if(j!=End&&s[i][j]&&!x[j])		//满足下一落脚点 
	 	  {
		   	x[j]=1;
		   	num--;
		   	path.push_back(j);
		   	Ham(j,num,x,path);
		   	num++;				//回溯	
		   	x[j]=0;				//回溯 
		   	path.pop_back();	//回溯 
		   }
	 }
}

main()
{
int x[MAX]={0};
vector<int> path;
cout <<"输入起点和终点"<<endl;
 cin >>First;
 cin >>End;
 x[First]=1;
 path.push_back(First);
 Ham(First,MAX-2,x,path);
	return 0;
}

如有错误,欢迎指正