Algorithm U
Algorithm U (Uniform binary search). Given a table of records R1, R2,…, RN
whose keys are in increasing order K1 < K2< … < KN, this algorithm searches
for a given argument K. If N is even, the algorithm will sometimes refer to a
dummy key K0 that should be set to -Negative Infinite (or any value less than K). We assume
that N >= 1.
U1. [Initialize.] Set i <– ceil(N/2), m <– floor(N/2).
U2. [Compare.] If K < Ki, go to U3; if K > Ki, go to U4; and if K = Ki, the
algorithm terminates successfully.
U3. [Decrease i] (We have pinpointed the search to an interval that contains
either m or m-1 records; i points just to the right of this interval.) If m = 0,
the algorithm terminates unsuccessfully. Otherwise set i <– i-ceil(m/2); then
set m <– floor(m/2) and return to U2.
U4. [Increase i.] (We have pinpointed the search to an interval that contains
either m or m-1 records; i points just to the left of this interval.) If m = 0,
the algorithm terminates unsuccessfully. Otherwise set i <– i+ceil(m/2); then
set m <– floor(m/2) and return to U2. |
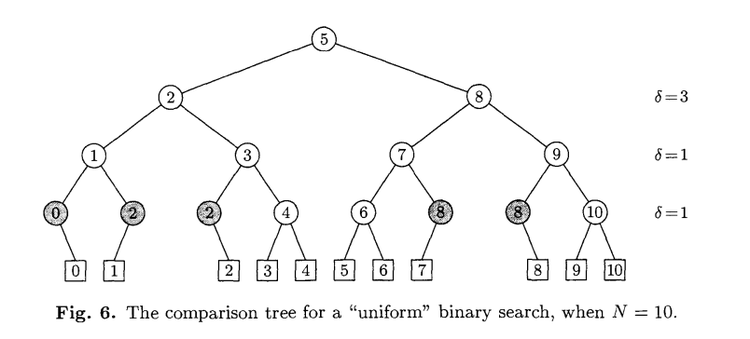
Comparison tree
Java program
In this program, R1,…,RN were simplified to K1,…,KN.
/**
* Created with IntelliJ IDEA.
* User: 1O1O
* Date: 12/10/13
* Time: 6:52 PM
* :)~
* Uniform Binary Search-1:Searching
*/
public class Main {
public static void main(String[] args) {
int N = 16;
int[] K = new int[17];
/*Prepare the ordered data table*/
K[1] = 61;
K[2] = 87;
K[3] = 154;
K[4] = 170;
K[5] = 275;
K[6] = 426;
K[7] = 503;
K[8] = 509;
K[9] = 512;
K[10] = 612;
K[11] = 653;
K[12] = 677;
K[13] = 703;
K[14] = 765;
K[15] = 897;
K[16] = 908;
/*Output sorted Ks*/
System.out.println("Sorted Ks:");
for(int i=1; i<=N; i++){
System.out.println(i+":"+K[i]);
}
System.out.println();
/*Kernel of the Algorithm!*/
int Key = 653; /*Key to be found*/
K[0] = -10000; /*Negative Infinite*/
int i = (int)Math.ceil((double)N/2);
int m = (int)Math.floor((double)N/2);
do{
if(Key < K[i]){
if(m == 0){
System.out.println("Outputs: "+Key+" not found.");
break;
}else {
i = i-(int)Math.ceil((double)m/2);
m = (int)Math.floor((double)m/2);
}
}else if(Key > K[i]){
if(m == 0){
System.out.println("Outputs: "+Key+" not found.");
break;
}else {
i = i+(int)Math.ceil((double)m/2);
m = (int)Math.floor((double)m/2);
}
}else {
System.out.println("Outputs: "+Key+" in K["+i+"].");
break;
}
}while (true);
}
}Outputs
Sorted Ks:
1:61
2:87
3:154
4:170
5:275
6:426
7:503
8:509
9:512
10:612
11:653
12:677
13:703
14:765
15:897
16:908
Outputs: 653 in K[11].Reference
<< The art of computer programming: Sorting and Searching >> VOLUME 3, DONALD E. KNUTH























 898
898

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








