本专栏用于记录关于深度学习的笔记,不光方便自己复习与查阅,同时也希望能给您解决一些关于深度学习的相关问题,并提供一些微不足道的人工神经网络模型设计思路。
专栏地址:「深度学习一遍过」必修篇
目录
1 激活函数
如果没有非线性激活函数:增加网络层数模型仍然是线性的。
 1.1 S 型激活函数
1.1 S 型激活函数
包 括 函数(常被代指
函 数 ) 与
函 数。

- 优点:输出0~1,映射平滑适合预测概率
- 缺点:不过零点,没有负值激活,影响梯度下降效率;饱和区梯度消失问题!
- 优点:映射到
之间,过零点,值域比
更大
- 缺点:饱和区梯度消失!
1.2 ReLU 激活函数
,修正线性单元
,正区间恒等变换,负区间
,
的平滑版本

- 优点:计算简单,导数恒定;拥有稀疏性,符合人脑的神经元活跃特性
- 缺点:非零中心化,没有负激活值,影响梯度下降效率;如果一次不恰当的参数更新后,所有数据都不能使某个神经元激活,则其对应的参数梯度为
,以后也无法激活,陷入‘死亡’(
)
改进
解决
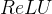 函数负区间的零激活问题。
휶
取固定值则为
函数负区间的零激活问题。
휶
取固定值则为
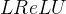 ,为可以学习的参数则为
,为可以学习的参数则为
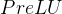 ,为随机值则为
,为随机值则为 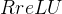 。
。

函数:有
的所有优点,并且不会有
问 题
:网络的浅层尤其是第一层卷积中,学习到的
会比较大,而到了深层就比较小。这可以理解为网络的浅层学习到了 类似于
的浅层特征,更大的
可以提取到更加稠密的特征,而随着网络深度的增加,特征变得更加的稀疏。
:当作一个正则项,用于增强网络的泛化能力。
![]() ,将
,将 函数
的那一端的函数取非线性函数。

- 优点:被证实有较高的噪声鲁棒性,能够使得神经元的平均激活均值趋近为0。
- 缺点:由于需要计算指数,计算量较大。
1.3 MaxOut激活函数


- 优点:整体学习输入到输出的非线性映射关系, 拟合能力非常强
- 缺点:计算量增加,增加了
个神经元
函数,

线性函数与 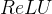 函数之间的非线性插值函数,无上界有下界、平滑非单调,从数据中学习参数
函数之间的非线性插值函数,无上界有下界、平滑非单调,从数据中学习参数 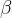 ,可以获得任务相关的激活机制。
,可以获得任务相关的激活机制。
import torchvision
from torch import nn
from torch.nn import Sigmoid
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
test_data = torchvision.datasets.CIFAR10('./dataset', train=False, download=True, transform=torchvision.transforms.ToTensor())
test_loader = DataLoader(dataset=test_data, batch_size=64)
class customize_model(nn.Module):
def __init__(self):
super(customize_model, self).__init__()
self.sigmoid1 = Sigmoid()
def forward(self, input):
output = self.sigmoid1(input)
return output
model = customize_model()
writer = SummaryWriter('./logs')
step = 0
for data in test_loader:
imgs, targets = data
writer.add_images('input', imgs, step)
output = model(imgs)
writer.add_images('output', output, step)
step = step + 1
writer.close()

2 线性层
import torchvision
from torch import nn
import torch
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
dataset = torchvision.datasets.CIFAR10('./dataset', train=False, transform=torchvision.transforms.ToTensor())
dataloader = DataLoader(dataset, batch_size=64)
class customize_model(nn.Module):
def __init__(self):
super(customize_model, self).__init__()
self.Linear1 = nn.Linear(6144*32, 10)
def forward(self, x):
x = self.Linear1(x)
return x
model = customize_model()
writer = SummaryWriter('./logs')
step = 0
for data in dataloader:
imgs, targets = data
print('原图shape:', imgs.shape)
writer.add_images('input', imgs, step)
# 法1°
output1 = torch.reshape(imgs, (1, 1, 1, -1))
# 法2°
output2 = torch.flatten(imgs)
output1 = model(output1)
output2 = model(output2)
print('(法1°)线性层shape:',output1.shape)
print('(法2°)线性层shape:', output2.shape)
print('*' * 50)
step = step + 1
writer.close()
3 卷积
import torchvision
from torch import nn
import torch
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
dataset = torchvision.datasets.CIFAR10('./dataset', train=False, transform=torchvision.transforms.ToTensor())
dataloader = DataLoader(dataset, batch_size=64)
class customize_model(nn.Module):
def __init__(self):
super(customize_model, self).__init__()
self.conv1 = nn.Conv2d(3,6,3,1,0)
def forward(self, x):
x = self.conv1(x)
return x
model = customize_model()
writer = SummaryWriter('./logs')
step = 0
for data in dataloader:
imgs, targets = data
output = model(imgs)
writer.add_images('input', imgs, step)
output = torch.reshape(output, (-1, 3, 30, 30))
writer.add_images('output', output, step)
step = step + 1
writer.close()
4 池化
,将一个区域的信息压缩成一个值,完成信息的抽象
依据步长和半径不同,可分为有重叠的池化和无重叠的池化。

最大池化:选取区域最大值(max pooling),能更好保留纹理特征。

平均池化:选取区域均值(mean pooling),能保留整体数据的特征。
随机池化:按照其概率值大小随机选择,元素被选中的概率与数值大小正相关
- 归一化
的输入,计算分布概率
。
- 从基于
的多项式分布中随机采样位置。
混合池化:max/average pooling中进行随机选择;增强泛化能力,类似于dropout机制
import torchvision
from torch import nn
from torch.nn import MaxPool2d
from torch.utils.data import DataLoader
from torch.utils.tensorboard import SummaryWriter
test_data = torchvision.datasets.CIFAR10('./dataset', train=False, download=True, transform=torchvision.transforms.ToTensor())
test_loader = DataLoader(dataset=test_data, batch_size=64)
class customize_model(nn.Module):
def __init__(self):
super(customize_model, self).__init__()
self.maxpool1 = MaxPool2d(kernel_size=3, ceil_mode=False)
def forward(self, input):
output = self.maxpool1(input)
return output
model = customize_model()
writer = SummaryWriter('dataloader')
step = 0
for data in test_loader:
imgs, targets = data
writer.add_images('input', imgs, step)
output = model(imgs)
writer.add_images('output', output, step)
step = step + 1
writer.close()
5 归一化
增强了信息的辨识度。
- 线性归一化
- 零均值归一化/Z-score标准化
- 直方图均衡化
作用:去除量纲干扰,保证数据的有效性,稳定数据分布

6 泛化
模型不仅在训练集表现良好,在未知的数据(测试集)也表现良好,即具有良好的泛化能力。

泛化不好的后果:模型性能不稳定,容易受到攻击
7 正则化
所谓正则化,它的目标就是要同时让经验风险和模型复杂度都较小,是对模型的一种规则约束。

即预测结果函数,
即损失函数。
跟模型复杂度相关的单调递增函数,用于约束模型的表达能力。
正则化的分类:
- 显式正则化(经验正则化,参数正则化)
网络结构,损失函数的修改,模型使用方法的调整 - 隐式正则化
没有直接对模型进行正则化约束,但间接获取更好的泛化能力
8 卷积神经网络卷积结果计算公式
- 长度:
- 宽度:
、
表示输入的宽度、长度
、
表示输出特征图的宽度、长度
表示卷积核长和宽的大小
表示滑动窗口步长
表示边界填充(加几圈
)
9 卷积神经网络反卷积结果计算公式
- 长度:
- 宽度:
、
表示输入的宽度、长度
、
表示输出特征图的宽度、长度
表示卷积核长和宽的大小
表示滑动窗口步长
表示边界填充(加几圈
)
























 3529
3529

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










