Best Time to Buy and Sell Stock III

leetcode中的股票问题（3）

来看看系列第三题咯

原题

Say you have an array for which the $i^{th}$ element is the price of a given stock on day $i$.
Design an algorithm to find the maximum profit. You may complete at most two transactions.
翻译：同样，一个表示每天价格的数组，同样要获得最大的收益，但是最多只允许你进行两手交易哟~

问题分析

相比于最多进行一手交易，这个问题就有点抽象啦，还是先上图：

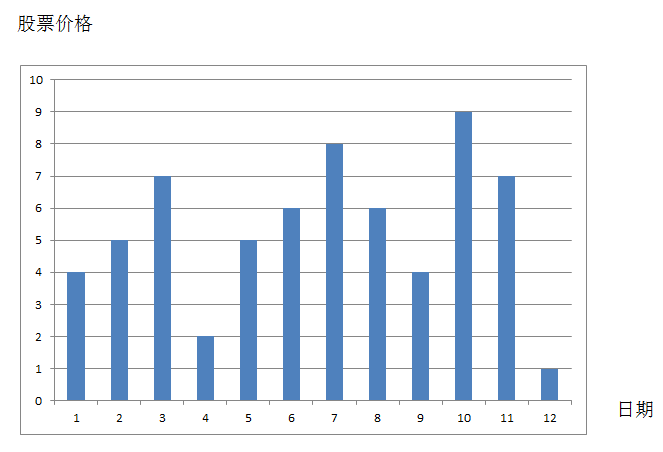
我们直观地猜一猜，大概也能猜出个答案吧~

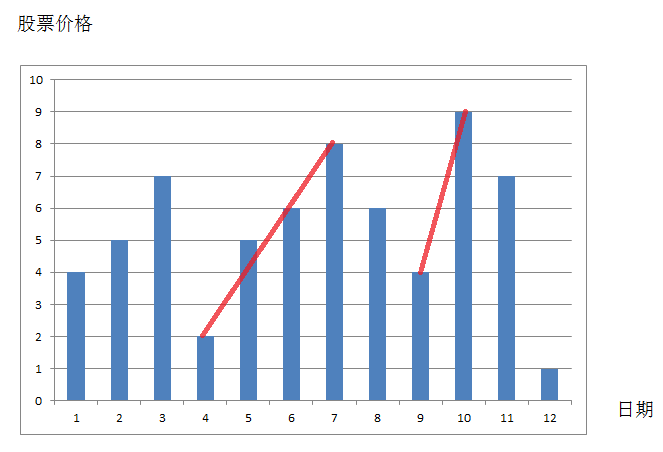
感觉得到，但是怎样去理解这两手交易呢？我的第一想法也是“分而治之”——对于某个坐标，左边做多允许一手，右边也是最多允许一手，这样一来，不就转化成两个“Best Time to Buy and Sell Stock I”中的子问题了吗？
但是问题来了，对于坐标i，其左边最多允许一手，按照“Best Time to Buy and Sell Stock I”中的方法，在$O(n)$的时间内可以做到，从左往右扫一遍即可，但是其右边的收益却要每次从i开始扫到末尾，复杂度是$O(n^2)$，是都不用试，肯定通不过大数据测试。
去Discuss上参考了别人的想法，发现从右往左扫可以解决这个问题，的确，我只要记住从右到目前的最大值，然后只要现价足够低，就更新最大收益的标记，基本和从左往右扫是相反的过程。
然后就简单啦，对于所有的i，把左右最大收益相加，取其中最大的就OK啦~

代码

public int maxProfit(int[] prices) {

    if(prices.length < 2)
    {
        return 0;
    }
    //left to right scan
    int[] left = new int[prices.length];
    //right to left scan
    int[] right = new int[prices.length];

    //for index i, find the max profit can be made
    //if at most one transaction can be completed before day i
    int minTag = prices[0];
    left[0] = 0;
    for(int i = 1; i < prices.length - 1; i++)
    {
        left[i] = Math.max(left[i - 1], prices[i] - minTag);
        minTag = Math.min(minTag,prices[i]);
    }

    //for index i, find the max profit can be made
    //if at most one transaction can be completed after day i
    int maxTag = prices[prices.length - 1];
    right[prices.length - 1] = 0;
    for(int i = prices.length - 2; i >= 0; i--)
    {
        right[i] = Math.max(right[i + 1], maxTag - prices[i]);
        maxTag = Math.max(maxTag,prices[i]);
    }

    int profit = 0;
    for(int i = 0; i < prices.length; i++)
    {
        //find the maximun profit
        if(left[i] + right[i] > profit)
        {
            profit = left[i] + right[i];
        }
    }
    return profit;
}