线性代数学习笔记3-1：矩阵与线性变换、常见矩阵（逆矩阵、伴随矩阵、正交矩阵等）

说明：接下来的内容，主要以二维空间举例说明，便于想象，理解后很容易推广到三维空间的情况

线性变换

之前说过，线性映射就是把向量映射成向量；而当线性映射发生在同一坐标系中，称为线性变换

“变换”就是“函数（映射）”，“变换”这个说法,暗示以运动的观点来可视化函数的输入-输出关系

变换的可视化

经过某个线性变换后，为了实现“可视化”（看出原来的点变到了什么位置），我们同时考虑原空间中的所有向量，并用运动的视角观察其变换

tips. 之前提过的技巧是，向量过多时，为避免过于混乱，此时简单用一个点代表一个向量，以便追踪变换前后的相对位置

最后，我们再把一个个点连成线，线和线交错为网格，观察网格的变化，就把握了整个空间（包括坐标轴）的线性变换

• 复杂的变换常给人挤压和变形空间的感觉（例如复数域的$f(z)＝e^z$等变换，图中白线为原来的x和y坐标轴）
  

• 好在线性代数中只研究特殊类型的变换——线性变换

线性变换

线性变换的判据（也就是“线性”的含义）：①可加性②比例性/齐次性

由这两个判决可以得到推论，作为简易的辅助判据：
①零向量经过线性变换，仍得到零向量（变换后原点位置不变）
②空间中任意直线在变换后仍为直线

最终，线性变换可以简单理解为“原点不变，且保持各网格线平行且等距分布”的变换，这是线性性（可加性和齐次性）在二维空间中的体现

后面还会介绍，引入矩阵后，矩阵右乘向量$\mathbf{A}\mathbf{x}$，一定是一个线性变换（满足上述两条线性性质）

矩阵：表示线性变换的工具

矩阵是学习线性代数的起点，从矩阵引申出后续的零空间、行列式、特征值等一系列概念

基本前提：坐标系问题

线性变换不一定依赖于具体坐标系；
但要具体、定量描述线性变换，需引入坐标系，矩阵基于坐标来描述线性变换（依赖不同坐标系，线性变换的矩阵不同）

我们当然可以直接描述一个线性变换（例如“投影到某直线”、“旋转某角度”等），而不依赖坐标系和矩阵
但是，如果需要确定变换的确切计算结果，则要引入特定的坐标系，从而才能使一个线性变换对应一个矩阵

• 注意，“坐标”是针对特定的基向量（坐标系）而言的，将向量写为基向量的线性组合$\mathbf{v}=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\dots +c_n{\mathbf{v}}_n$，则称$(c_1,c_2,...,c_n)$为坐标
• 只不过一般我们默认使用直角坐标系（标准正交基），因此我们意识不到基向量的存在

因此，下面的一切讨论，将线性变换对应到矩阵之前，都应该先明确：变换前的坐标系是什么、变换后的坐标系是什么，这样我们获得的向量坐标才是有效的

ps.以下不做特别说明，都是默认变换前后依赖于同一个坐标系（并且就是简单的直角坐标系），即：变换前后的向量坐标都是相对于同一个直角坐标系而言的
当然，也有可能变换前后依赖的坐标系不同，这种情况后面会专门讨论

• 总之，向量变换前/后 的坐标，都是针对特定坐标系而言的
• 后面会讲到，在不同坐标系下观察，同一个线性变换对应的矩阵不同

将线性变换表示为矩阵（变换前后在同一个坐标系下观察的情况）

只要知道基向量变换后的的新坐标，即可唯一表征一种线性变换
或者说一个线性变换，由它对基向量的作用完全确定，原因：

• 变换前，向量v是基向量的线性组合$\mathbf{v}=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\dots +c_n{\mathbf{v}}_n$；
• 变换后，根据线性变换的可加性和比例性，可得
  变换后的向量为$\mathbf{T}(\mathbf{v})=c_1\mathbf{T}({\mathbf{v}}_1)+c_2\mathbf{T}\left({\mathbf{v}}_2\right)+\dots +c_n\mathbf{T}\left({\mathbf{v}}_n\right)$
  其中$\mathbf{T}\left({\mathbf{v}}_i\right)$代表原来的基向量变换后的结果

（根据上述线性变换的比例性）可见，线性变换后的向量，只不过变为变换后的基向量的线性组合，其中的坐标值 /线性组合系数 /标量因子 $c_1...c_n$与变换前相同
（ $c_1...c_n$就是一个个数字，我们将其视为对基向量的缩放因子）
（从而矩阵向量乘法才有了合理性，向量变换前是基向量的怎么样的线性组合，变换后也是变换后的基向量的相同线性组合）

现在用线性代数语言描述问题：

在同一个坐标系下观察，如果
变换前，基向量为${\mathbf{v}}_1=\left[\begin{array}{cc}1& 0\end{array}\right],{\mathbf{v}}_2=\left[\begin{array}{cc}0& 1\end{array}\right]$，变换后为$\mathbf{T}({\mathbf{v}}_1)=\left[\begin{array}{cc}a& c\end{array}\right]$和$\mathbf{T}({\mathbf{v}}_2)=\left[\begin{array}{cc}b& d\end{array}\right]$

变换前，向量$\mathbf{v}=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2$，坐标$\mathbf{v}=\left[\begin{array}{cc}{c}_1& c_2\end{array}\right]$

则线性变换后，向量的新坐标为（坐标仍然基于原坐标系）$$\mathbf{T}(\mathbf{v})=c_1\mathbf{T}({\mathbf{v}}_1)+c_2\mathbf{T}\left({\mathbf{v}}_2\right)=c_1\left[\begin{array}{c}a\\ c\end{array}\right]+c_2\left[\begin{array}{c}b\\ d\end{array}\right]=\left[\begin{array}{cc}\mathbf{T}({\mathbf{v}}_1)& \mathbf{T}({\mathbf{v}}_2)\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\end{array}\right]=\mathbf{A}\mathbf{v}$$

可见，线性变换后，向量的新坐标，可以通过矩阵向量乘法得出：$\mathbf{T}(\mathbf{v})=\mathbf{A}\mathbf{v}$

• 矩阵$\mathbf{A}$左乘向量$\mathbf{v}$，几何意义就是对向量做线性变换
  其中$\mathbf{A}$的列向量对应变换后的基向量
  乘法结果为$\mathbf{v}$在线性变换后的新坐标（仍然基于原坐标系）
• 另一种理解是，任意向量做线性变换，就是基向量做线性变换，然后再（根据原来的坐标缩放并）叠加
  因此，矩阵乘以列向量，就是用原坐标去对「变换后的基向量」（列向量）做线性组合

至此，我们就实现了矩阵和线性变换的一一对应和互相转换

将线性变换表示为矩阵（推广：变换前后在不同坐标系下观察的情况）

基本原理前面说过：
变换前，向量$\mathbf{v}=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\dots +c_n{\mathbf{v}}_n$，坐标为$(c_1,c_2,...,c_n)$
变换后，向量变为$\mathbf{T}(\mathbf{v})=c_1\mathbf{T}({\mathbf{v}}_1)+c_2\mathbf{T}\left({\mathbf{v}}_2\right)+\dots +c_n\mathbf{T}\left({\mathbf{v}}_n\right)$，其中$\mathbf{T}\left({\mathbf{v}}_i\right)$代表原来的基向量变换后的结果

这里和上面的区别在于，变换前和变换后所依赖的坐标系不同
变换前，我们依赖的坐标系基向量为${\mathbf{v}}_1,{\mathbf{v}}_2,...,{\mathbf{v}}_n$
变换后，我们依赖的坐标系基向量为${\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_m$

• 由于变换后，在另一坐标系下观察，因此将变换后的基向量表示为（另一坐标系的）新的基向量的线性组合$$\begin{array}{l}\mathbf{T}\left({\mathbf{v}}_1\right)=a_{11}{\mathbf{w}}_1+a_{21}{\mathbf{w}}_2+\dots +a_{m1}{\mathbf{w}}_m\\ \mathbf{T}\left({\mathbf{v}}_2\right)=a_{12}{\mathbf{w}}_1+a_{22}{\mathbf{w}}_2+\dots +a_{m2}{\mathbf{w}}_m\\ \cdots \\ \mathbf{T}\left({\mathbf{v}}_n\right)=a_{1n}{\mathbf{w}}_1+a_{2n}{\mathbf{w}}_2+\dots +a_{mn}{\mathbf{w}}_m\end{array}$$这里的关键在于，描述变换结果时，所依赖的坐标系是另一个坐标系，因此需要在新坐标系下写出（第$i$个基向量变换后的）坐标$(a_{1i},a_{2i},...,a_{mi})$（也即：使用新坐标系的基进行线性组合所需要的系数），而不能像上面那样仍在原坐标系下写坐标

最终的结论是：$$\begin{gathered} [矩阵\mathbf{A}][输入向量的坐标(原坐标系下)]=[输出向量的坐标(新坐标系下)] \\ 其中，矩阵\mathbf{A}的第i个列向量为:第i个基向量变换后的坐标(a_{1i},a_{2i},...,a_{mi})(新坐标系下) \\ 即\mathbf{A}=\left[\begin{array}{ccc}\cdots & a_{1i}& \cdots \\ \cdots & a_{2i}& \cdots \\ \cdots & ⋮& \cdots \\ \cdots & a_{mi}& \cdots \end{array}\right] \end{gathered}$$

我们验证一下：第一个基向量变换后的坐标（在新坐标系下）
需要做的运算为$\mathbf{A}\left[\begin{array}{c}1\\ 0\\ ⋮\\ 0\end{array}\right]=\left[\begin{array}{c}{a}_{11}\\ a_{21}\\ ⋮\\ a_{m1}\end{array}\right](矩阵\mathbf{A}的第一个列向量)$，可见结果就是基向量变换后，在新坐标系下的坐标

将线性变换表示为矩阵（以特征向量建立坐标系来观察线性变换）

如果我们以线性变换的特征向量作为基向量，那么在这个新坐标系下，线性变换对应的矩阵就是一个对角阵（更加简洁）！

基本原理：
变换前，向量$\mathbf{v}=c_1{\mathbf{v}}_1+c_2{\mathbf{v}}_2+\dots +c_n{\mathbf{v}}_n$，坐标为$(c_1,c_2,...,c_n)$
变换后，向量变为$\mathbf{T}(\mathbf{v})=c_1\mathbf{T}({\mathbf{v}}_1)+c_2\mathbf{T}\left({\mathbf{v}}_2\right)+\dots +c_n\mathbf{T}\left({\mathbf{v}}_n\right)$，其中$\mathbf{T}\left({\mathbf{v}}_i\right)$代表原来的基向量变换后的结果

假如变换前后采用相同的坐标系，坐标系的基向量就是线性变换的特征向量：

• 变换后的基向量形式简单：
  （就是基向量本身的缩放，而不用像上面那样表示为基向量的线性组合）
  $$\begin{array}{l}\mathbf{T}\left({\mathbf{v}}_1\right)={\lambda }_1{\mathbf{v}}_1\\ \mathbf{T}\left({\mathbf{v}}_2\right)={\lambda }_2{\mathbf{v}}_2\\ \cdots \\ \mathbf{T}\left({\mathbf{v}}_n\right)={\lambda }_n{\mathbf{v}}_n\end{array}$$就是说，第$i$个基向量变换后的坐标为$(0,0,...{\lambda }_i,...,0)$（即：使用基进行线性组合所需要的系数）

最终的结论是（下述变换前/后坐标，始终针对同一个坐标系而言）：$$\begin{gathered} [矩阵\mathbf{A}][输入向量的坐标(原坐标系下)]=[输出向量的坐标(原坐标系下)] \\ 其中，矩阵\mathbf{A}的第i个列向量为:第i个基向量变换后的坐标(0,0,...{\lambda }_i,...,0) \\ 即\mathbf{A}=\left[\begin{array}{cccc}{\lambda }_1& 0& \cdots & 0\\ 0& {\lambda }_2& & 0\\ ⋮& & \ddots & ⋮\\ 0& \cdots & 0& {\lambda }_{\mathrm{n}}\end{array}\right] \end{gathered}$$

这说明，对于特定的线性变换，其特征向量给出了观察该变换的“完美坐标系”
也就是说，如果以线性变换的（矩阵的）特征向量作为观察坐标系的基向量，线性变换对应的矩阵就是简单的对角阵（对角元为特征值）
总之，观察一个线性变换，最好的观察坐标系由特征向量组成（沿着特征向量方向来观察线性变换，只存在基向量伸缩，不存在其他复杂变换）

原坐标系的基向量组成矩阵$\mathbf{V}$，线性变换的对应矩阵为$\mathbf{T}$
则上述变换过程写为：$\mathbf{T}\mathbf{V}=\mathbf{V}\mathbf{\Lambda }$，其中$\mathbf{V}$为$\mathbf{T}$的特征向量矩阵，$\mathbf{\Lambda }$为特征值组成的对角阵，由上得到$\mathbf{T}=\mathbf{V}\mathbf{\Lambda }{\mathbf{V}}^{-1}$，这就是相似对角化

线性变换对应的矩阵举例

1. 剪切/切变变换
   例如，在直角坐标系下观察，图中的矩阵表示，基向量${\mathbf{i}}^{\prime }$的新下标为(1, 0)，基向量${\mathbf{j}}^{\prime }$的新下标为(1, 1)，在原来的直角坐标系下画出，可以看出这是一种剪切/切变变换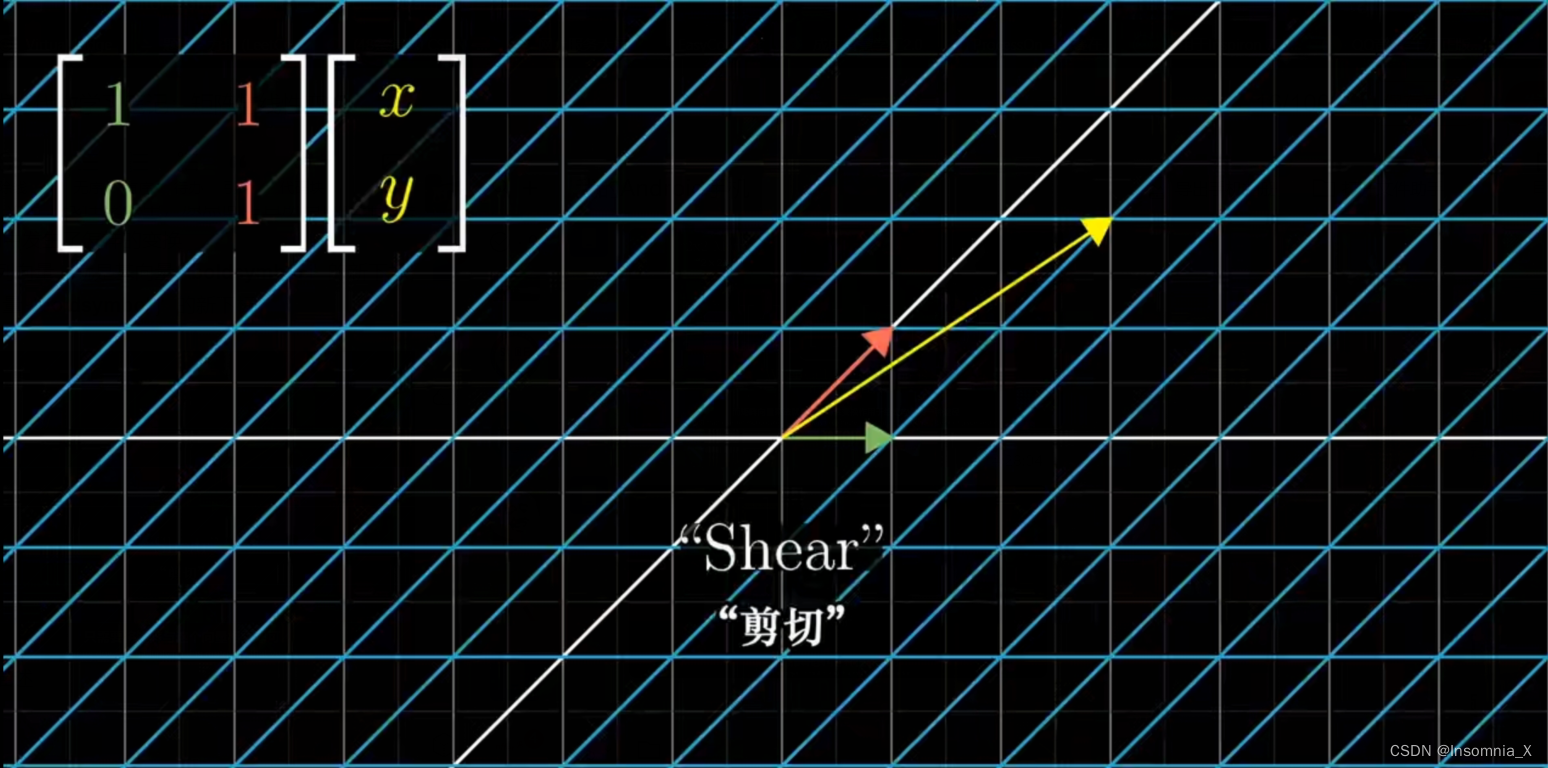
2. 降维/投影
   当矩阵的列向量线性相关时，此时矩阵对应的是线性变换降维的变换，或者说是一种投影
   原因：列向量线性相关，意味着变换后的基向量相关（新的基向量张成空间span的维度比原来低）

3 x 3 的矩阵列向量线性相关，原来有三个基向量，线性变换的结果维度从三维降低为二维
更一般的，这类线性变换实际上对应了以后会学习的投影矩阵

另外注意，2 x 3 的矩阵列向量线性相关，原来有三个基向量，但变换后的基向量都只有两个坐标分量，这是另一类“更直接”的降维线性变换：输入${\mathbf{R}}^3$空间向量，输出${\mathbf{R}}^2$空间向量

• 例如，在直角坐标系下观察（标准基$\mathbf{v}1=\left[\begin{array}{l}1\\ 0\end{array}\right],\mathbf{v}2=\left[\begin{array}{l}0\\ 1\end{array}\right]$），线性变换为：将任意向量投影到直线y=x上
  完成这个变换的投影矩阵$\mathbf{P}=\frac{{\mathbf{a}\mathbf{a}}^T}{{\mathbf{a}}^T\mathbf{a}}=\left[\begin{array}{ll}\frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& \frac{1}{2}\end{array}\right]$
  观察矩阵，其两个列向量相同（都在直线y=x上），这说明该变换会导致“降维”，与投影的意义一致

观察投影矩阵$\mathbf{P}=\left[\begin{array}{ll}\frac{1}{2}& \frac{1}{2}\\ \frac{1}{2}& \frac{1}{2}\end{array}\right]$，可以由几何意义或直接计算得出，其特征值${\lambda }_1=1,{\lambda }_2=0$，特征向量为$\left[\begin{array}{l}1\\ 1\end{array}\right],\left[\begin{array}{l}1\\ -1\end{array}\right]$

这里使用了直角坐标系，如前所述，也可以以特征向量建立坐标系并观察这个变换：

• 在倾斜45°坐标系下观察（以投影矩阵的特征向量为基$\mathbf{v}1=\left[\begin{array}{l}1\\ 1\end{array}\right],\mathbf{v}2=\left[\begin{array}{l}1\\ -1\end{array}\right]$），线性变换为：将任意向量投影到直线y=x上
  那么在该坐标系下，完成投影变换的矩阵$\mathbf{P}=\mathbf{\Lambda }=\left[\begin{array}{ll}1& 0\\ 0& 0\end{array}\right]$（实际上，对角线上就是特征值${\lambda }_1=1,{\lambda }_2=0$）
  观察矩阵列向量，对应于一个基向量在变换后不变，另一个基向量变换后消失，同样对应降维/投影

这里验证了，在不同坐标系下观察，同一个线性变换对应的矩阵也不同、观察一个线性变换，最好的坐标系由变换矩阵的特征向量组成

3. 求导$\mathbf{T}=\frac{d}{dx}$
   求导也是线性变换，满足线性的性质
   输入: $c_1+c_{2}x+c_3{x}^2+c_4{x}^3$，基：$1,x,x^2,x^3$
   输出: $c_2+2c_{3}x+3c_4{x}^2$，基：$1,x,x^2$
   可见，线性变换$\mathbf{T}：{\mathbf{R}}^4\to {\mathbf{R}}^3$，这是一个降维的变换
   因此，求导（线性变换）对应矩阵乘法$$\mathbf{A}\left[\begin{array}{l}{c}_1\\ c_2\\ c_3\\ c_4\end{array}\right]=\left[\begin{array}{c}{c}_2\\ 2c_3\\ 3c_4\end{array}\right]$$其中求导对应的矩阵为$\mathbf{A}=\left[\begin{array}{lllc}0& 1& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 3\end{array}\right]$（观察第一个列向量，代表原来的第一个基向量变换后消失，即常数求导为0）

对线性变换和矩阵的理解

• 线性变换是抽象本质，而矩阵是其具体表现
  矩阵的背后就是线性变换，相似矩阵描述的实际上是同一种线性变换在不同坐标系下的表现
• 如上所述，在不同坐标系下观察，同一个线性变换对应的矩阵也不同
• 矩阵对应线性变换，不应仅理解为矩阵与某一个、某几个向量相乘，而应将空间中任意向量视为输入，矩阵对整个空间进行了变换
• 线性变换两个含义是，变换空间里的向量,空间坐标系不变；或者变换坐标系而向量坐标不变。两者是相对的，结果等价

1. 矩阵乘以向量，得到的新向量的坐标相对于原坐标系而言的，在原坐标系下，对比变换前后的向量坐标，由此可以把线性变换理解为“坐标系不变，但是向量的坐标发生改变”；
2. 线性变换后，虽然基向量（坐标系）变了，但新向量在新坐标系中的坐标值不变（仍使用原来的标量），这就是说，线性变换也可理解为“向量坐标不改变，但线性变换后参考系/坐标轴/基向量变了”

• 逆矩阵就是线性变换的逆变换，线性变换不可逆对应矩阵不可逆
  矩阵与矩阵相乘，就是多个线性变换的叠加；因此今后可以将矩阵乘法视为连续的线性变换

矩阵与矩阵相乘的意义

矩阵与向量相乘，代表向量经历了某种线性变换，从一个向量变换到另一个向量

考虑相继发生的两次线性变换，第一次为旋转变换，第二次为剪切/切变变换：①首先用旋转变换的矩阵左乘原向量，得到新向量（中间结果）；②再用切边变换的矩阵左乘中间结果，就得到最终的新向量。

那么，两次变化的总体等效线性变换，由相应的两个矩阵的乘法给出

可见，矩阵相乘的意义是，两个线性变换的相继作用（连读变换坐标系）

注意：最先发生的变换，其对应的矩阵要放在右边，因为先发生的变换，应该优先与右侧的那个列向量结合

几类特殊的矩阵

有一些矩阵，其对应的线性变换较为特别

单位矩阵$\mathbf{I}$

在线性变换后，感觉“什么也没做”，对应的矩阵就是 单位矩阵$\mathbf{I}$

逆矩阵${\mathbf{A}}^{-1}$

应用 矩阵$\mathbf{A}$，发生某个线性变换后，空间会被拉伸/压缩变形；
我们进行“逆变换”，在变换后，将其恢复到原状，对应的矩阵就是逆矩阵${\mathbf{A}}^{-1}$
总体而言，两次变换的总效果是“什么也没做”，即$\mathbf{A}{\mathbf{A}}^{-1}=\mathbf{I}$

伴随矩阵

而伴随矩阵与逆矩阵密切相关，两者之间只差一个系数：${\mathbf{A}}^{-1}=\frac{{\mathbf{A}}^{\ast }}{|\mathbf{A}|}$（$det(\mathbf{A})=|\mathbf{A}|$）

注意，$det(\mathbf{A})=|\mathbf{A}|=0$（不满秩）时，逆矩阵不存在，意义是：由于原变换为压缩维度的变换，不存在对应的反向升维的矩阵（一对多映射就不是函数了）

伴随矩阵${\mathbf{A}}^{\ast }$也可以直接从原矩阵$\mathbf{A}$求出：伴随矩阵的每个元素就是原矩阵$\mathbf{A}$对应位置上的元素原矩阵$a_{ij}$的代数余子式（划去本行本列后的矩阵的行列式）

伴随矩阵的几何意义：伴随矩阵在几何空间的意义

奇异矩阵

方阵$\mathbf{A}$满足$det(\mathbf{A})=0⟺\mathbf{A}$为奇异矩阵$⟺\mathbf{A}$不是可逆矩阵
否则，$\mathbf{A}$为非奇异矩阵

正交矩阵

方阵$\mathbf{A}$满足${\mathbf{A}}^{\mathrm{T}}\mathbf{A}=\mathbf{A}{\mathbf{A}}^{\mathrm{T}}=\mathbf{E}$，也即${\mathbf{A}}^{-1}={\mathbf{A}}^{\mathrm{T}}$，称为正交矩阵

另外对于复矩阵有以下的概念推广：

复共轭转置/Hermite转置

${\mathbf{A}}^H=(\bar{\mathbf{A}}{)}^{\mathrm{T}}$

Hermite矩阵

理解为对称阵的复数推广

• ${\mathbf{A}}^H=\mathbf{A}$，矩阵$\mathbf{A}$为Hermite矩阵
• ${\mathbf{A}}^H=-\mathbf{A}$，矩阵$\mathbf{A}$为反Hermite矩阵

酉矩阵

理解为正交矩阵的复数推广
方阵$\mathbf{A}$满足${\mathbf{A}}^{\mathrm{H}}\mathbf{A}=\mathbf{A}{\mathbf{A}}^{\mathrm{H}}=\mathbf{E}$，也即${\mathbf{A}}^{-1}={\mathbf{A}}^{\mathrm{H}}$，称为酉矩阵

正规矩阵

其限制比 正交矩阵 弱一些

• 方阵$\mathbf{A}$满足$\mathbf{A}{\mathbf{A}}^{\mathrm{H}}={\mathbf{A}}^{\mathrm{H}}\mathbf{A}$，称为正规矩阵
• 方阵$\mathbf{A}$满足$\mathbf{A}{\mathbf{A}}^{\mathrm{T}}={\mathbf{A}}^{\mathrm{T}}\mathbf{A}$，称为实正规矩阵

补充说明：非方阵的情况

之前只讨论了方阵，但对于非方阵也是相同的道理：
比如一个3x2的矩阵

• 它有两列，代表变换前的基向量只有两个
• 每个列向量有三行，代表变换之后的基向量，其坐标是三维的（变换后的基向量用三个独立坐标来描述）

注意，这里不要认为是从二维到三维的“升维”：

1. 函数（映射）不可能做到升维（一对多），而是应该将原来的二维坐标系视为“三维空间的子空间”（在三维空间中描述的一个二维空间，或者说，可以将变换前的向量视为三维向量，但是其第三个维度始终为0）
2. 考察这个矩阵的列空间（见后续文章），由于变换后仍只有两个线性无关的基向量，故列空间是（三维空间中的）二维平面，也因此，这个矩阵是列满秩的（线性变换后空间没有被压缩，输入空间的维数=列空间的维数），这是同一维度的变换（仍然是一一映射），而非升维

同理，一个2x3的矩阵就代表三维空间到二维空间的变换（这里则可以理解为压缩降维，类似于投影的计算，这个投影操作将第三个维度压缩为0）

再进一步，一个1x2的矩阵（例如$[1,0]$矩阵）将二维平面压缩到一维直线上

• 与前面所说一致，1×2的矩阵中第一列（第二列）数值就是基向量i（基向量j）投影到该一维数轴上的投影值
• 这里可以和“点积”的投影意义结合理解
  因为1×2的矩阵左乘向量，等效于“两个列向量求点积”
  也就是说，“应用变换”和“与向量v做点积”是等价的，而这个v向量恰好就是矩阵的转置（几何意义就是做投影）

总结

• 线性变换是一种操纵空间和变换坐标轴的手段，它保持原点固定且网格平行等距。
• 可以简单的用一个矩阵来清楚的描述这个线性变换，该矩阵的列向量对应基向量变换后的坐标
• 将矩阵与向量的乘法，理解为矩阵各个列向量的线性组合，可帮助理解几何意义
• 矩阵给出了描述线性变换的语言（看到矩阵，脑海中就可以解读为对空间的缩放和偏斜等线性变换），而矩阵向量乘法可以计算线性变换作用于向量的效果
• 矩阵乘法对应于多次连续的线性变换，乘法的结果对应其总体等效的线性变换
• 今后应该从几何意义的层面来理解矩阵，看到矩阵乘法后先在脑海中思考相应的线性变换效果，然后再算出矩阵相乘的数值
  这样的思维会让一些证明也变得简单，例如矩阵的乘法结合律：$(\mathbf{A}\mathbf{B})\mathbf{C}=\mathbf{A}(\mathbf{B}\mathbf{C})$，从连续的线性变换来解读，一个是先做C变换，再做（B变换,A变换），另一个是先做（C变换,B变换），再做A变换，变换顺序都一致，两者当然就等效了