leetcode题解-48. Rotate Image

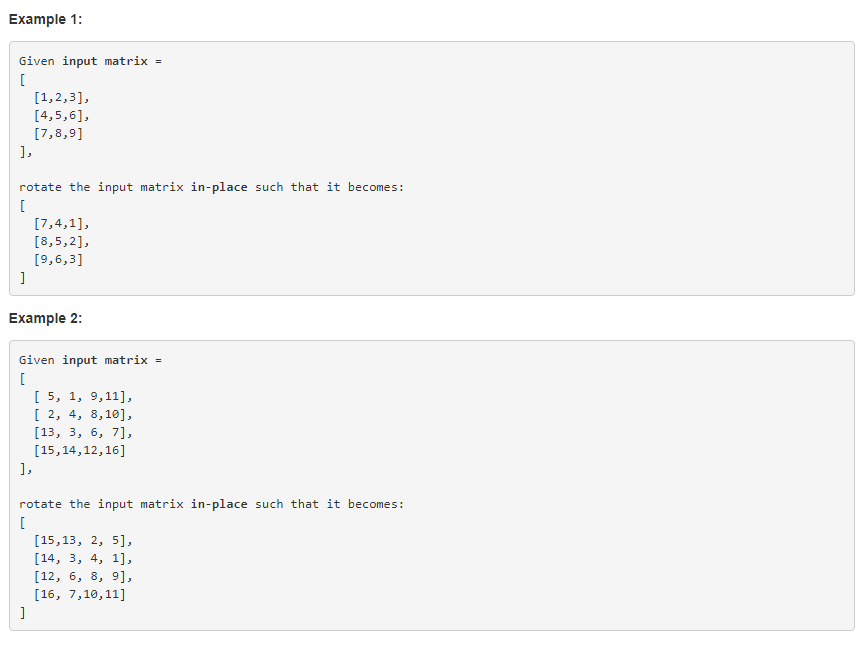
题目：给定一个n*n个2维矩阵来表示一个图。在原矩阵上顺旋转图形90°。
例子：

题解：在原矩阵的基础上进行操作（in-place），有两种方式：
1. 将原矩阵进行转置(transpose)，然后再左右对称进行翻转( flip it symmetrically)。
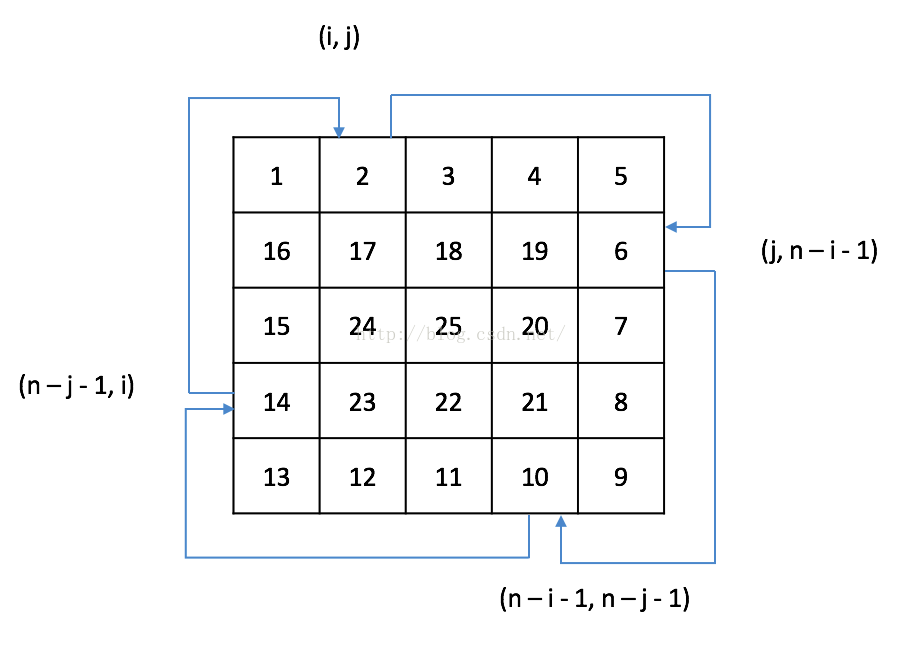
2. 找到数组元素在旋转前后的对应关系即可，以下图为例：

import java.util.Arrays;

public class Solution {
    public static void rotate(int[][] matrix) {
        // 1、first transpose, then flip
        // 2、模拟法
        int len = matrix.length;
        for(int i = 0; i < len / 2; i++){
            for(int j = 0; j < (len + 1) / 2; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[len - 1 - j][i];
                matrix[len - 1 - j][i] = matrix[len - 1 - i][len - 1 - j];
                matrix[len - 1 - i][len - 1 - j] = matrix[j][len - 1 - i];
                matrix[j][len - 1 - i] = temp;
            }
        }
    }
    public static void main(String[] args) {
        int[][] matrix = {
                          {1,2,3,4},
                          {5,6,7,8},
                          {9,10,11,12},
                          {13,14,15,16}
                        };
        rotate(matrix);
        for(int i = 0; i < 4; i++){
            for(int j = 0; j < 4; j++){
                System.out.print(matrix[i][j]+" ");
            }
            System.out.println();
        }

    }
}