说在前面
没什么好说的=w=(但是要保持格式)
题目

(原样例实在是太水了,我自己出了几组,在程序末尾)
解法
一个很经典的模型:”一张无向图从1走到N的必经点”
考试的时候写出来的程序在逻辑上有点问题,不过me的代码自带容错性,卡不掉的hhhhhh。不过还是决定把这个问题记录下来,以后方便复习。
可以发现,必经点一定是1到N路径上的某一个点(路径上每个点只能经过一次,不能1->u->v->u->N),me称之为路径点。那么只需要将所有这样的点先用一边dfs标记出来,然后再跑一遍tarjan求割点就好了。
相当于是要把图上的”枝丫点”给撇开不管,找剩下的图中的割点。
然而这样的”路径点”并不能用像下面这样的dfs去预处理:
bool acc[100005] ;
void dfs_acc( int u , int f ){
if( u == N ) acc[u] = true ;
for( int i = head[u] ; i ; i = p[i].pre ){
int v = p[i].to ;
if( v == f ) continue ;
dfs_acc( v , u ) ;
acc[u] |= acc[v] ;
}
}这个dfs的思路很简单,却存在漏洞。
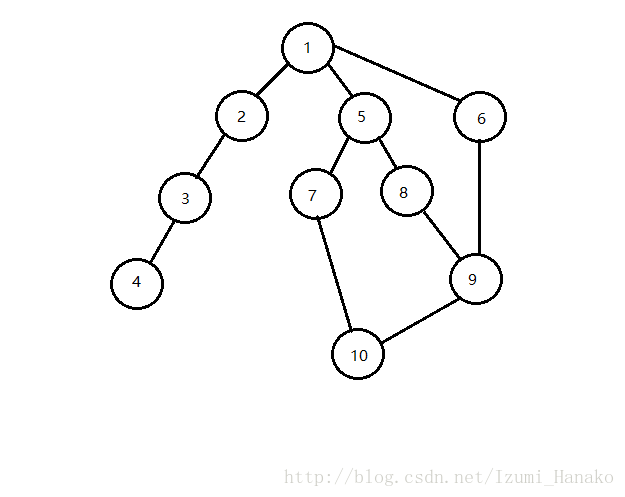
因为dfs是有先后顺序的。比如上面这个图,dfs顺序可能如下:
1->5->8->9->6->1->return,如果在9号节点先进入的是6号节点,那么6号节点就无法被标记为”路径点”。因此是无法先用一边dfs预处理的。
正确的做法是在tarjan的时候,无论点是不是路径点,都进去dfs一遍。如果在某一个u->v的时候有lowv ≥ dfn[u],并且v可以到达N点,u才是必经点。正确性是显然的,如果是v导致了u被判为割点,并且v还能到N点,那么说明N一定在v的子树内。这种情况下,1点必须经过u点才能走到N,可以感性理解一下。
因此严谨的逻辑是:先判断割点,再看导致该点被判为割点的点是否是”路径点”,如果是,那么该点就是割点。
而不严谨的逻辑是:先判断该点是路径点,再跑tarjan求割点。(其实这个逻辑是对的,但是实现过程会出错)
自带大常数的代码
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std ;
int T , N , M , tp , head[200005] , cnt ;
struct Path{
int pre , to ;
}p[4*200005] ;
void In( int t1 , int t2 ){
p[++tp].pre = head[t1] ;
p[ head[t1] = tp ].to = t2 ;
}
inline int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
bool iscut[200005] , acc[200005] ;
int dfn[200005] , dfs_c ;
int dfs( int u , int f ){
int lowu = dfn[u] = ++dfs_c ;
for( int i = head[u] ; i ; i = p[i].pre ){
int v = p[i].to ;
if( v == f ) continue ;
if( !dfn[v] ){
int lowv = dfs( v , u ) ;
lowu = min( lowu , lowv ) ;
if( lowv >= dfn[u] && acc[v] )
iscut[u] = true ;
} else lowu = min( dfn[v] , lowu ) ;
acc[u] |= acc[v] ;
}
return lowu ;
}
void solve(){
acc[N] = true ;
dfs( 1 , 0 ) ;
for( int i = 2 ; i < N ; i ++ )
if( iscut[i] ) cnt ++ ;
printf( "%d\n" , cnt ) ;
for( int i = 2 ; i < N ; i ++ )
if( iscut[i] ) printf( "%d " , i ) ;
printf( "\n" ) ;
}
void clear(){
dfs_c = tp = cnt = 0 ;
memset( head , 0 , sizeof( head ) ) ;
memset( dfn , 0 , sizeof( dfn ) ) ;
memset( acc , false , sizeof( acc ) ) ;
memset( iscut , false , sizeof( iscut ) ) ;
}
int main(){
freopen( "home.in" , "r" , stdin ) ;
freopen( "home.out", "w" , stdout) ;
T=read();
while( T -- ){
clear() ;
N=read(),M=read();
for( int i = 1 , u , v ; i <= M ; i ++ ){
u=read(),v=read();
In( u , v ) ; In( v , u ) ;
}
solve() ;
}
return 0 ;
}
/*
5
4 3
1 2
2 3
3 4
5 5
1 2
2 3
3 4
4 5
4 1
20 22
1 2
2 3
2 4
3 5
3 6
4 7
4 8
5 9
9 10
8 11
11 12
5 13
5 14
6 14
7 15
8 15
8 16
13 17
14 18
15 18
16 19
18 20
5 5
1 2
2 3
3 5
1 4
4 5
5 5
1 2
2 3
3 4
4 5
4 1
*/



























 504
504

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








