强化学习 学习记录（2）

Finite Markov Decision Processes（MDPs）

马尔可夫决策过程：
有限MDP中，state，reward，action 集合中的元素数都是有限的

MDP的动力学方程：
$$p(s^{{}^{\prime }},r|s,a)=Pr(S_t=s^{{}^{\prime }},R_t=r|S_{t-1}=s,A_{t-1}=a)$$
这个式子表示，当前时刻的状态和奖励仅和之前一刻的状态和行动有关于再之前的状态和行动都无关。

这个过程中的agent代表的是进行决策部分而environment 代表的是 agent的外部，这与现实意义上的概念又区别，比如以人为例子，当我们想举手时，大脑是我们的agent来控制这个行为，而我们的手臂是environment。
MDP的目标是最大化一个长期的累计奖励，或者说最大的长期累计奖励就是我们要实现的目标，那么如何量化长期获得的奖励的累计，我们以奖励序列组成的特殊函数来定义return（回报），最简单的形式就是累加：
$$G_t=R_{t+1}+R_{t+2}+....+R_T$$
G代表回报，T代表着终止time step
我们将从开始到终止的整个过程叫做一个episode，每个episode 都会以一个终止状态来结尾，然后后面会再接一个开始状态来开始一个新的episode。就好比我们打LOL开始选英雄就是开始状态，基地爆炸就是终止状态，一局就算一个episode。每个episode相互独立。针对于这种有始有终的任务叫做 episode task，但是有很多任务无法分辨何时算是开始何时算是结束，我们称这种为continuing task。针对这种任务如果继续使用上面的公式会使得G趋于无穷，因为T趋于无穷。所以会再每个reward上加一个折扣率$\delta \in (0,1)$。
$$G_t=R_{t+1}+\delta R_{t+2}+{\delta }^2{R}_{t+3}+...+{\delta }^k{R}_{t+k+1}$$
由于在后面两者都会用到，所以用一种表达方式来表示这两种task，核心思想就是把episode task 看成是 $R_T$后奖励为0的序列。所以可以统一表示为
$$G_t=\sum _{k=t+1}^T{\delta }^{k-t-1}{R}^k$$

value function就是在给定状态下，G的期望。用来估计一个策略的好坏。我一开始看的时候有点混乱没搞懂两者的区别在哪里，后来想了想明白了：return是已经发生了的，就是说state，action已经定下来的情况下计算reward 的和，而value function 是给定首个状态，由于后续动作（动作是依据状态相关的概率分布选择）状态都未知所以计算出来的是一个期望。用公式来表示就是
$$v_{\pi }(s)=E_{\pi }[G_t|S_t=s]$$
$v_{\pi }$表示的是策略$\pi (a|s)$下的value function,这种只给初始状态的叫做state-value function
$$q_{\pi }(s,a)=E_{\pi }[G_t|S_t=s,A_t=a]$$
这种给定初始状态和初始行动的叫做action-value function。

Bellman equation

value function 具有一个很重要的迭代性,下面进行推导
$$\begin{array}{rl}{v}_{\pi }& =E(G_t|S_t=s)\\ & =E(R_{t+1}+\delta G_{t+1}|S_t=s)\\ & =E(R_{t+1}|S_t=s)+\delta E(G_{t+1}|S_t=s)\end{array}$$
分别计算左右两部分

$$\begin{array}{r}E(R{}_t+1|S_t=s)=\sum _{r}r\cdot P(r|s)=\sum _{r}r\cdot (\sum _{a}P(r|s,a)\cdot P(a|s))=\sum _{r}r\cdot (\sum _a\sum _{s^{\prime }}P(r,s^{\prime }|s,a)\cdot \pi (a|s))\end{array}$$

$$\begin{array}{rl}E(G_{t+1}|S_t=s)& =\sum _g{G}_{t+1}\cdot P(G_{t+1}|S_t=s)=\sum _g{G}_{t+1}\cdot \sum _{s^{\prime }}P(G_{t+1}|s,s^{\prime })\cdot P(s^{\prime }|s)\\ & =\sum _{s^{\prime }}\sum _g{G}_{t+1}\cdot P(G_{t+1}|s^{\prime })\cdot P(s^{\prime }|s))\\ & =\sum _{s^{\prime }}E[G_{t+1}|S_{t+1}=s^{\prime }]\sum _a\sum _{r}P(r,s^{\prime }|s,a)\cdot \pi (a|s)\end{array}$$
把这两个在带回去得到：
$$\begin{array}{rl}{v}_{\pi }(s)& =\sum _a\pi (a|s)\sum _{s^{\prime },r}P(s^{\prime },r|s,a)[r+\delta E[G_{t+1}|S_{t+1}=s^{\prime }]]\\ & =\sum _a\pi (a|s)\sum _{s^{\prime },r}P(s^{\prime },r|s,a)[r+\delta v_{\pi }(s^{\prime })]\end{array}$$

action-value function也差不多
$$q_{\pi }(s,a)=\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\delta \sum _{a^{\prime }}\pi (a^{\prime }|s^{\prime })q_{\pi }(s^{\prime },a^{\prime })]$$

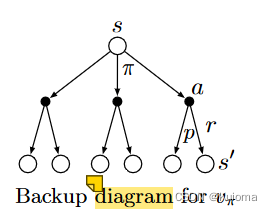
配合这幅图更好理解这个公式,图中的空心点代表状态，实心点代表行动。

最优策略

对于两个策略$\pi$,${\pi }^{\prime }$,如果对于任意状态存在$v_{\pi }(s)>=v_{{\pi }^{\prime }}$,那么就认为$\pi >={\pi }^{\prime }$,也就是$\pi$优于或等于${\pi }^{\prime }$。必然存在一个策略优于或等于所有其他策略，则称这个策略为最优策略,这个策略表示为${\pi }^{\ast }$。存在$v_{{\pi }^{\ast }}=max(v_{\pi })$,$q_{{\pi }^{\ast }}=max(q_{\pi })$。

$$\begin{array}{rl}{q}_{{\pi }^{\ast }}(s,a)& =E[R_{t+1}+\delta v_{{\pi }^{\ast }}(s^{\prime })|S_t=s,A_t=a]=E[R_{t+1}+\delta ma{x}_{a^{\prime }}{q}_{{\pi }^{\ast }}(S_{t+1},a^{\prime })|S_t=s,A_t=a]\\ & =\sum p(s^{\prime },r|s,a)[r+\delta ma{x}_{a^{\prime }}{q}_{{\pi }^{\ast }}(s^{\prime },a^{\prime })]\end{array}$$
$$v_{{\pi }^{\ast }}(s)=ma{x}_a{q}_{{\pi }^{\ast }}(a,s)=ma{x}_a\sum p(s^{\prime },r|s,a)[r+\delta v_{\ast }(s^{\prime })]$$

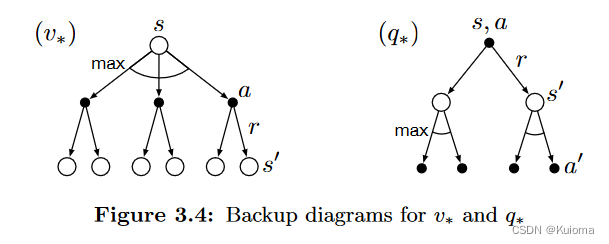
这两个公式根据上面的节点图就很好理解。
一开始对于这边还有个疑惑：就是如果全都是最优操作的话那么为什么还需要计算期望，直接全都加起来不就可以了。其实是这个environment的不确定性导致的，也就是说相同的行动在坏境中得到不同的状态，所得到的后续return也就不同，所以说还是需要计算期望
$${\pi }_{\ast }(a|s)=\{\begin{array}{l}1,a=argmax(q_{\ast }(s,a))\\ 0,otherwise\end{array}$$
也就是说最优化的策略是一个在固定状态下的固定选择，而不是一个概率分布