题目描述:
学校实行学分制。每门的必修课都有固定的学分,同时还必须获得相应的选修课程学分。学校开设了 N (N<300 )门的选修课程,每个学生可选课程的数量 M 是给定的。学生选修了这 M 门课并考核通过就能获得相应的学分。
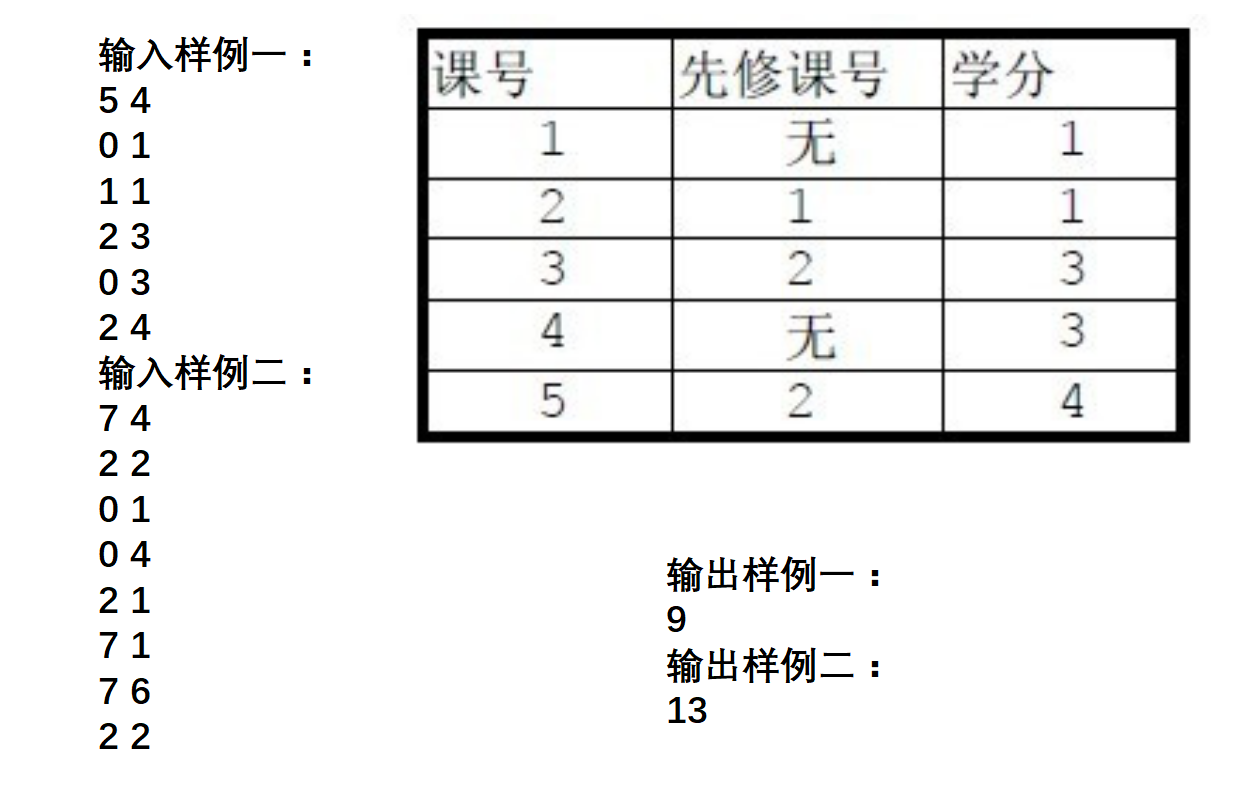
在选修课程中,有些课程可以直接选修,有些课程需要一定的基础知识,必须在选了其它的一些课程的基础上才能选修。例如《Frontpage》必须在选修了《Windows操作基础》之后才能选修。我们称《Windows操作基础》是《Frontpage》的先修课。每门课的直接先修课最多只有一门。两门课也可能存在相同的先修课。每门课都有一个课号,依次为 1,2,3,…。 例如:表中 1 是 2 的先修课,2 是 3、4 的先修课。如果要选 3,那么 1 和 2 都一定已被选修过。
你的任务是为自己确定一个选课方案,使得你能得到的学分最多,并且必须满足先修课优先的原则。假定课程之间不存在时间上的冲突。
输入:
输入文件的第一行包括两个整数 N 、M (中间用一个空格隔开)其中 1≤N≤300 ,1≤M≤N 。
以下 N 行每行代表一门课。课号依次为 1,2,…,N 。每行有两个数(用一个空格隔开),第一个数为这门课先修课的课号(若不存在先修课则该项为 0),第二个数为这门课的学分。学分是不超过 10 的正整数。
输出:
输出文件每行只有一个数。第一行是实际所选课程的学分总数。
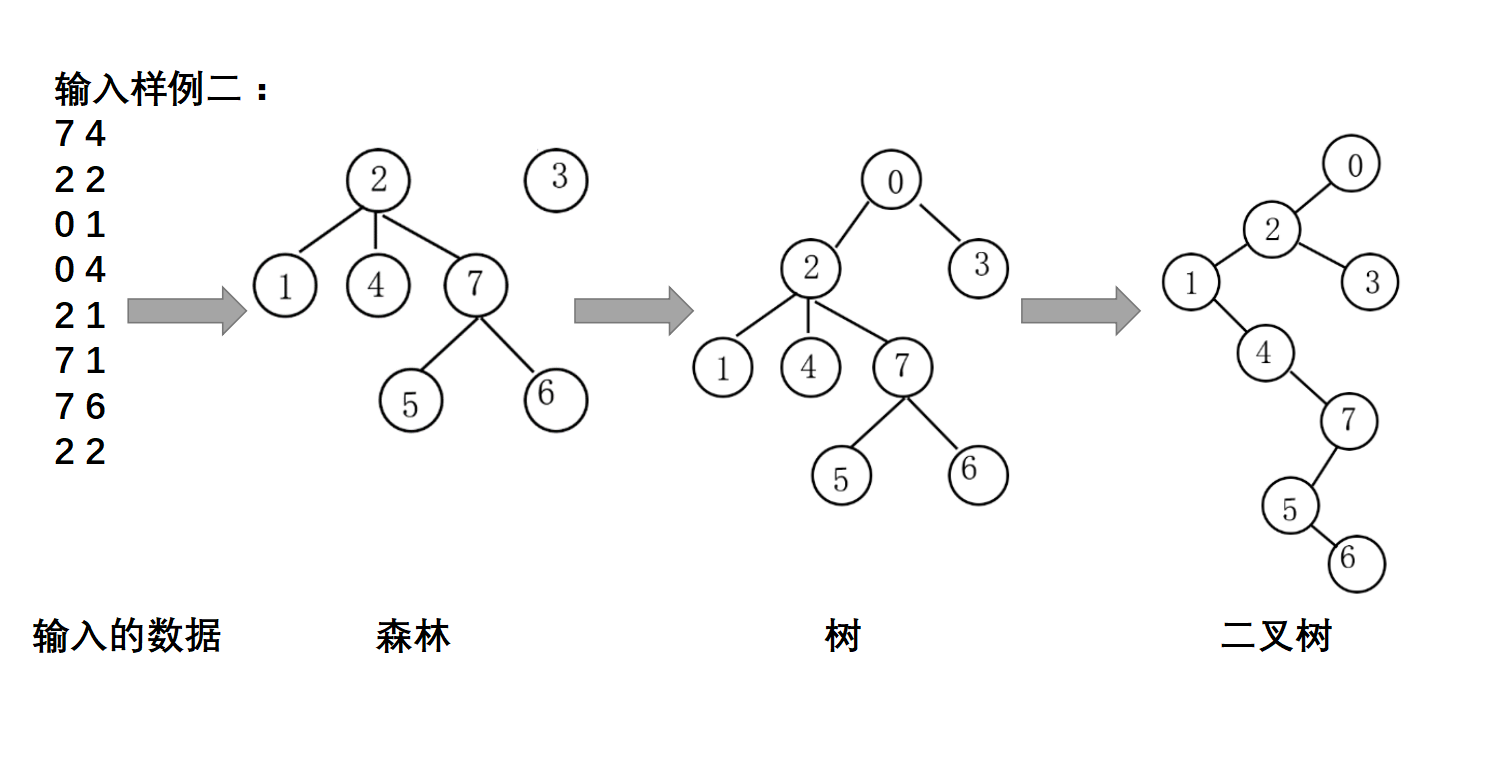
为了计算方便,首先肯定需要将森林装换为二叉树,方法数据结构书上有讲过。
动态规划方程:在树root中选取num项课程:
f[root][num]=max(
//不修root:在树b[root]中选取num项课程
f[b[root]][num],
//修root:在树c[root] 和树b[root] 中 共选取num-1项课程
score[root]+f[c[root]][k]+f[b[root]][num-k-1]
)
代码:
#include<iostream>
#define max(a,b) (a>b?a:b)
using namespace std;
//c[i]:i的child(左孩子);b[i]:i的brother(右孩子);score[i]:课程i的学分
//f[i][j]:在以i为根的树中选择j门课程的最高学分
int score[301],n,m,c[301],b[301],f[301][301];
void init();//输入数据并转化为孩子兄弟表示法的二叉树
int dfs(int root,int num);//使用记忆化搜索得出以root为根选num门可的最高学分
int main()
{
init();
cout<<dfs(c[0],m)<<endl;
return 0;
}
void init()
{
int t;
cin>>n>>m;
for(int i=1;i<=n;i++) {
//当前循环中,i为课程号,t为i的先修课,score为i的学分
cin>>t>>score[i];
//t的后修课程c[t]与i具有相同的先修课程t
b[i]=c[t];
c[t]=i;
}
}
//root:当前层的根编号,num:当前子树中应选课程数
int dfs(int root,int num)
{
if(!root||!num) return 0;
if(f[root][num]) return f[root][num];
//记录以root为根的树中,修课程root且选择num门课的最高学分
for(int k=0;k<num;k++)
f[root][num]=max(f[root][num],dfs(c[root],k)+dfs(b[root],num-k-1)+score[root]);
//比较 修或不修课程root所能达到的最高学分
return f[root][num]=max(f[root][num],dfs(b[root],num));
}
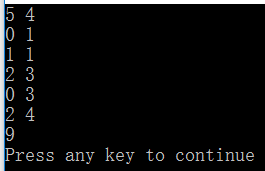
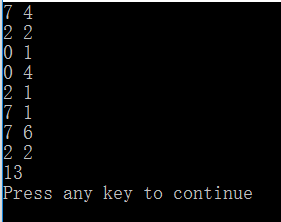
运行结果:
深搜+递归终止条件+记录运算结果 → 记忆化搜索
int dfs(int root,int num)
{
if(!root||!num) return 0;
if(f[root][num]) return f[root][num];
for(int k=0;k<num;k++)
f[root][num]=max(f[root][num],dfs(c[root],k)+dfs(b[root],num-k-1)+score[root]);
return f[root][num]=max(f[root][num],dfs(b[root],num));
}



























 426
426

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










