简析“自顶向下，逐步求精”的程序设计方法

概念

”自顶向下，逐步求精“是一种通过分解问题来逐步完成程序设计的方式。就好像我们经历过无数的考试一样，当你遇到一题数学题或者物理题时，你是怎样想问题和解决问题的呢？大概都是通过已知条件，逐步求解而得到最终的答案。而程序设计也与此类似，当你面对一个复杂的问题要用程序来解决时，不能直接解决或者太过于困难，你就可以将复杂的问题分解开来，由超级大分为大的、中的、小的、超小的，直到能用很直接的方法解决，最后逐个解决小问题，组合而解决大问题。

优点

• 程序的层次分明、结构清晰， 便于调试。

如果对问题没有分割，代码肯定是冗长，没有清晰的结构和层次，不利于对代码的调试。而通过“自顶向下，逐步求精”来设计，代码由许多小部分组成，出现问题时检查一个个小部分就可以找到bug所在，从而解决。

• 2.便于集体开发程序

通过“自顶向下，逐步求精”来设计，就可以将一个大程序分解成一个个小模块，交给团队不同人员来完成，便于集体开发程序，提高效率。

实例：用程序计算平面上四边形ABCD的面积，ABCD坐标已知。

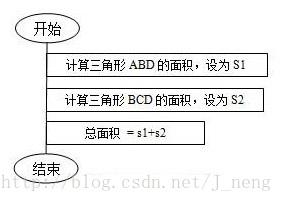
首先我们不知道四边形的样式，我们可以将它分成两个三角形再求面积和。

然后现在分解为求两个三角形的面积。
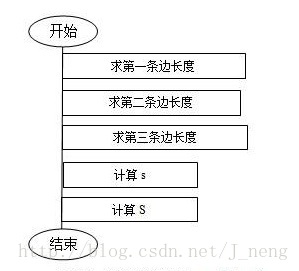
求三角形的面积，通过海伦公式

$$p=(a+b+c)/2)\\ S=sqrt[p(p-a)(p-b)(p-c)]\\ =sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]\\ =1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]$$
只需要三角形的边长就可以算出；

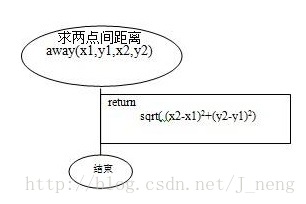
现在分解为求边长，此时可以直接实现。

最后此程序可由此组合而成。