考研 | 高等数学 Chapter1
文章目录
1. 迫敛定理 (夹逼定理)
- 数列型
设:
{ a n ⩽ b n ⩽ c n lim n → ∞ a n = lim n → ∞ c n = A \left\{\begin{array}{l} a_{n} \leqslant b_{n} \leqslant c_{n} \\ \displaystyle \lim _{n \rightarrow \infty} a_{n}=\lim _{n \rightarrow \infty} c_{n}=A \end{array}\right. {an⩽bn⩽cnn→∞liman=n→∞limcn=A
则:
lim n → ∞ b n = A \displaystyle \lim_{n \rightarrow \infty} b_n=A n→∞limbn=A - 函数型
设:
{ f ( x ) ⩽ g ( x ) ⩽ h ( x ) lim f ( x ) = lim h ( x ) = A \left\{\begin{array}{l} f(x) \leqslant g(x) \leqslant h(x) \\ \displaystyle \lim f(x) = \lim h(x) = A \end{array}\right. {f(x)⩽g(x)⩽h(x)limf(x)=limh(x)=A
则:
lim g ( x ) = A \lim g(x) = A limg(x)=A
2. 闭区间上连续函数的性质
-
最值定理
若 f ( x ) ∈ C [ a , b ] f(x)\in C[a, b] f(x)∈C[a,b], 则 f ( x ) f(x) f(x)在 [ a , b ] [a, b] [a,b]上一定存在最小值和最大值. -
有界定理
若 f ( x ) ∈ C [ a , b ] f(x)\in C[a, b] f(x)∈C[a,b], 则 f ( x ) f(x) f(x)在 [ a , b ] [a, b] [a,b]上一定有界. -
零点定理
若 f ( x ) ∈ C [ a , b ] f(x)\in C[a, b] f(x)∈C[a,b], 且 f ( a ) f ( b ) < 0 f(a)f(b)<0 f(a)f(b)<0, 则存在 ξ ∈ ( a , b ) \xi \in (a, b) ξ∈(a,b) , 使得 f ( ξ ) = 0 f(\xi) = 0 f(ξ)=0 -
介值定理
若 f ( x ) ∈ C [ a , b ] f(x) \in C[a, b] f(x)∈C[a,b], 对任意的 η ∈ [ m , M ] \eta \in [m, M] η∈[m,M], 存在 ξ ∈ [ a , b ] \xi \in [a, b] ξ∈[a,b], 使得 f ( ξ ) = η f(\xi) = \eta f(ξ)=η
4. 单调有界的数列必有极限
- 例一:

- 例二:

- 例三:

5. 几个重要的极限
- 当
x
→
0
x \rightarrow 0
x→0 时:
- x ∼ sin x ∼ tan x ∼ arcsin x ∼ arctan x ∼ e x − 1 ∼ ln ( 1 + x ) x \sim \sin x \sim \tan x \sim \arcsin x \sim \arctan x \sim e^x-1 \sim \ln(1+x) x∼sinx∼tanx∼arcsinx∼arctanx∼ex−1∼ln(1+x)
- 1 − cos x ∼ 1 2 x 2 1-\cos x \sim \frac12x^2 1−cosx∼21x2
- ( 1 + x ) a − a ∼ a x (1+x)^a-a \sim ax (1+x)a−a∼ax
- x − ln ( 1 + x ) ∼ 1 2 x 2 x-\ln(1+x) \sim \frac12x^2 x−ln(1+x)∼21x2
- 当
Δ
→
0
\Delta \rightarrow 0
Δ→0 时:
- sin Δ Δ = 1 \frac{\sin \Delta}{\Delta} = 1 ΔsinΔ=1
-
(
1
+
Δ
)
1
Δ
=
e
(1+\Delta)^\frac1{\Delta} = e
(1+Δ)Δ1=e
6. 0 / 0型
- u ( x ) v ( x ) ⇒ e v ( x ) ln u ( x ) u(x) ^ {v(x)} \Rightarrow e^{v(x)\ln {u(x)}} u(x)v(x)⇒ev(x)lnu(x)
- l n ( ) ⇒ ln ( 1 + Δ ) ; Δ → 0 ln() \Rightarrow \ln{(1+\Delta)}; \Delta \rightarrow 0 ln()⇒ln(1+Δ);Δ→0
- ( ) − 1 ⇒ e Δ − 1 ∼ Δ ⇒ ( 1 + Δ ) α − 1 ∼ α Δ ()-1 \Rightarrow e^{\Delta}-1 \sim \Delta \Rightarrow (1+\Delta)^\alpha-1 \sim \alpha\Delta ()−1⇒eΔ−1∼Δ⇒(1+Δ)α−1∼αΔ
- 例题
1.
lim x → 0 ( 1 + 2 x ) sin x − 1 x 2 = lim x → 0 e sin x ⋅ ln ( 1 + 2 x ) − 1 x 2 = lim x → 0 sin x ⋅ ln ( 1 + 2 x ) x 2 = lim x → 0 x ⋅ 2 x x 2 = 2 \begin{aligned} \lim _{x \rightarrow 0} \frac{(1+2 x)^{\sin x}-1}{x^{2}} &=\lim _{x \rightarrow 0} \frac{e^{\sin x \cdot \ln (1+2 x)}-1}{x^{2}}=\lim _{x \rightarrow 0} \frac{\sin x \cdot \ln (1+2 x)}{x^{2}} \\ &=\lim _{x \rightarrow 0} \frac{x \cdot 2 x}{x^{2}}=2 \end{aligned} x→0limx2(1+2x)sinx−1=x→0limx2esinx⋅ln(1+2x)−1=x→0limx2sinx⋅ln(1+2x)=x→0limx2x⋅2x=2
2.
lim x → 0 1 + tan x − 1 + x x 3 = lim x → 0 1 1 + tan x + 1 + x ⋅ tan x − x x 3 = 1 2 lim x → 0 sec 2 x − 1 3 x 2 ( sec x = 1 cos x ) = 1 6 lim x → 0 tan 2 x x 2 = 1 6 . \begin{aligned} & \lim _{x \rightarrow 0} \frac{\sqrt{1+\tan x}-\sqrt{1+x}}{x^{3}}=\lim _{x \rightarrow 0} \frac{1}{\sqrt{1+\tan x}+\sqrt{1+x}} \cdot \frac{\tan x-x}{x^{3}}\\ &=\frac{1}{2} \lim _{x \rightarrow 0} \frac{\sec ^{2} x-1}{3 x^{2}}\left(\sec x=\frac{1}{\cos x}\right)\\ &=\frac{1}{6} \lim _{x \rightarrow 0} \frac{\tan ^{2} x}{x^{2}}=\frac{1}{6} . \end{aligned} x→0limx31+tanx−1+x=x→0lim1+tanx+1+x1⋅x3tanx−x=21x→0lim3x2sec2x−1(secx=cosx1)=61x→0limx2tan2x=61.
7. 1的∞型
- 凑 ( 1 + Δ ) 1 Δ , Δ → 0 (1 + \Delta)^\frac1\Delta, \Delta \rightarrow 0 (1+Δ)Δ1,Δ→0
- 恒等变形
- 例题
1.
lim x → 0 ( 1 − x sin x ) 1 x − ln ( 1 + x ) = lim x → 0 { [ 1 + ( − x sin x ) ] 1 − x sin x } − x sin x x − ln + x + 1 = e − lim x → 0 x 2 1 2 x 2 = e − 2 \begin{aligned} &\lim _{x \rightarrow 0}(1-x \sin x)^{\frac{1}{x-\ln (1+x)}}=\lim _{x \rightarrow 0}\left\{[1+(-x \sin x)]^{\frac{1}{-x \sin x}}\right\}^{\frac{-x \sin x}{x-\ln +x+1}} \\ &=e^{-\lim _{x \rightarrow 0} \frac{x^2} {\frac12x^2}} = e^{-2} \end{aligned} x→0lim(1−xsinx)x−ln(1+x)1=x→0lim{[1+(−xsinx)]−xsinx1}x−ln+x+1−xsinx=e−limx→021x2x2=e−2
2.
lim x → 0 ( arcsin x x ) 1 x 2 = lim x → 0 { [ 1 + ( arcsin x x − 1 ) ] } arcsin x x − 1 x 2 = e lim x → 0 arcsin x − x x 3 = e lim x → 0 ( 1 − x 2 ) 1 2 − 1 3 x 2 = e − 1 2 − x 2 3 x 2 = e 1 6 \begin{aligned} &\lim_{x\rightarrow0}(\frac{\arcsin x}{x})^{\frac1{x^2}}=\lim_{x\rightarrow0} \{ [1 + (\frac{\arcsin x}{x} - 1)] \}^{\frac{\frac{\arcsin x}{x}-1}{x^2}}\\ &=e^{\lim _{x \rightarrow 0} \frac{\arcsin x-x}{x^{3}}}=e^{\lim _{x \rightarrow 0} \frac{\left(1-x^{2}\right)^{\frac{1}{2}}-1}{3 x^{2}}}=e^{\frac{-\frac{1}{2}-x^{2}}{3 x^{2}}}=e^{\frac{1}{6}} \end{aligned} x→0lim(xarcsinx)x21=x→0lim{[1+(xarcsinx−1)]}x2xarcsinx−1=elimx→0x3arcsinx−x=elimx→03x2(1−x2)21−1=e3x2−21−x2=e61
8. ∞/ ∞ 型
-
罗氏法则:
- 结论一:
lim x → + ∞ ln a x x b = 0 ( a > 0 , b > 0 ) \lim_{x\rightarrow+\infty}{\frac{\ln^ax}{x^b}} = 0\qquad(a>0, b>0) x→+∞limxblnax=0(a>0,b>0) - 结论二:
lim x → + ∞ x a b x = 0 ( a > 0 , b > 1 ) \lim_{x\rightarrow+\infty}{\frac{x^a}{b^x}} = 0 \qquad (a>0, b>1) x→+∞limbxxa=0(a>0,b>1)
- 结论一:
lim x → ∞ a m x m + ⋯ b n x n + ⋯ { = 0 , m < n = ∞ , m > n = a m b n , m = n \lim _{x \rightarrow \infty} \frac{a_{m} x^{m}+\cdots}{b_{n} x^{n}+\cdots} \quad \left\{\begin{array}{lll}=0, & m<n \\ =\infty, & m>n \\ =\frac{a_{m}}{b_{n}}, & m=n\end{array}\right. x→∞limbnxn+⋯amxm+⋯⎩⎨⎧=0,=∞,=bnam,m<nm>nm=n
9. ∞ - ∞
-
无分母:

-
有分母:

10. ∞ 和 0 的0次方
- 转成
e
ln
e^{\ln}
eln

11. Part 2
1. 连续
- lim x → a f ( x ) = f ( a ) ⇒ f ( x ) 在 x = a 上 连 续 \lim_{x\rightarrow a}f(x)=f(a) \Rightarrow f(x) 在 x=a 上连续 limx→af(x)=f(a)⇒f(x)在x=a上连续
-
{
f
(
x
)
在
(
a
,
b
)
内
处
处
连
续
,
f
(
a
)
=
f
(
a
+
0
)
,
f
(
b
)
=
f
(
b
−
0
)
\left\{\begin{array}{lll}f(x)在(a, b)内处处连续, \\ f(a)=f(a+0), f(b)=f(b-0) \end{array}\right.
{f(x)在(a,b)内处处连续,f(a)=f(a+0),f(b)=f(b−0)
则 f ( x ) 在 [ a , b ] 上 连 续 则f(x)在[a, b]上连续 则f(x)在[a,b]上连续
2. 间断
- I f lim x → a f ( x ) ≠ f ( a ) If \quad \lim_{x \rightarrow a}f(x) \neq f(a) Iflimx→af(x)=f(a), 间断
-
{
f
(
a
−
0
)
=
f
(
a
+
0
)
≠
f
(
a
)
,
a
为
可
去
间
断
点
f
(
a
−
0
)
≠
f
(
a
+
0
)
,
a
为
跳
跃
间
断
点
\left \{ \begin{array}{lll} f(a-0)=f(a+0)\neq f(a), \quad a 为可去间断点 \\ f(a-0) \neq f(a+0), \qquad\quad a为跳跃间断点 \end{array} \right.
{f(a−0)=f(a+0)=f(a),a为可去间断点f(a−0)=f(a+0),a为跳跃间断点

12. 介值定理
{
1.
函
数
值
之
和
2.
ξ
∈
[
a
,
b
]
\left \{ \begin{array}{lll}1.函数值之和 \\ 2.\xi \in [a,b] \end{array}\right.
{1.函数值之和2.ξ∈[a,b]

13. Note:
- sin ( x + y ) = sin x cos y + cos x sin y \sin(x+y)=\sin x\cos y + \cos x \sin y sin(x+y)=sinxcosy+cosxsiny
- sin ( x − y ) = sin x cos y − cos x sin y \sin(x-y)=\sin x\cos y - \cos x \sin y sin(x−y)=sinxcosy−cosxsiny
- cos ( x + y ) = cos x cos y − sin x sin y \cos (x+y) = \cos x\cos y - \sin x\sin y cos(x+y)=cosxcosy−sinxsiny
-
cos
(
x
−
y
)
=
cos
x
cos
y
+
sin
x
sin
y
\cos (x-y) = \cos x\cos y + \sin x\sin y
cos(x−y)=cosxcosy+sinxsiny
14. 习题:
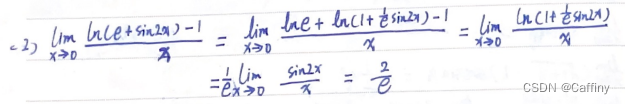







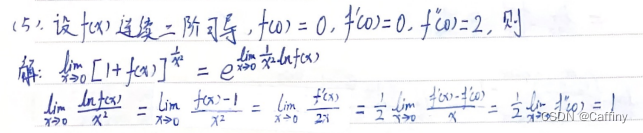































 251
251











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








