倍增,意思就是 “成倍增长”。
在进行 递推 时,如果 状态空间很大,通常的 线性递推 无法满足 时间 与 空间复杂度 的要求,那么我们可以通过 成倍增长 的方式,只递推 状态空间 中在 2 的整数次幂位置上的值 作为代表。
当需要 其他位置上 的值时,我们通过 “任意整数可以表示成若干个 2 的次幂项的和” 这一性质,使用 之前求出的代表值 拼成 所需的值。
所以使用 倍增算法 的一个基本要求:递推问题 的状态空间 关于 2 的次幂 具有 可划分性。
“倍增” 与 “二进制划分” 两个思想 互相结合,降低了求解很多问题的 时间 与 空间复杂度。
之前学习的 快速幂 其实就是 “倍增” 与 “二进制划分” 思想的一种体现。
在本篇中,我们研究 序列上的倍增问题,包括 求解RMQ(区间最值)问题 的 ST算法。
关于 求解最近公共祖先(LCA)等在树上的倍增应用,将在后续进行分析。


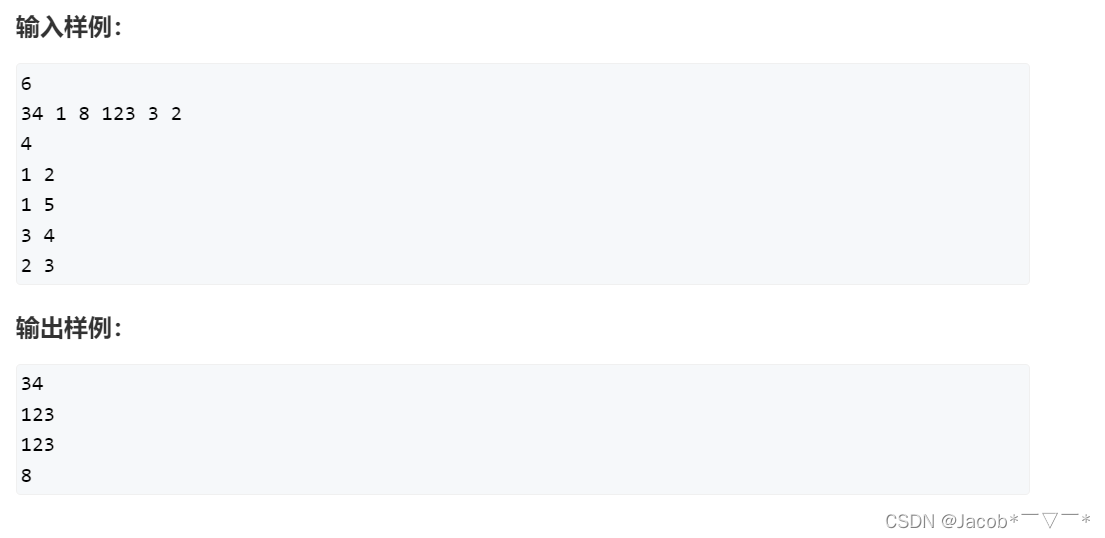
题意:
给定一长串数列,发出一系列询问:区间 [l,r] 中的 最大值,并输出结果。
数列中 元素个数范围<=2e5,询问个数<=1e4,显然不可以暴力求解。
思路:
对于这种 询问区间最大值 问题,当然做法可以有多种,比如之前探讨过的 线段树,
不过本题如果用线段树求解,其代码不免显得过于冗长了,
对于此类问题我们有一个专门的应对利器,那就是 RMQ算法(用于解决 区间最大值问题),其 代码短小,而且 常用。
首先要明确的一点是:RMQ算法 其本质其实是 动态规划,它还有其它的称谓:ST表、跳表。
其 总体思想 就是:先 倍增预处理,之后进行 快速查询。(缺点:是一个 静态算法,不支持修改)
接下来进行 dp分析:
f[i, j]状态表示:
从 i 开始,且长度为 2 ^ j 的区间中 最大值是多少。
举个例子就很清晰了,
求 区间 [i, j] 中的最大值,显然可以将 此区间 均分为 左右两区间,答案显然为 从两半区间的最大值之中 取 max 。
对于 左半边区间,根据定义可得:f[i, j - 1],右半边也易得:f[i + 2 ^ (j - 1), j - 1]。
最终得到 状态转移方程:f[i, j] = max(f[i, j - 1], f[i + 2 ^ (j - 1), j - 1])。(f[i][j] = max(f[i][j-1], f[i+(1<<(j-1))][j-1]);)
查询:
对于 查询 区间 [l, r] 中 的 最大值,设区间 [l, r] 的长度为 len,先找到 <=len 的 2 的最大整次幂 k,意味着,2 * 2 ^ k 一定 满足 > len,因此 严格覆盖整段 [l, r] 区间 最多 需要 两段 长度为 2 ^ k 的区间。
因此对于 查询区间 [l, r] 中的最大值,我们可以 分为两部分最大值取 max 进行分析:
- 从
l开始,长度为2 ^ k的区间最大值:f[l, k] - 从
r - 2 ^ k + 1开始,长度为2 ^ k的区间最大值:f[r - 2 ^ k + 1, k]
以O(1)的时间复杂度 进行 查询:max(f[l, k], f[r - 2 ^ k + 1, k])。(max(f[l][k], f[r - (1 << k) + 1][k]);)
对于上面说到的 k ,我们也可以进行 预处理,或者 直接使用 math库函数log(x)(此函数 以10为底),由于 k = log(2, len)(向下取整),根据 换底公式 可得 log(2, len) = log(10, len) / log(10, 2)(向下取整)
时间复杂度:
O(nlogn + q)
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+10, M = 18;
int n, q;
int a[N];
int st[N][M];
void init()
{
for(int j=0; j<M; ++j)
{
for(int i=1; i+(1<<j)-1<=n; ++i)
{
if(!j) st[i][j] = a[i];//当区间长度为 1 的时候直接赋值
else st[i][j] = max(st[i][j-1], st[i+(1<<(j-1))][j-1]);
}
}
}
int ask(int l, int r)
{
int len = r - l + 1;
int k = log(len) / log(2);
return max(st[l][k], st[r - (1 << k) + 1][k]);
}
int main()
{
cin>>n;
for(int i=1; i<=n; ++i) scanf("%d", &a[i]);
init();
cin>>q;
while(q--)
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", ask(l, r));
}
return 0;
}
关于 st表,我最近在牛客上做了一道好题,详情请戳 炸鸡块君与FIFA22。
 RMQ算法与区间最大值:倍增预处理与ST表详解
RMQ算法与区间最大值:倍增预处理与ST表详解











 本文探讨了如何使用倍增技巧解决区间最大值问题,通过ST表(RMQ算法)实现高效查询,适用于数列长度2e5及查询1e4的场景。介绍了状态转移方程和查询过程,以及代码实现和时间复杂度分析。
本文探讨了如何使用倍增技巧解决区间最大值问题,通过ST表(RMQ算法)实现高效查询,适用于数列长度2e5及查询1e4的场景。介绍了状态转移方程和查询过程,以及代码实现和时间复杂度分析。
















 2572
2572

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








