这篇博客的主要内容有:
1. 简述支持向量机(SVM)的一般记号
2. 介绍了函数间隔和几何间隔
3. 最大间隔分类器是什么
4. 为了得到最大间隔分类器解,而介绍了一些与拉格朗日有关的理论(拉格朗日乘数法,KKT条件,对偶性质)
5. 求解最大间隔分类器方法推导。其实推导出来的这个方法就是支持向量机。
支持向量机(SVM),通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
准备的记号
在支持向量机(Support Vector Machines(SVM))中我们使用的记号和之前的稍微有些不同。在这里:y∈{−1,1},分类器的表达式为:
令z=ωTx+b
上式也可以写成如下表达式:
其中: θ=[θ0,θ1...θn]T∈Rn
函数间隔和几何间隔(Functional and geometric margins)
给定一个训练集(x(i),y(i))可以给出函数间隔的表达式:
从这个式子可以看出,为了获得尽可能大的函数间隔:如果y=1时,表明分类结果正确。
我们将这个训练集上的函数间隔(样本的函数间隔)定义为:
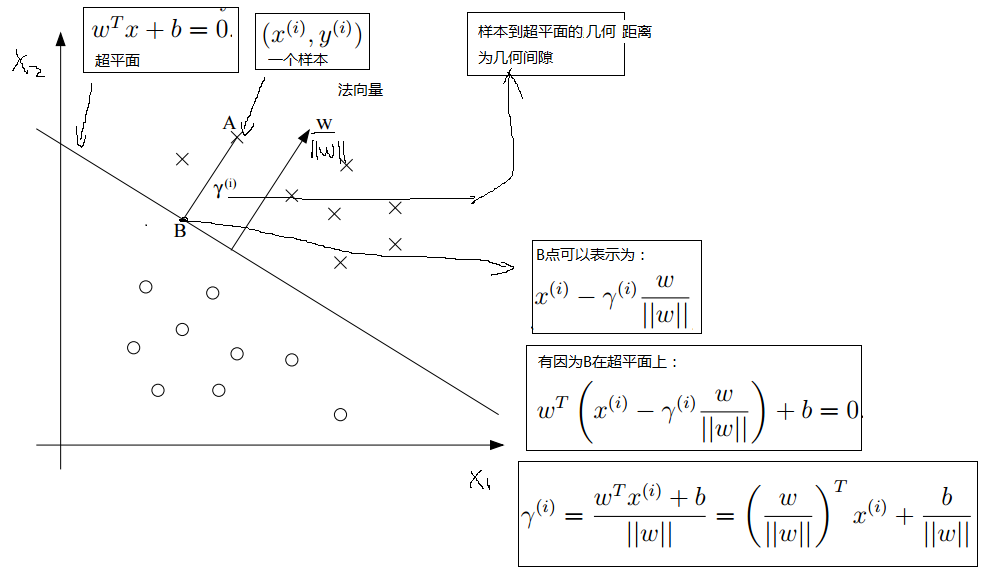
这个式子的意思很明显,我们要将最小的函数间隔作为训练集的的函数间隔。下来我们再来看看几何间隔:
经过上图的推导,我们最终得到了:
这个式子表明第i个训练样本到分隔平面的距离有参数ω,b这边总是好的,所以给出一个更加一般的定义形式:
对这个式子的理解是,我们认为自己的分类是正确的,并且希望各个训练样本距离分隔平面尽可能的元,只要他们还在平面的同一侧。对于同一侧的限制就是通过y(i),那么几何间隔就等于函数间隔。和函数间隔一样,我们定义整个训练集上的几何间隔(样本的几何间隔):
最大间隔分类器
现在我们已经有了间隔的定义,不管是函数间隔还是几何间隔。要完成一个分类问题,一种方式就是让这个间隔最大,然后我们就可以求出响应的参数。首先看看函数间隔,你给参数前乘一个大于零的数,函数间隔就会变大,这个不好。再来看看几何间隔,由于要将参数单位化,所以就不受参数的非因素影响,就是说当几何间隔最大的时候,真的就是训练样本距离超平面最大。这样用几何间隔就可以非常健壮的描述样本与超平面之间的距离。所以我们就构造下面这个优化问题:
这个优化问题中约束式子是函数间隔,但是在最后加上了一个||ω||=1是一个非常不好的约束条件,因为他的值在一个圆上或者在一个球体表面等等,这样我们就不容易利用梯度下降找到他的最有值。所以我们要将这个优化问题变形,而且尽可能的变形成一个凸优化的问题。如果了解最优化这门的话,你就会发现:这门课中介绍的所有算法都是求解凸优化问题的。而且现在对于凸优化问题我们非常成熟的解决方法以及软件,比如MATLAB中就有图形化的求解凸优化问题的工具箱。我们继续变形:
我们将||ω||指的是函数间隔。而目标函数这种相除的表示方式,意味的还是几何间隔。因为你把这个式子展开,就会看到,这就是几何间隔。当然我们还是要使得几何间隔最大。Andrew Ng老师说这还不是一个好的目标函数,而且没有办法用现成的软件和方法计算。那么我们继续变形。我在前面解释为什么不用函数间隔作为最优化的目标函数时,说过我们可以通过对函数间隔参数的变化使得它变大,那么我们同样可以利用参数的变化使得函数间隔变成我们想要的一种结果,比如1。可能你还是没有听懂我在说什么,看下面的式子,你就会发现他的魅力。
啊!这是怎么回事。
看到这个式子你可能就恍然大悟了,加上||ω||=1的最小化是等价的。目标函数通过这个变化变成了二次函数(凸的),前面的1/2是人为加的,为了计算方便,但是他不会影响问题的最优解。约束条件隐含的表明使用的是几何间隔。这样我们最优化的那一套就可以使用了,现成的软件也可以求解这个问题。
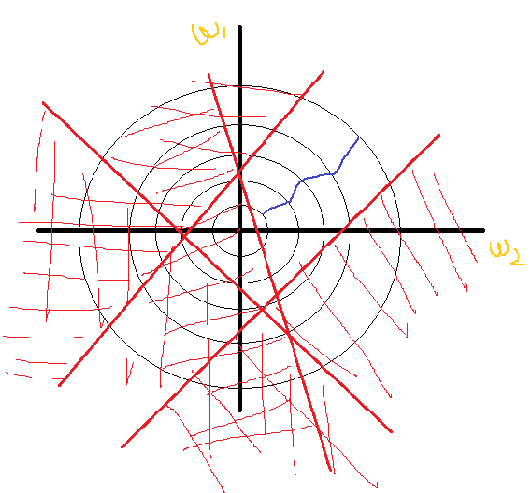
看这个图我们可以进一步理解我们构造的优化问题,横纵标标是ω1,ω2,黑色的圆圈表示目标函数的等高线,红色直线是约束条件,画斜线一个是不满足要求的;最后在第一象限就得到问题的可行域;蓝线使我们假设的梯度下降的轨迹。
总之,通过我们一步步变形,最终问题变成了一个凸二次优化问题。求加他,我们就可以得到一个超平面来分隔训练集。这个凸二次优化就是最大间隔分类器。下一步就是求解这个凸二次优化问题,得到的参数就是分隔训练集的超平面的参数。为了求解这个问题,我们还得知道一些与拉格朗日极值有关的理论。
一些与拉格朗日极值有关的理论
首先我们先回顾一下高数中讲的拉格朗日乘数法,它是为了求函数的极值。
这是我们的目标函数和约束条件。下一步是构造拉格朗日算子:
其中β称之为拉格朗日乘子。然后分别对参数进行求导,并令其为零:
然后求解方程组,将解得ω带入目标函数中,比较计算的结果,就可以得到目标函数的极值点。其实细细想来,拉格朗日乘数法就有点像是在求目标函数的驻点,然后在其中找极值点。
在实践中上面的目标函数有时候不能满足我们的的要求,所以我们要对它进行升级,得到下面目标函数:
这个问题和上面的问题非常相似,同样的数学家也给出了相似的解法,叫做增广拉格朗日函数。
下来我们在定义一个函数:
可以看出当gi(ω)>0:
如果约束条件成立,则这个函数和f(ω)相等。即:
我觉得这个函数可以称之为惩罚函数,意识就是如果在可行域之内这个函数就和原来的目标函数(f(ω))相等,如果在可行域之外这个函数的值就是无穷大,即就是对非可行域进行了惩罚。类似的你可以看最优化有关书籍中的外点罚函数法,内点罚函数法。
下面我们再构造一个最优化问题,其中下标p表示原问题(primal):
这式子的理解是:当不在可行域中时,由于有惩罚,目标函数求最小,就会迫使迭代向可行域方向走。当在可行域中时,θp(ω)=f(ω),原问题的无约束最优化。令:
p∗表示对偶的意思:
关于对偶理论可以参考 运筹学(第四版) 清华大学出版社 第64页
对偶问题的一些性质:
1. 目标函数值相同时,各自的解为最优解
2. 若原问题有最优解,那么对偶问题也有最优解,且目标函数值相同
3. 还有互补松弛性,无界性,对称性等等
如果d∗是对偶问题的最优值,即:
当原问题和对偶问题都取得最优解得时候,那么他们分别的目标函数也就到达了最优值。根据对偶问题的性质2,可以得到 d∗=p∗的最优值。
现在我们去求解还不行,得做一些假设。我发现数学家们无法将一个问题转换时,就直接假设。的确这也是一种解决问题的方式,但是假设一般都是增加限制条件。即就是损失了我们解决问题的关键。但是,目前我们无法转换,所以先只能这样了。或许会有人提出更好的方法。
现在我们就假设,假设的对象是:
我们假设f可以为零)之后就是仿射函数。仿射的意思是这个函数任何时候都是线性的。
有了这些假设我们就可以引出kkt(Karush−Kuhn−Tuckerconditions)。同样的我们可以根据对偶问题的性质得到:
那么这些最优解满足KKT条件:
最大间隔分类器的求解
已经走得太远了,让我们来回顾一下最大间隔分类器:
我们上面介绍了很多与拉格朗日有关的理论,就是为了利用他。首先我们就要将我们的问题标准化增广拉格朗日可以求解的的样子,下面是标准样子:
目标函数已经是标准好的,我们只需将约束条件进行标注化,如下:
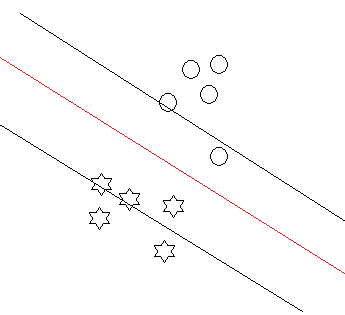
Andrew Ng老师说在实验中,KKT条件的乘子非负条件一般都是成立的,即αi>0就是几何间隔。看下图:
31.png
满足约束条件的训练样本(即在虚线上的样本)就是图中三个样本,这个三个样本我们称之为支持向量。一般的,支持向量都比较少,这个是可以理解的。也就是说大多数情况下都有αi=0,也就是说大部分训练样本到超平面的距离都是大于一的。Andrew Ng老师也说了,这个给的训练集都是可以用超平面分开的,也是可以找到支持向量的。更难的问题,我们后面再介绍解决的方法。
根据我们的最大间隔分类器,构造拉格朗日函数:
其中αi是拉格朗日乘子。
现在我们来看看他的对偶问题的一部分:
是一个求最值的问题我们可以利用拉格朗日乘数法的方式进行计算,分别对ω,b求导,并令为零:
可以得到:
再将上式带入问题的拉格朗日函数中,实质就是我们相对于ω:最小时,拉格朗日函数到底是什么?
下来我们在看完整的对偶问题:
而:
上面我们已经推导了拉格朗日函数求最小值的结果,并将结果用W(α),所以可以将这个对偶问题的优化形式写成如下形式:
对于这连个约束的解释是:第一个约束表明我们使用的是支持向量;第二个约束是我们在使得拉格朗日函数最小时得到的,如果它不等于零,那么θD(α,β)=−∞。我觉得这里还是带有惩罚。
这是一个有约束的二次优化问题,总之可以在最优化中找到求解方法,解的最优解为α∗使用拉格朗日乘数法得到的式子:
这样我们就可以求出ω就是选择哪个超平面的问题:
具体的计算公式是:
现在我们得到了参数ω,b,就可以完美的表示一个超平面了,这个超平面就可以训练集分成两类。这个求解算法就叫做支持向量机(support vector machines)。
总结
我觉得SVM最完美的地方就是它找到了一种通过求解对偶问题进而解决原问题的方法,我没查SVM和运筹学中的对偶理论的先后,但是可以看到将对偶理论应用于分类问题其实是一个艰难的探索过程。其中还用到了KKT条件,拉格朗日乘数法,所以说一个伟大发明其实不是一个人的功劳。








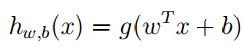
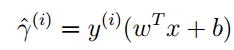
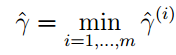
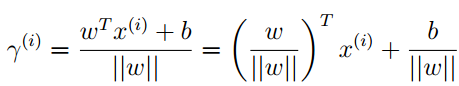
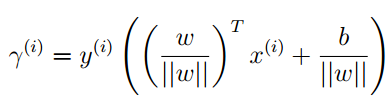
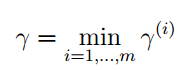
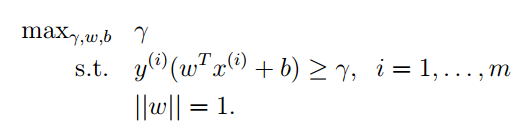
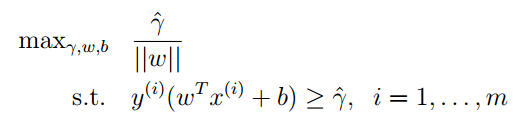
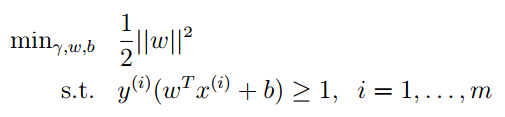
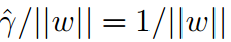
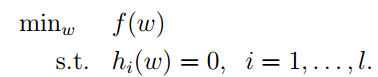
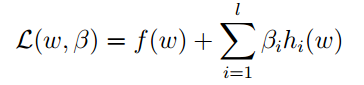
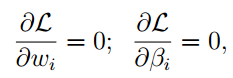
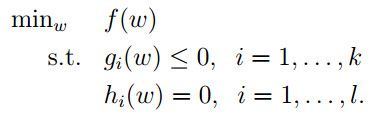
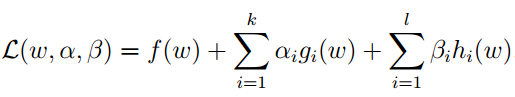
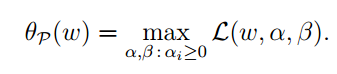
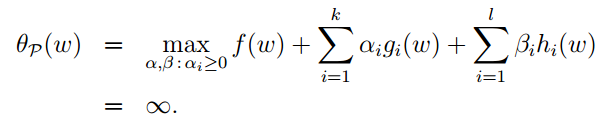
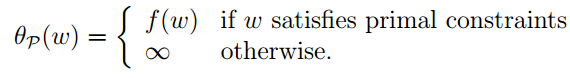
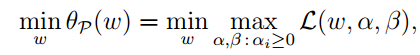
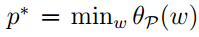
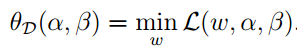
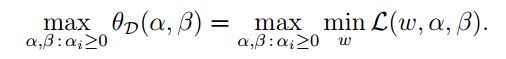
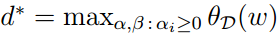
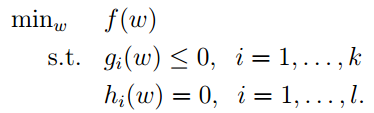
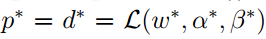

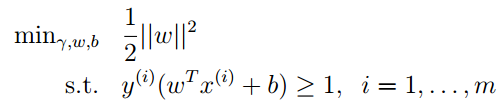
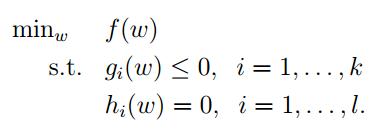
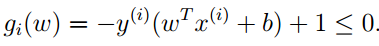
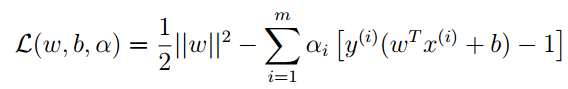
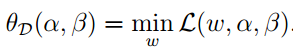
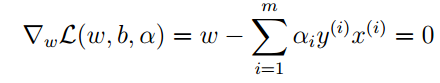
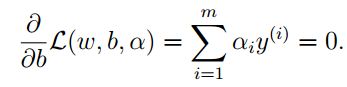
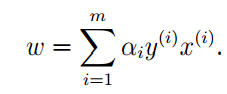
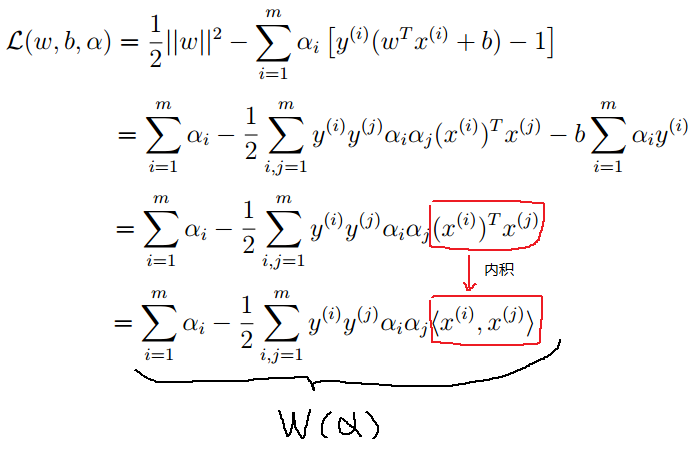
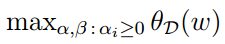
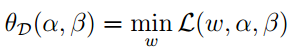
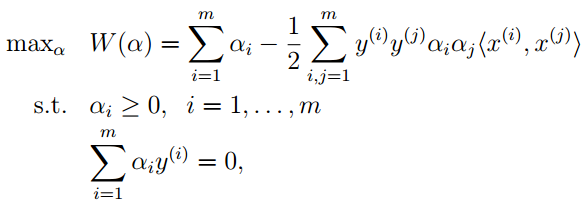
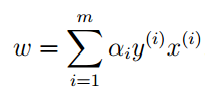
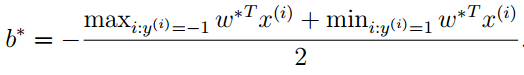
















 220
220

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








