超平面的定义

        研究了半天，终于对“超平面”有了个初步了解。

         n 维空间中的超平面由下面的方程确定:

                                                 

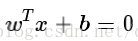
其中，w 和 x 都是 n 维列向量，x 为平面上的点，w 为平面上的法向量，决定了超平面的方向，b 是一个实数，代表超平面到原点的距离。且

                                

                             

                                                      

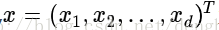
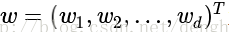
        那么，w 为什么是法向量呢？b 为什么表示平面到原点的距离呢？下面给出详细解释：

        我们对“平面”概念的理解，一般是定义在三维空间中的，即

                                                        

        这个平面由两个性质定义：1、方程是线性的，是由空间点的各分量的线性组合。2、方程数量是1。这个平面是建立在“三维”上的。如果我们撇开“维度”这个限制，那么就有了超平面的定义。实际上，超平面是纯粹的数学概念，不是物理概念，它是平面中的直线、空间中的平面的推广，只有当维度大于3，才称为“超”平面。它的本质是自由度比空间维度小1。自由度的概念可以简单的理解为至少要给定多少个分量的值才能确定一个点. 例如, 三维空间里的(超)平面只要给定了(x,y,z)中任意两个分量, 剩下的一个的值就确定了. 先确定值的两个分量是自由的, 因为它们想取什么值就能取什么值;剩下的那个是”不自由的”, 因为它的值已经由另外两确定了. 二维空间里的超平面为一条直线. 一维空间里超平面为数轴上的一个点。

        百度百科上对超平面的数学定义是这样的：超平面H是从n维空间到n-1维空间的一个映射子空间，它有一个n维向量和一个实数定义。因为是子空间，所以超平面一定过原点。

        通常，R2（二维空间）中的点集 i = （x,y）满足等式 (点集 i 实际为一条直线)：

                                              ax + 1/by + c = 0   (1)      (这里使用1/b 是为了后续计算好表示)

       其中，a，b，c均为标量，a，1/b至少有一个不为0.我们假设 b 不为0。，那么

                                               y = -abx  - cb 

        此时，使用换元法，令 t = x,（显然，t 为标量） 则点集 i (x,y) 可以表示成 

                                               i (x,y) =   ( t, -abt - cb） = t (1, -ab) + (0, -cb)

       这条直线是什么？实际上就是过 (0, -cb) 点，方向为 (1, -ab) 的直线 L。

        进一步，我们令向量 n  =  （a,1/b），则 （1）可以表示成n* i + c = 0  (2)

        神奇的一刻来临了。假设在直线 L 上取一点 p0(x0，y0），显然，n* p0 + c = 0，那么 c = -n* p0.

        更进一步，将 （2）改写，可得 n* i-n* p0 = 0 ，即可 n* （i - p0 ) = 0。

        因为 n 和（i - p0 ) 均是向量，（i - p0 ) 在直线 L 上， 所以，n 垂直直线L ,即n为直线L 的法向量。更进一步，我们可以得到，那些与p的差向量与 n 向量正交的点，就是点集 i (x,y).

       进一步解释什么是超平面：

        给定向量空间 Rn 中的一个点 P 和一个非零向量n ,满足

                                           n * （i - p）= 0

       则称点集 i 为通过点p 的超平面，向量 n为通过超平面的法向量。按照这个定义，虽然当维度大于3才可以成为“超”平面，但是你仍然可以认为，一条直线是 R2 空间内的超平面，一个平面是 R3 空间内的超平面 。Rn 空间的超平面是Rn 空间内的一个 n - 1 维的仿射子空间。

        样本空间中的任意一点 x，到超平面（w,b）的距离，可以表示为

                                                    

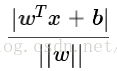
        判断超平面的正反

        一个超平面可以将它所在的空间分为两半, 它的法向量指向的那一半对应的一面是它的正面, 另一面则是它的反面。如果利用数学来判断的话，需要利用到法向量 w。

                                          

        若将距离公式中分子的绝对值去掉, 让它可以为正为负. 那么, 它的值正得越大, 代表点在平面的正向且与平面的距离越远. 反之, 它的值负得越大, 代表点在平面的反向且与平面的距离越远。