凸优化学习笔记<1>仿射集合和凸集

直线和线段

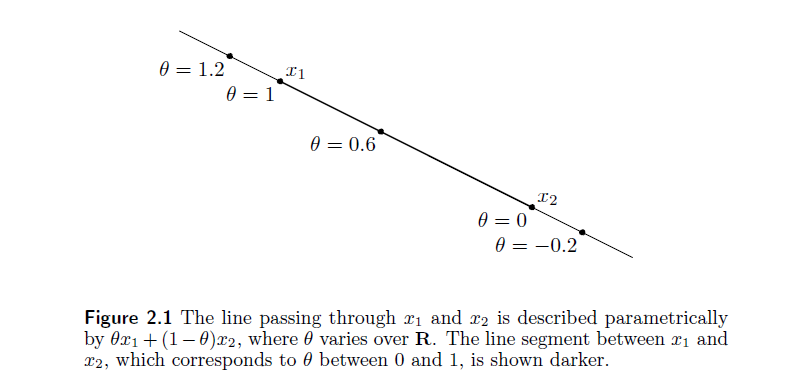
设$x_1$和$x_2$为${\mathbf{R}^n}$空间中两个点，且$x_1\neq x_2$，那么

$$y = \theta x_1+( 1-\theta) x_2, \theta \in \mathbf{R}$$
组成了一条穿过$x_1$和$x_2$的直线。如果$\theta=0$，则$y=x_2$，如果$\theta=1$，$y=x_1$。当$\theta\in[0,1]$时，$y$组成了$x_1$和$x_2$之间的线段。

彷射集合

如果有集合$C\subseteq\mathbf{R}^n$，且穿过集合$C$中任意两点的直线仍然在集合$C$中，则称该集合是仿射的。用公式来表达就是：$\forall x_1,x_2\in C$及$\theta\in \mathbf{R}$，都有$\theta x_1+( 1-\theta) x_2\in C$。也就是说，集合$C$包含$C$中任意两点系数和为1的线性组合。
推广到多个点。如果$\theta_1+\cdots +\theta_k=1$，则称$\theta_1x_1+\cdots +\theta_kx_k$为$x_1,\cdots,x_k$的彷射组合。一个仿射集合包含集合内任意点的仿射组合，即如果$C$仿射，$x_1,\cdots,x_k\in C$，且$\theta_1+\cdots +\theta_k=1$，则一定有$\theta_1x_1+\cdots +\theta_kx_k\in C$。
如果集合$C$仿射,且$x_0\in C$，则集合

$$V=C-x_0=\{x-x_0|x\in C\}$$
是一个子空间。
证明：
设$v_1,v_2\in V$,$\alpha,\beta\in\mathbf{R}$,根据$V$的定义有$v_1+x_0\in C,v_2+x_0\in C$。容易看出
$$\alpha v_1+\beta v_2+x_0=\alpha(v_1+x_0)+\beta(v_2+x_0)+(1-\alpha-\beta)x_0,$$
因为$C$仿射且$\alpha+\beta+(1-\alpha-\beta)=1$，可以得出$\alpha v_1+\beta v_2+x_0\in C$，即$\alpha v_1+\beta v_2\in V$，也就是说集合$V$对加法和数乘是封闭的，因此$V$是一个子空间。
我们称集合$C\in \mathbf{R}^n$中点的所有仿射组合构成的集合为$C$的仿射包。记为$\textbf{aff}C$。
$$\textbf{aff}C=\{ \theta_1x_1+\cdots +\theta_kx_k|\theta_1,\cdots,\theta_k\in C,\theta_1+\cdots+\theta_k=1 \}.$$
仿射包是包含$C$的最小的仿射集合，也就是说，如果$C\subseteq S$，且$S$仿射，则有$\textbf{aff}C\subseteq S$。该证明平凡。

几个例子：

1. 单点集的仿射包是它本身。
2. 包含两个点(两点不同）的集合的仿射包是穿过它们的直线。
3. 包含三个点(三点不共线)的集合的仿射包是穿过它们的平面。

凸集

如果集合$C$中任意两点间的线段仍然在$C$中，则称集合$C$为凸集。即对于$\forall x_1,x_2\in C$和$\theta\in[0,1]$都有

$$\theta x_1+(1-\theta)x_2\in C.$$
类似，我们称$\theta_1x_1+\cdots +\theta_kx_k$为$x_1,\cdots,x_k$的凸组合，其中$\theta_1+\cdots +\theta_k=1$，且$\theta_i\geqslant 0,i=1,\cdots,k$。一个凸集包含集合内所有点的凸组合。
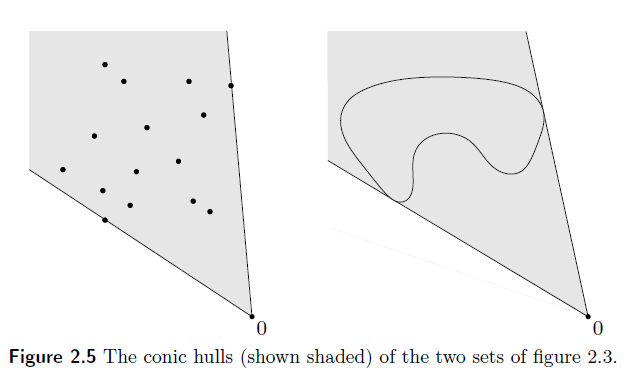
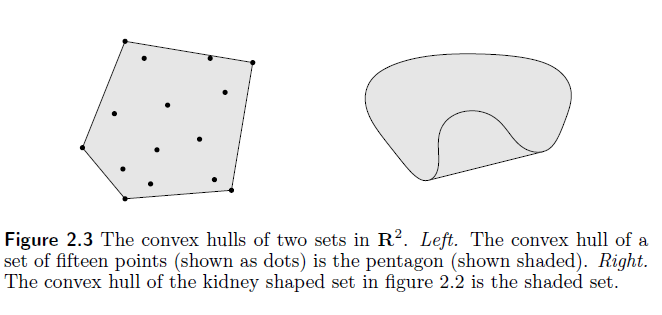
我们称集合$C$中所有点的凸组合组成的集合为集合$C$的凸包，记为$\textbf{conv}C$,
$$\textbf{conv}C=\{\theta_1x_1+\cdots+\theta_kx_k|x_i\in C,\theta_i\geqslant0,\theta_1+\cdots+\theta_k=1 \}.$$
凸包总是凸的，是包含$C$的最小凸集。

凸组合的概念可以推广到无穷级数、积分以及大多数形式的概率分布。比如，假设$\theta_1,\theta_2,\cdots$满足

$$\theta_i\geqslant0,i=1,2,\cdots,\quad\sum_{i=1}^\infty\theta_i=1,$$
且$x_1,x_2,\cdots\in C$，$C$为凸集。这时，如果级数$\sum_{i=1}^n\theta_ix_i$收敛，我们就有
$$\sum_{i=1}^n\theta_ix_i\in C.$$
更一般地，假设$p:\mathbf{R}^n\rightarrow\mathbf{R}$为定义在$C$上的概率密度。那么，如果积分$\int_Cp(x)xdx$存在，我们就有
$$\int_Cp(x)xdx\in C$$

锥

如果对于$\forall x\in C$和$\theta\geqslant 0$都有$\theta x\in C$，我们就称集合$C$是锥或者非负齐次。如果对于$\forall x_1,x_2\in C$和$\theta_1,\theta_2\geqslant 0$，都有

$$\theta_1x_1+\theta_2x_2\in C,$$
我们就称$C$为凸锥。
在二维平面上，具有此类形式的点构成一个以0为起点的扇形。

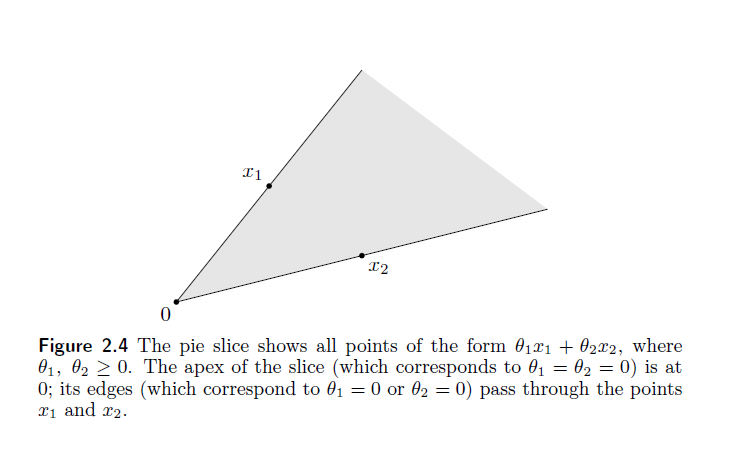
具有$\theta_1x_1+\cdots+\theta_kx_k,\theta_1,\cdots,\theta_k\geqslant0$形式的点称为$x_1,\cdots,x_k$的锥组合。和仿射(凸)组合一样，锥组合也可以推广到无穷级数和积分。
集合$C$的锥包是$C$中所有元素的锥组合的集合，即

$$\{\theta_1x_1+\cdots+\theta_kx_k|x_i\in C,\theta_i \geqslant0,i=1,\cdots,k\}$$
锥包是包含的最小的凸锥。