在 △ A B C \triangle ABC △ABC 中, M M M 为弧 B C BC BC (不含点 A A A) 的中点. 过外心 O O O 作 A B AB AB, A C AC AC 的垂线, 分别交以 A M AM AM 为直径的圆于点 P P P, Q Q Q. 设 P Q PQ PQ 与 A M AM AM 的中垂线交于点 R R R. 求证: A R / / B C AR//BC AR//BC.

证明:

设点 O O O 在 A C AC AC, A B AB AB 上的投影点分别为 O B O_B OB, O C O_C OC. 设 A M AM AM 中点为 E ( E ( E( 显然其为 ( A P Q ) (APQ) (APQ) 的圆心). 作出以 O A OA OA, O M OM OM 为直径的两圆 c 1 c_1 c1, c 2 c_2 c2, 设前者交 ( A P Q ) (APQ) (APQ) 于 A A A, K K K, 设后者交 ( A P Q ) (APQ) (APQ) 于 M M M, L L L.
显然, A A A, K K K, O C O_C OC, O O O, E E E, O B O_B OB 在 c 1 c_1 c1 上, L L L, M M M, E E E, O O O 在 c 2 c_2 c2 上.
∠ A K O = ∠ A K M = π 2 \angle AKO=\angle AKM=\frac{\pi}{2} ∠AKO=∠AKM=2π, 所以 M M M, O O O, K K K 共线.
同理, A A A, O O O, L L L 共线.
由根心定理, O E OE OE, A K AK AK, L M LM LM 三线共点, 记为 R ′ R' R′.
显然, A K / / B C AK//BC AK//BC.
若能证明 P P P, Q Q Q, E E E, O O O 共圆, 则由根心定理, P Q PQ PQ 也过 E O EO EO, L M LM LM 的交点, 即 R ′ R' R′. R R R 和 R ′ R' R′ 都是 O E OE OE 中垂线与 P Q PQ PQ 的交点, R R R 即 R ′ R' R′, 进而 A R / / B C AR//BC AR//BC. 下面证明: P P P, Q Q Q, E E E, O O O 共圆.
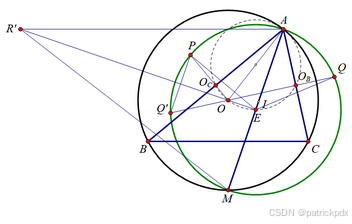
延长 Q O QO QO 交 ( A P Q ) (APQ) (APQ) 于点 Q ′ Q' Q′.
∠ P Q R ′ = E A O C = A / 2 \angle PQR'=EAO_C=A/2 ∠PQR′=EAOC=A/2, ∠ Q O E = ∠ E A O B = A / 2 \angle QOE=\angle EAO_B=A/2 ∠QOE=∠EAOB=A/2.
∠ Q ′ O R ′ = ∠ Q O E = A / 2 = ∠ P O R ′ \angle Q'OR'=\angle QOE=A/2=\angle POR' ∠Q′OR′=∠QOE=A/2=∠POR′. 显然, O E OE OE 是 ( A P Q ) (APQ) (APQ) 的一条对称轴, 由此易知 P P P, Q ′ Q' Q′ 关于 O E OE OE 对称.
∠ P E O = 2 ∠ P Q ′ Q = 2 ( π 2 − A / 2 ) = π − A = ∠ P O Q \angle PEO=2\angle PQ'Q=2(\frac{\pi}{2}-A/2)=\pi-A=\angle POQ ∠PEO=2∠PQ′Q=2(2π−A/2)=π−A=∠POQ.
∴ P \therefore P ∴P, Q Q Q, E E E, O O O 共圆.
证毕.
完成时间: 2024/12/30

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








