A
1
A_{1}
A1,
B
1
B_{1}
B1,
C
1
C_{1}
C1 分别是
△
A
B
C
\triangle ABC
△ABC 三边
B
C
BC
BC,
C
A
CA
CA,
A
B
AB
AB 上的点,
△
A
B
1
C
1
\triangle AB_{1} C_{1}
△AB1C1,
△
B
C
1
A
1
\triangle BC_{1} A_{1}
△BC1A1,
△
C
A
1
B
1
\triangle CA_{1} B_{1}
△CA1B1 的外接圆与
△
A
B
C
\triangle ABC
△ABC 的外接圆分别交于另一点
A
2
A_{2}
A2,
B
2
B_{2}
B2,
C
2
C_{2}
C2.
A
3
A_{3}
A3,
B
3
B_{3}
B3,
C
3
C_{3}
C3 分别是
A
1
A_{1}
A1,
B
1
B_{1}
B1,
C
1
C_{1}
C1 关于边
B
C
BC
BC,
C
A
CA
CA,
A
B
AB
AB 的中点的对称点. 求证:
△
A
2
B
2
C
2
∼
△
A
3
B
3
C
3
\triangle A_{2} B_{2} C_{2} \sim \triangle A_{3} B_{3} C_{3}
△A2B2C2∼△A3B3C3.
证明:
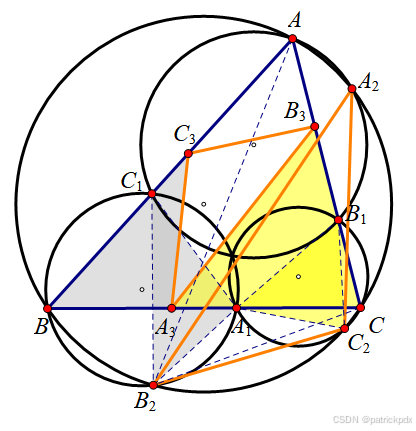
显然, △ B 2 C 1 A ∼ △ B 2 A 1 C \triangle B_2C_1A \sim \triangle B_2A_1C △B2C1A∼△B2A1C.
∴ B 2 C 1 / B 2 A 1 = A C 1 / C A 1 = B C 3 / B A 3 \therefore B_2C_1/B_2A_1=AC_1/CA_1=BC_3/BA_3 ∴B2C1/B2A1=AC1/CA1=BC3/BA3.
∠ C 1 B 2 A 1 = ∠ A B C \angle C_1B_2A_1=\angle ABC ∠C1B2A1=∠ABC.
∴ △ C 1 B 2 A 1 ∼ △ C 3 B A 3 \therefore \triangle C_1B_2A_1 \sim \triangle C_3BA_3 ∴△C1B2A1∼△C3BA3.
可类似地证明 △ B 1 C 2 A 1 ∼ △ B 1 C A 1 \triangle B_1C_2A_1 \sim \triangle B_1CA_1 △B1C2A1∼△B1CA1.
∠ B 2 B C = ∠ B 2 C 1 A 1 = ∠ B C 3 A 3 \angle B_2BC=\angle B_2C_1A_1=\angle BC_3A_3 ∠B2BC=∠B2C1A1=∠BC3A3.
∠ C 2 C A 1 = ∠ C 2 B 1 A 1 = ∠ C B 3 A 3 \angle C_2CA_1=\angle C_2B_1A_1=\angle CB_3A_3 ∠C2CA1=∠C2B1A1=∠CB3A3.
易知 ∠ B 2 A 2 C 2 = ∠ B C 3 A 3 + ∠ C B 3 A 3 − ∠ B A C \angle B_2A_2C_2=\angle BC_3A_3+\angle CB_3A_3-\angle BAC ∠B2A2C2=∠BC3A3+∠CB3A3−∠BAC.
∠ C 3 A 3 B 3 = ∠ B C 3 A 3 + ∠ C B 3 A 3 − ∠ B A C \angle C_3A_3B_3=\angle BC_3A_3+\angle CB_3A_3-\angle BAC ∠C3A3B3=∠BC3A3+∠CB3A3−∠BAC.
∴ \therefore ∴ ∠ B 2 A 2 C 2 = ∠ B 3 A 3 A 3 \angle B_2A_2C_2=\angle B_3A_3A_3 ∠B2A2C2=∠B3A3A3.
类似地, 可以证明 ∠ B 2 C 2 A 2 = ∠ B 3 C 3 A 3 \angle B_2C_2A_2=\angle B_3C_3A_3 ∠B2C2A2=∠B3C3A3.
∴ \therefore ∴ △ A 2 B 2 C 2 ∼ △ A 3 B 3 A 3 \triangle A_2B_2C_2 \sim \triangle A_3B_3A_3 △A2B2C2∼△A3B3A3.
2025年1月6日
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
